TTS Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 62: | Linia 62: | ||
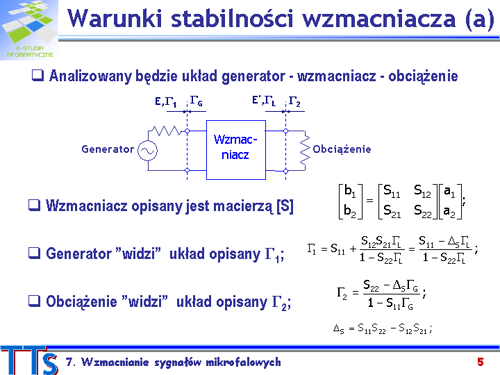
Natomiast obciążenie ”widzi” źródło o parametrach <math>E'\,</math> i <math>\Gamma_2\,</math>, przy czym najistotniejsza jest wartość współczynnika odbicia <math>\Gamma_2\,</math>. | Natomiast obciążenie ”widzi” źródło o parametrach <math>E'\,</math> i <math>\Gamma_2\,</math>, przy czym najistotniejsza jest wartość współczynnika odbicia <math>\Gamma_2\,</math>. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M7_Slaj6.png]] | |||
|valign="top"|Warunki stabilności są istotne przy projektowaniu układów wzmacniaczy. Rozpatrując je przyjmujemy, że oznacza, że wzmacniacz-dwuwrotnik nie jest otoczony elementami aktywnymi, które więcej odbijają, niż na nie pada. Jeśli tak jest, to wzmacniacz stabilny bezwarunkowo nie staje się aktywne z żadnej strony. | |||
Analizując warunki stabilności wprowadzono współczynnik stabilności K, wiążący ze sobą rozmaite współczynniki macierzy rozproszenia: | |||
Ilustracja warunków stabilności pokazana jest na rysunku. Ilustrowany jest warunek opisujący zachowanie współczynnika odbicia <math>\Gamma_1\,</math>. Transformujemy okrąg <math>|\Gamma_L| | |||
\le 1</math> z płaszczyzny <math>\Gamma_L\,</math> na płaszczyznę <math>\Gamma_1\,</math> – rysunek a). Dwuwrotnik jest stabilny bezwarunkowo, gdy przetransformowany okrąg leży wewnątrz okręgu jednostkowego – rysunek b). Gdy część przetransformowanego okręgu przekracza granicę okręgu jednostkowego – rysunek c), mamy do czynienia ze stabilnością warunkową. | |||
Wykazano, że warunkiem koniecznym i wystarczającym bezwarunkowej stabilności jest aby pewna kombinacja współczynników macierzy rozproszenia tranzystora spełniała następujący warunek <math>K>1\,</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M7_Slaj7.png]] | |||
|valign="top"|'''Wzmocnienie mocy''' dwuwrotnika/wzmacniacza <math>G\,</math> definiowane jest jako stosunek mocy <math>P_L\,</math> wydzielonej w obciążeniu do mocy <math>P_G\,</math> dostarczonej z generatora do obwodu: | |||
Otrzymana zależność nie jest łatwa w interpretacji. Widać, że w liczniku otrzymanego wyrażenia decydującą rolę pełni S21, ale także widać wpływ innych parametrów. Aby ocenić ich wpływ trzeba rozważania prowadzić dalej. | |||
Wersja z 13:30, 22 sie 2006
| Plik:TTS M7 Slaj6.png | Warunki stabilności są istotne przy projektowaniu układów wzmacniaczy. Rozpatrując je przyjmujemy, że oznacza, że wzmacniacz-dwuwrotnik nie jest otoczony elementami aktywnymi, które więcej odbijają, niż na nie pada. Jeśli tak jest, to wzmacniacz stabilny bezwarunkowo nie staje się aktywne z żadnej strony.
Analizując warunki stabilności wprowadzono współczynnik stabilności K, wiążący ze sobą rozmaite współczynniki macierzy rozproszenia: Ilustracja warunków stabilności pokazana jest na rysunku. Ilustrowany jest warunek opisujący zachowanie współczynnika odbicia . Transformujemy okrąg z płaszczyzny na płaszczyznę – rysunek a). Dwuwrotnik jest stabilny bezwarunkowo, gdy przetransformowany okrąg leży wewnątrz okręgu jednostkowego – rysunek b). Gdy część przetransformowanego okręgu przekracza granicę okręgu jednostkowego – rysunek c), mamy do czynienia ze stabilnością warunkową. Wykazano, że warunkiem koniecznym i wystarczającym bezwarunkowej stabilności jest aby pewna kombinacja współczynników macierzy rozproszenia tranzystora spełniała następujący warunek |
| Plik:TTS M7 Slaj7.png | Wzmocnienie mocy dwuwrotnika/wzmacniacza definiowane jest jako stosunek mocy wydzielonej w obciążeniu do mocy dostarczonej z generatora do obwodu:
Otrzymana zależność nie jest łatwa w interpretacji. Widać, że w liczniku otrzymanego wyrażenia decydującą rolę pełni S21, ale także widać wpływ innych parametrów. Aby ocenić ich wpływ trzeba rozważania prowadzić dalej. |