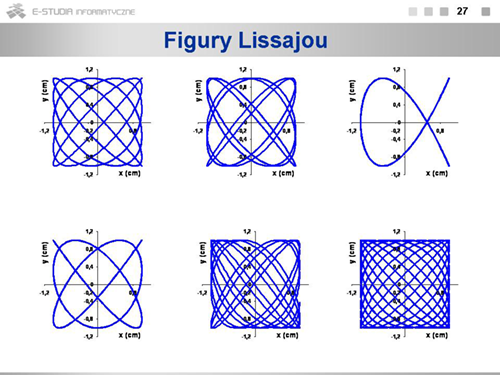
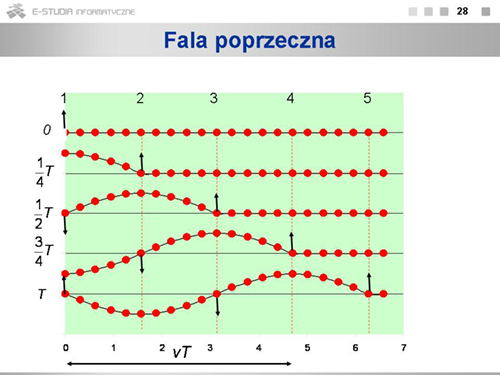
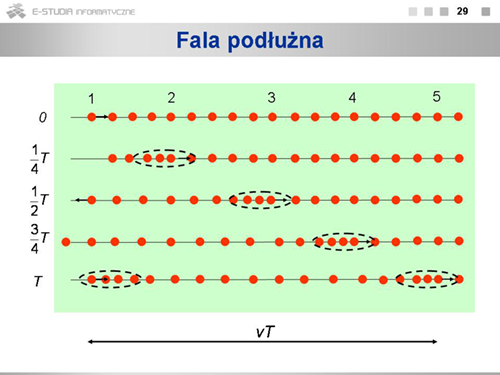
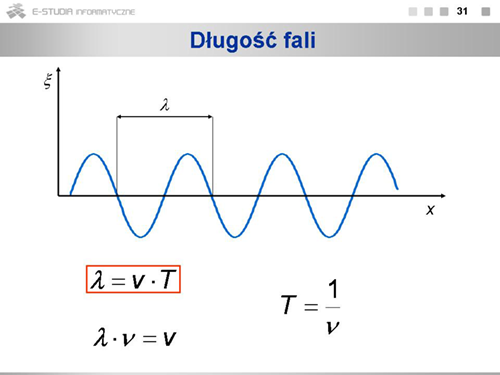
PF Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 363: | Linia 363: | ||
Szczególnym przypadkiem jest nakładanie się fali biegnącej i fali odbitej od jakiejś przeszkody. Powstaje wtedy fala stojąca. Niech <math>\xi_1=a cos (\omega t -kx)</math> oznacza falę biegnącą w prawo, a <math>\xi_1=a cos (\omega t +kx)</math> falę odbitą rozchodzącą się w lewo. Wybraliśmy tu taką chwilę początkową <math>(t=0)</math>, aby faza początkowa była równa zeru <math>(\varphi=0)</math>. Wychylenie dowolnego punktu z położenie równowagi <math>\xi\,</math> jest sumą wychyleń <math>\xi_1+\xi_2</math> . | Szczególnym przypadkiem jest nakładanie się fali biegnącej i fali odbitej od jakiejś przeszkody. Powstaje wtedy fala stojąca. Niech <math>\xi_1=a cos (\omega t -kx)</math> oznacza falę biegnącą w prawo, a <math>\xi_1=a cos (\omega t +kx)</math> falę odbitą rozchodzącą się w lewo. Wybraliśmy tu taką chwilę początkową <math>(t=0)</math>, aby faza początkowa była równa zeru <math>(\varphi=0)</math>. Wychylenie dowolnego punktu z położenie równowagi <math>\xi\,</math> jest sumą wychyleń <math>\xi_1+\xi_2</math> . | ||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd41.png]] | |||
|valign="top"|Po skorzystaniu ze wzoru na sumę cosinusów, otrzymujemy wyrażenie opisujące drgania z częstością kołową równą częstości drgań składowych <math>\omega\,</math>. Amplituda tych drgań jest zależna od położenia <math>x\,</math>, zmienia się sinusoidalnie od zera do maksymalnej wartości <math>2a\,</math> . W punktach, których współrzędna <math>x\,</math> spełnia warunek: <math>kx=\pm \left(n+\frac{1}{2} \right)\pi</math> , gdzie <math>n =0, 1, 2,...,\,</math> amplituda wynosi zero. Oznacza to, że te punkty cały czas pozostają w spoczynku. Miejsca takie nazywamy węzłami fali stojącej. Współrzędne węzłów wynoszą: <math>x_w=\pm \left(n+\frac{1}{2} \right)\frac{\lambda}{2}</math> . Natomiast punkty, dla których <math>kx=\pm n\pi</math> , drgają z maksymalną amplitudą. To są strzałki fali. Współrzędne strzałek mają wartości: <math>x_{strz}=\pm n\frac{\lambda}{2}</math> | |||
Wersja z 08:02, 21 sie 2006

|

|
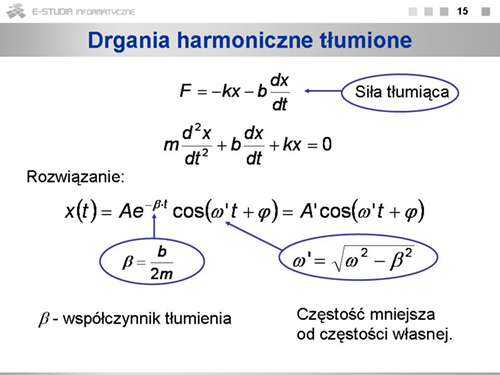
Sprawdźmy, czy nasze równanie będzie spełnione przez funkcję , gdzie , i są dowolnymi parametrami. Obliczamy pierwszą i drugą pochodną wychylenia po czasie i podstawiamy do równania. |

|
Okres i częstotliwość drgań
Okresem nazywamy czas jednego pełnego drgania. Po upływie okresu drgające ciało jest znów w takiej samej fazie. Okres powiązany jest z częstością wzorem: |

|
Prędkość i przyspieszenie
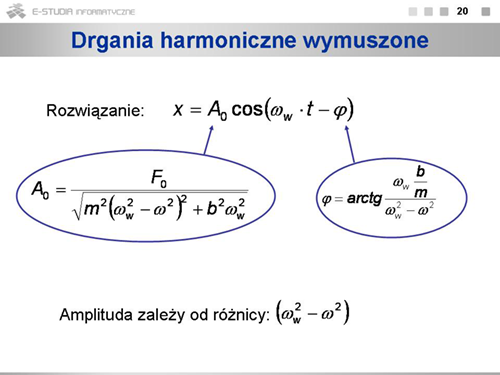
Prędkość i przyspieszenie w ruchu harmonicznym obliczamy jako pierwszą i drugą pochodną wychylenia po czasie. |

|
Energię kinetyczną w ruchu harmonicznym obliczamy, podstawiając do wzoru na energię kinetyczną prędkość w postaci . |
|
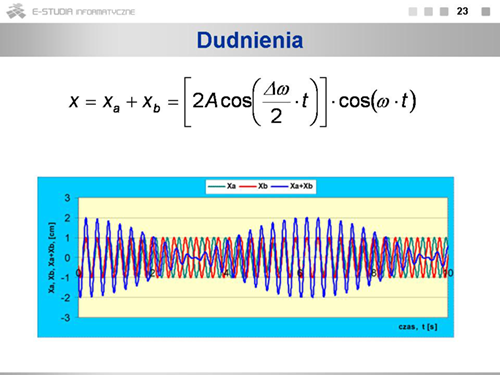
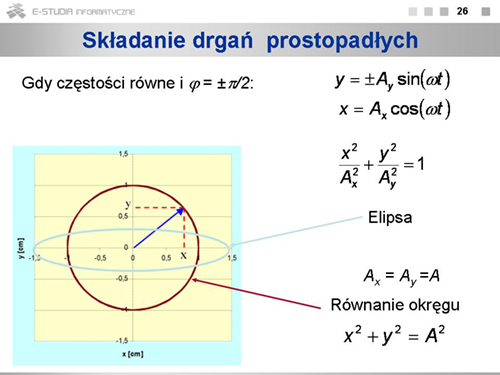
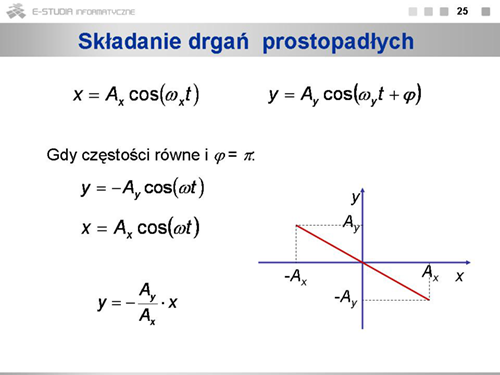
Jeśli częstości drgań są jednakowe i różnica faz wynosi , to ruch będzie ruchem harmonicznym wzdłuż prostej o równaniu . |

|
Po uwzględnieniu, że równanie falowe przybiera postać: |