PF Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 319: | Linia 319: | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd35.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd35.png]] | ||
|valign="top"|Oczywiście równanie fali płaskiej rozchodzącej się w kierunku malejących wartości <math>x\,</math>, otrzymamy zmieniając znak przy <math>x\,</math>. W przypadku, gdy ośrodek pochłania energię fali, amplituda drgań maleje wykładniczo: <math>a=a_0 e^{-\beta x}</math> . Drgania w miarę wzrostu <math>x\,</math> odbywają się z coraz mniejszą amplitudą, aż fala praktycznie zaniknie. | |valign="top"|Oczywiście równanie fali płaskiej rozchodzącej się w kierunku malejących wartości <math>x\,</math>, otrzymamy zmieniając znak przy <math>x\,</math>. W przypadku, gdy ośrodek pochłania energię fali, amplituda drgań maleje wykładniczo: <math>a=a_0 e^{-\beta x}</math> . Drgania w miarę wzrostu <math>x\,</math> odbywają się z coraz mniejszą amplitudą, aż fala praktycznie zaniknie. | ||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd36.png]] | |||
|valign="top"|Jeśli fala rozchodzi się w ośrodku jednorodnym i izotropowym, a źródło fali jest punktowe, to rozchodząca się fala jest falą kulistą. Równanie fali kulistej jest podobne do równania fali płaskiej – musimy współrzędną <math>x\,</math> zastąpić odległością od źródła fali <math>r\,</math>. Jest jednak pewna różnica. Amplituda fali kulistej, nawet w przypadku braku tłumienia, maleje wraz z odległością <math>r\,</math> wynosi <math>a/r\,</math> , gdzie <math>a\,</math> to amplituda drgań źródła fali. Jest to związane z faktem, że powierzchnie falowe fali kulistej są coraz większe w miarę rozchodzenia się fali. Energia drgającego punktu, źródła fali, musi być rozłożona na coraz więcej drgających punktów na powierzchniach falowych, a więc amplitudy drgań muszą maleć z <math>r\,</math>. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd37.png]] | |||
|valign="top"|'''Równanie falowe''' | |||
Równanie ruchu harmonicznego <math>x(t)=A cos(\omega t+\varphi)</math> otrzymaliśmy rozwiązując równanie różniczkowe wyrażające II zasadę dynamiki: <math>\frac{d^2 x}{dt^2}=-\frac{k}{m}x</math> . Jaka jest postać równania, którego rozwiązaniem jest równanie fali płaskiej? Domyślamy się, że powinno to być również równanie różniczkowe drugiego rzędu, symetryczne względem <math>x\,</math> i <math>t\,</math>. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd38.png]] | |||
|valign="top"|Aby znaleźć równanie falowe, obliczmy drugie pochodne cząstkowe po współrzędnej <math>x\,</math> i po czasie <math>t\,</math>. Dzieląc otrzymane wyrażenia odpowiednio przez <math>-\omega^2\,</math> i <math>-k^2\,</math> , otrzymujemy po prawej stronie identyczną wielkość <math>\xi\,</math> . Wobec tego możemy przyrównać lewe strony do siebie i otrzymujemy poszukiwane równanie falowe. | |||
Wersja z 07:36, 21 sie 2006

|

|
Sprawdźmy, czy nasze równanie będzie spełnione przez funkcję , gdzie , i są dowolnymi parametrami. Obliczamy pierwszą i drugą pochodną wychylenia po czasie i podstawiamy do równania. |

|
Okres i częstotliwość drgań
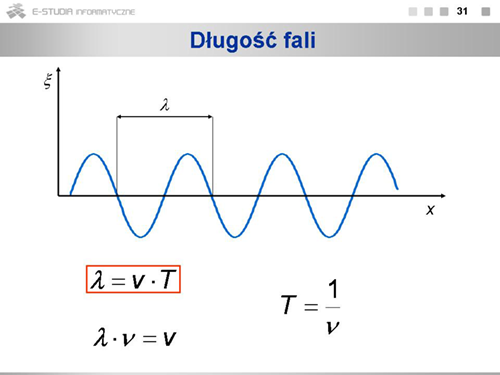
Okresem nazywamy czas jednego pełnego drgania. Po upływie okresu drgające ciało jest znów w takiej samej fazie. Okres powiązany jest z częstością wzorem: |

|
Prędkość i przyspieszenie
Prędkość i przyspieszenie w ruchu harmonicznym obliczamy jako pierwszą i drugą pochodną wychylenia po czasie. |

|
Energię kinetyczną w ruchu harmonicznym obliczamy, podstawiając do wzoru na energię kinetyczną prędkość w postaci . |
|
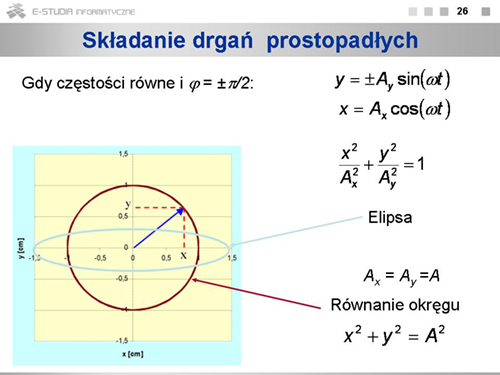
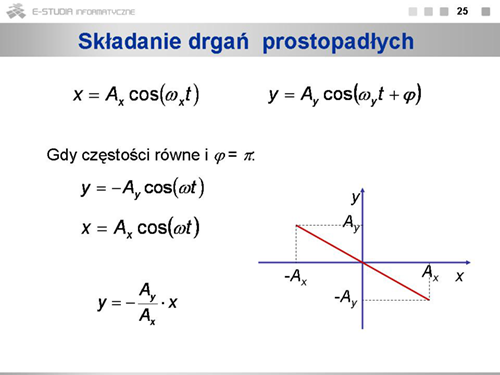
Jeśli częstości drgań są jednakowe i różnica faz wynosi , to ruch będzie ruchem harmonicznym wzdłuż prostej o równaniu . |