PF Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 302: | Linia 302: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd33.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd33.png]] | ||
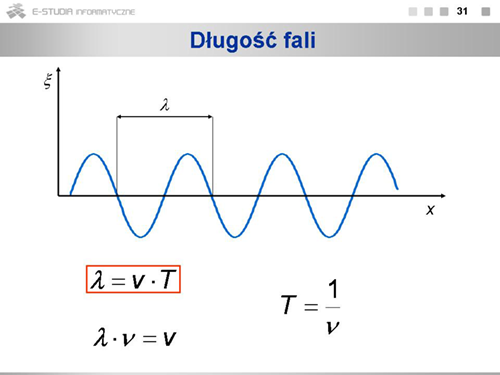
|valign="top"|Argument funkcji cosinus nazywamy fazą. Z jaką prędkością przesuwa się dana wartość fazy? Wyrażenie: <math>\omega\left(t-\frac{x}{v} \right) +\varphi=const</math> wiąże wartości <math>x\,</math> i <math>t\,</math>, dla których faza ma daną wartość. Po zróżniczkowaniu tego wyrażenia otrzymujemy: <math>v=\frac | |valign="top"|Argument funkcji cosinus nazywamy fazą. Z jaką prędkością przesuwa się dana wartość fazy? Wyrażenie: <math>\omega\left(t-\frac{x}{v} \right) +\varphi=const</math> wiąże wartości <math>x\,</math> i <math>t\,</math>, dla których faza ma daną wartość. Po zróżniczkowaniu tego wyrażenia otrzymujemy: <math>v=\frac{dx}{dt}</math> . Prędkość v nazywamy prędkością fazową, bo jest to prędkość przemieszczania się fazy. | ||
Wersja z 07:18, 21 sie 2006

|

|
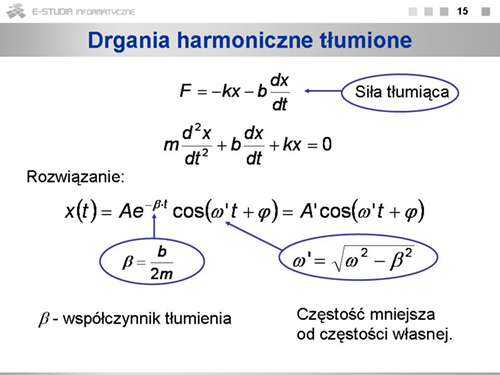
Sprawdźmy, czy nasze równanie będzie spełnione przez funkcję , gdzie , i są dowolnymi parametrami. Obliczamy pierwszą i drugą pochodną wychylenia po czasie i podstawiamy do równania. |

|
Okres i częstotliwość drgań
Okresem nazywamy czas jednego pełnego drgania. Po upływie okresu drgające ciało jest znów w takiej samej fazie. Okres powiązany jest z częstością wzorem: |

|
Prędkość i przyspieszenie
Prędkość i przyspieszenie w ruchu harmonicznym obliczamy jako pierwszą i drugą pochodną wychylenia po czasie. |

|
Energię kinetyczną w ruchu harmonicznym obliczamy, podstawiając do wzoru na energię kinetyczną prędkość w postaci . |
|
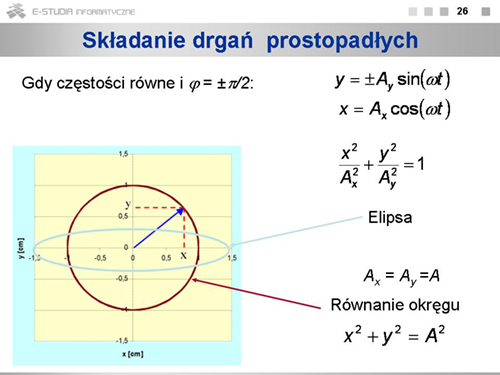
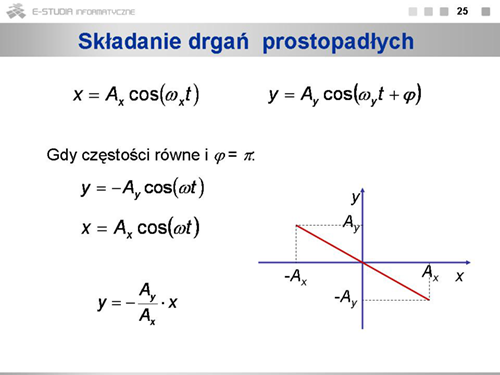
Jeśli częstości drgań są jednakowe i różnica faz wynosi , to ruch będzie ruchem harmonicznym wzdłuż prostej o równaniu . |