PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 176: | Linia 176: | ||
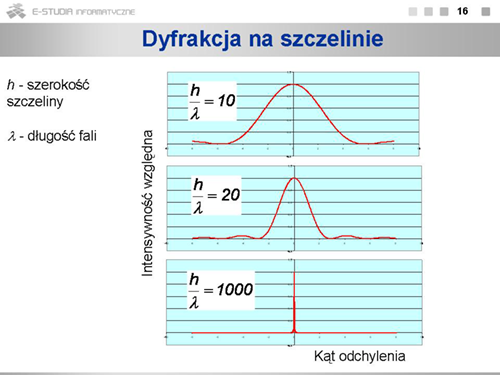
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd16.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd16.png]] | ||
|valign="top"|Warto zobaczyć, jak zmiana intensywności zależy od szerokości szczeliny i długości fali. Z postaci wzoru na <math>I_{wzgl}\,</math> widać, że zależy nie tyle od samych tych wartości, ale od ich stosunku <math>h/{\lambda}\,</math> . Szerokość głównego maksimum dyfrakcyjnego jest tym większa, im węższa jest szczelina. Gdy szerokość szczeliny jest dużo większa od długości fali (dolny wykres) zjawiska dyfrakcji, czyli ugięcia na szczelinie, praktycznie nie obserwujemy. | |valign="top"|Warto zobaczyć, jak zmiana intensywności zależy od szerokości szczeliny i długości fali. Z postaci wzoru na <math>I_{wzgl}\,</math> widać, że zależy nie tyle od samych tych wartości, ale od ich stosunku <math>h/{\lambda}\,</math> . Szerokość głównego maksimum dyfrakcyjnego jest tym większa, im węższa jest szczelina. Gdy szerokość szczeliny jest dużo większa od długości fali (dolny wykres) zjawiska dyfrakcji, czyli ugięcia na szczelinie, praktycznie nie obserwujemy. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd17.png]] | |||
|valign="top"|'''Złożenie interferencji i dyfrakcji''' | |||
Uzyskaliśmy interferencyjne efekty na pojedynczej szczelinie, zaś poprzednio rozważaliśmy układ dwóch szczelin, gdzie również określiliśmy warunki na wzmacnianie i wygaszanie wypadkowej fali interferencyjnej. Można się więc spodziewać, że w układzie dwóch szczelin, uzyskamy superpozycje obu dyskutowanych tu efektów. Przypomnijmy sobie wzór na falę, będącą rezultatem nałożenia się dwóch fal o tych samych częstościach i amplitudach. Uzyskujemy fale wypadkową, <math>y_{12}\,</math>, której amplituda zależy od różnicy faz fal składowych. W naszym przypadku możemy wzór na amplitudę zapisać następująco: | |||
: <math>E_i=2E_{0i}cos \left(\frac{\varphi_i}{2} \right)=E_m cos\alpha_i</math> | |||
gdzie przez <math>E_i\,</math> (i – od interferencji) oznaczyliśmy amplitudę fali zależną od różnicy faz promieni przechodzących przez dwie szczeliny, a przez <math>E_{0i}\,</math> amplitudę fali biegnącej z każdej szczeliny. Amplituda maksymalna <math>E_m\,</math> jest sumą obu amplitud składowych <math>E_m=2E_{0i}</math>. Podobnie jak w przypadku dyfrakcji <math>\alpha_i=\varphi_i /2</math>. Należy jeszcze powiązać różnicę faz z kątem odchylenia promieni od pierwotnego kierunku fali padającej na układ szczelin. Wykorzystamy tu otrzymaną dla pojedynczej szczeliny zależność <math>\alpha=\frac{\pi}{\lambda}h sin\theta</math> , gdzie zamiast szerokości szczeliny h wstawiamy odległość pomiędzy dwoma szczelinami <math>d\,</math> : <math>\alpha_i \frac{\pi d}{\lambda} sin\theta</math>. | |||
Natężenie fali (intensywność) jest proporcjonalna do kwadratu amplitudy. Intensywność obrazu interferencyjnego możemy więc zapisać w postaci: | |||
: <math>I_i=I_{mi}cos^2 \alpha_i</math> | |||
gdzie <math>I_{mi}\,</math> jest maksymalną intensywnością promieni biegnących z każdej szczeliny. | |||
Wersja z 20:02, 17 sie 2006

|
|
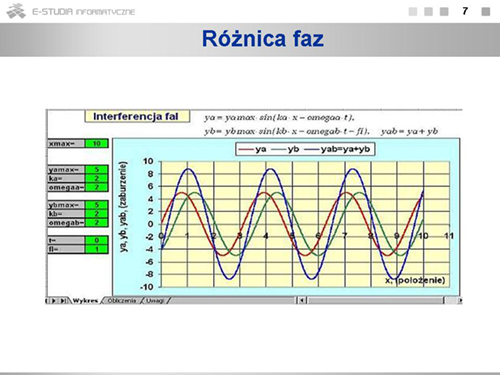
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |