PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 144: | Linia 144: | ||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd13.png]] | |width="450px" valign="top"|[[Grafika:PF_M16_Slajd13.png]] | ||
|valign="top"|Dla wyznaczenia sumarycznej fazy oraz amplitudy wypadkowej fali wykorzystamy tu metodę tak zwanych strzałek fazowych. Metoda ta umożliwia graficzne dodawanie wielkiej liczby fal o tej samej amplitudzie <math>E_0\,</math> i częstości <math>\omega\,</math>, a różniących się fazą. Ilustruje to rysunek. Niech pierwsza fala wynosi <math>E_1=E_0 sin(\omega t)</math> , kolejna - różniąca się od pierwszej przesunięciem w fazie o <math>\varphi\,</math> będzie <math>E_2=E_0 sin(\omega t+\varphi)</math>, kolejna niech będzie przesunięta o <math>2\varphi\,</math> itd. Każda strzałka reprezentuje falę o danej amplitudzie, której odpowiada długość strzałki. Faza fali określona jest przez kąt między osią x a kierunkiem strzałki. Wypadkową amplitudę i fazę otrzymujemy sumując wektorowo strzałki (kolejna strzałka ma swój początek w miejscu, gdzie kończy się poprzednia). Na rysunku pokazane są przykładowo różnymi kolorami cztery fale i ich złożenie pokazane kolorem czerwonym. | |valign="top"|Dla wyznaczenia sumarycznej fazy oraz amplitudy wypadkowej fali wykorzystamy tu metodę tak zwanych strzałek fazowych. Metoda ta umożliwia graficzne dodawanie wielkiej liczby fal o tej samej amplitudzie <math>E_0\,</math> i częstości <math>\omega\,</math>, a różniących się fazą. Ilustruje to rysunek. Niech pierwsza fala wynosi <math>E_1=E_0 sin(\omega t)</math> , kolejna - różniąca się od pierwszej przesunięciem w fazie o <math>\varphi\,</math> będzie <math>E_2=E_0 sin(\omega t+\varphi)</math>, kolejna niech będzie przesunięta o <math>2\varphi\,</math> itd. Każda strzałka reprezentuje falę o danej amplitudzie, której odpowiada długość strzałki. Faza fali określona jest przez kąt między osią x a kierunkiem strzałki. Wypadkową amplitudę i fazę otrzymujemy sumując wektorowo strzałki (kolejna strzałka ma swój początek w miejscu, gdzie kończy się poprzednia). Na rysunku pokazane są przykładowo różnymi kolorami cztery fale i ich złożenie pokazane kolorem czerwonym. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd14.png]] | |||
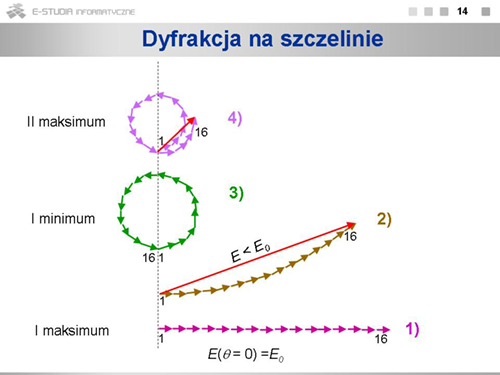
|valign="top"|W naszym przypadku fali przechodzącej przez szczelinę, sumaryczna amplituda i sumaryczna faza będzie złożeniem n składowych i zależeć będzie, zgodnie ze wzorem <math>\Delta \varphi=\frac{2\pi}{\lambda}\Delta h sin\theta</math> od kąta <math>\theta\,</math> określającego położenie danego punktu na ekranie względem szczeliny. | |||
Jeśli kąt ten jest równy zeru, czyli punkt obserwacji leży na wprost szczeliny, to i <math>\Delta \varphi</math> będzie równe zeru i sumaryczna amplituda będzie algebraiczną sumą <math>n\,</math> jednakowych składników. Jeśli kąt <math>\theta\,</math> będzie inny, musimy sumować <math>n\,</math> fal składowych zgodnie z metodą strzałek fazowych. Ilustruje to rysunek, gdzie <math>n=16\,</math>. Przypadek 1) odpowiada sytuacji, gdy <math>\theta=0</math>, a więc i różnica faz <math>\Delta \varphi=0</math>. Sumaryczna amplituda jest tu maksymalna, oznaczyliśmy ją <math>E_0\,</math>. Kolejne przypadki 2), 3) i 4) odpowiadają wzrastającej wartości kąta obserwacji <math>\theta\,</math>. Przypadek 2) ilustruje sytuację, gdy <math>\theta\,</math> nieco większe od zera. Suma algebraiczna wszystkich 16 składników (długość łuku) jest taka sama, jak poprzednio, równa <math>E_0\,</math>, ale wypadkowa amplituda (wartość sumy wektorowej) jest mniejsza od <math>E_0\,</math>. W przypadku 3) sumaryczna amplituda wynosi zero, czyli będzie to pierwsze minimum. Przy dalszym wzroście kąta <math>\theta\,</math> amplituda znów będzie różna od zera, ale jej wartość stanie się o wiele mniejsza. Liczba pasków, na które podzieliliśmy w myśli szczelinę może być dowolna. Im będzie większa, tym węższe będą paski, ale końcowe przesunięcie fazowe i zmiana amplitudy będą, dla danej długości fali, określone tylko wartością kąta odchylenia <math>\theta\,</math>. (Pomocniczy wskaźnik n przestaje więc być istotny i dalej potrzebny.) Związek pomiędzy wartością kąta <math>\theta\,</math>, a amplitudą wypadkowej fali możemy znaleźć rozpatrując zależności geometryczne zilustrowane na rysunku. | |||
Wersja z 19:26, 17 sie 2006

|
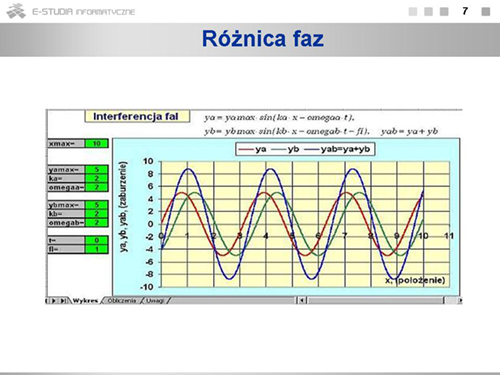
|
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |