PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 114: | Linia 114: | ||
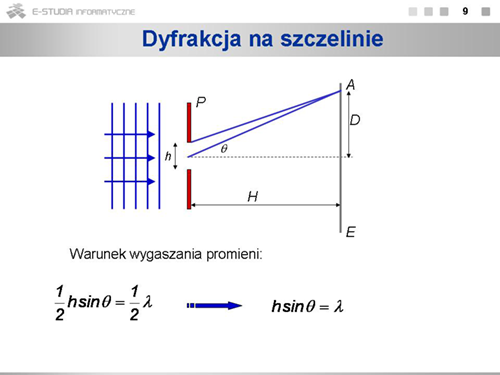
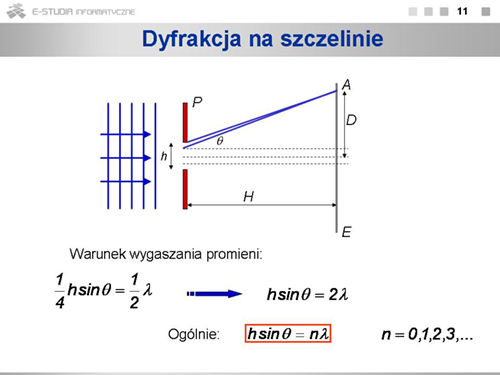
: <math>h sin\theta=n\lambda</math> , gdzie <math>n=1, 2, 3,...\,</math> | : <math>h sin\theta=n\lambda</math> , gdzie <math>n=1, 2, 3,...\,</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd12.png]] | |||
|valign="top"|Minimów i leżących pomiędzy nimi maksimów może więc być bardzo wiele. Powstaje pytanie, jaki będzie rozkład natężeń w obrazie dyfrakcyjnym, jak natężenie wypadkowej fali zależeć będzie od kąta odchylenia promieni od pierwotnego kierunku? Największe wzmocnienie natężenia fali uzyskujemy, gdy obie fale mają taką sama fazę, największe osłabienie, gdy faza jest przeciwna. Pomiędzy tymi skrajnymi przypadkami mamy wszystkie przypadki pośrednie, zależne od różnicy faz. | |||
Podzielmy w myśli całą szerokość szczeliny na n pasków. Ilustruje to rysunek obok, gdzie <math>n=5\,</math>. (Wskaźnik <math>n\,</math> odgrywa tu pomocniczą rolę i nie należy go mylić ani ze współczynnikiem załamania, ani z numeracją maksimów i minimów interferencyjnych.) Różnica faz <math>\Delta \varphi\,</math> dla fal biegnących od dwóch sąsiednich pasków zależy od różnicy dróg <math>\Delta r</math>, jak pokazano na rysunku. Kiedy różnica dróg równa jest długości fali, to odpowiadająca różnica faz równa jest <math>2\pi\,</math>. | |||
Mamy więc proporcję: | |||
<math>\frac{\Delta r}{\lambda}=\frac{\Delta \varphi}{2\pi}</math> czyli <math>\Delta \varphi=\frac{2\pi}{\lambda}\Delta r=\frac{2\pi}{\lambda}\Delta h sin\theta</math> | |||
Wersja z 19:04, 17 sie 2006

|
|
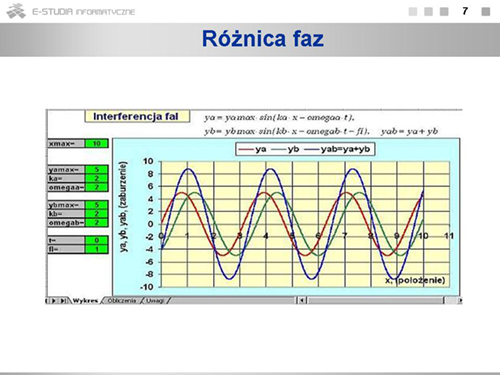
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |