PF Moduł 16: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 89: | Linia 89: | ||
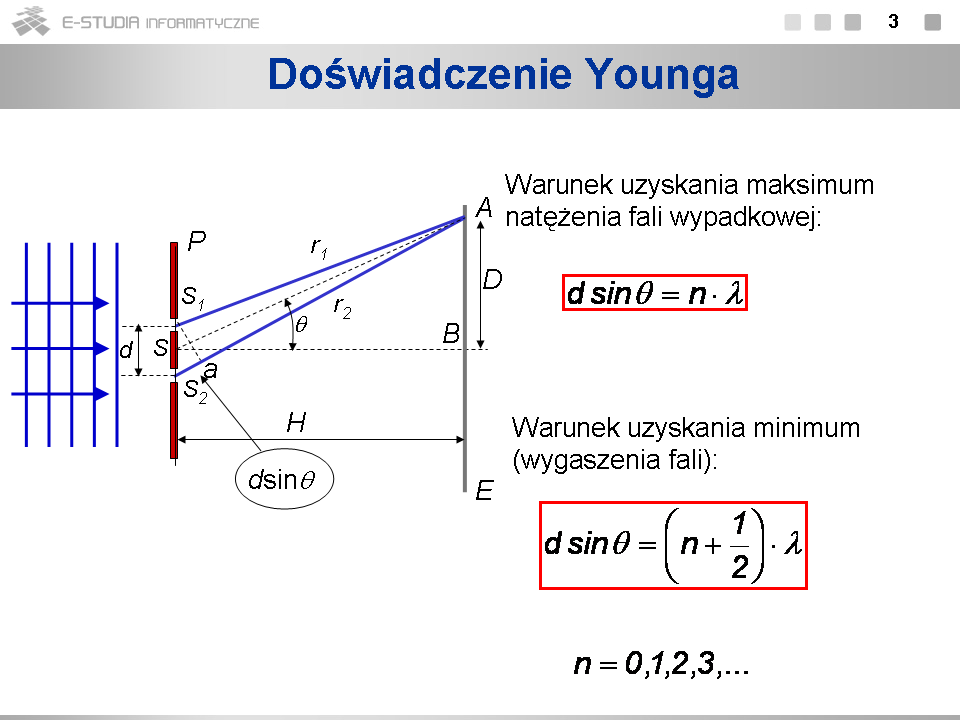
|valign="top"|Czy możliwa jest interferencja światła przechodzącego przez pojedynczą szczelinę lub otwór? Odruchowa odpowiedź jest - że nie, bo przechodzące światło nie ma z czym interferować. Zasada Hyghensa mówi jednak, że każdy punkt, do którego dochodzi fala staje się źródłem nowej fali kulistej. Fale pochodzące z różnych punktów szczeliny mogą więc także interferować. Kiedy szczelina jest bardzo szeroka, to w rezultacie tworzy się czoło fali płaskiej i efektu interferencji nie obserwujemy. Kiedy jednak rozmiary szczeliny stają się porównywalne z długością fali, efekt interferencji powinien być możliwy do zaobserwowania. Rzeczywiście, efekty takie się obserwuje i choć w swej naturze nie różnią się one od znanej nam już interferencji otrzymały inną nazwę - '''dyfrakcji''', czyli "uginania się" fal. | |valign="top"|Czy możliwa jest interferencja światła przechodzącego przez pojedynczą szczelinę lub otwór? Odruchowa odpowiedź jest - że nie, bo przechodzące światło nie ma z czym interferować. Zasada Hyghensa mówi jednak, że każdy punkt, do którego dochodzi fala staje się źródłem nowej fali kulistej. Fale pochodzące z różnych punktów szczeliny mogą więc także interferować. Kiedy szczelina jest bardzo szeroka, to w rezultacie tworzy się czoło fali płaskiej i efektu interferencji nie obserwujemy. Kiedy jednak rozmiary szczeliny stają się porównywalne z długością fali, efekt interferencji powinien być możliwy do zaobserwowania. Rzeczywiście, efekty takie się obserwuje i choć w swej naturze nie różnią się one od znanej nam już interferencji otrzymały inną nazwę - '''dyfrakcji''', czyli "uginania się" fal. | ||
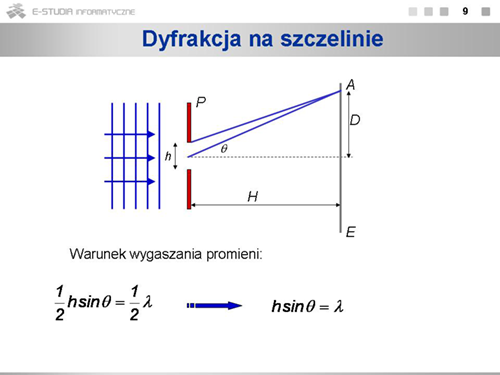
Na rysunku pokazano dwa przykładowe promienie, które będą z sobą interferować. Szerokość szczeliny oznaczamy symbolem <math>h\,</math>. Podobnie jak poprzednio, zakładamy, że <math>H>>h\,</math> i możemy uznać promienie biegnące z różnych punktów szczeliny za równoległe, co jest na ogół z niezłym przybliżeniem spełnione i upraszcza opis ilościowy. Taki przypadek nosi nazwę dyfrakcji Fraunhofera w odróżnieniu od dyfrakcji Fresnela, gdzie zakłada się, że odległość pomiędzy źródłem i ekranem ma skończoną wartość. Rozważmy na początek dwa promienie wybiegające z punktów szczeliny odległych o <math>h/2\,</math>. Warunek ich wygaszania się <math>\frac{h}{2}sin\=</math> dla n=0 (pierwsze minimum) wyraża się wzorem: | Na rysunku pokazano dwa przykładowe promienie, które będą z sobą interferować. Szerokość szczeliny oznaczamy symbolem <math>h\,</math>. Podobnie jak poprzednio, zakładamy, że <math>H>>h\,</math> i możemy uznać promienie biegnące z różnych punktów szczeliny za równoległe, co jest na ogół z niezłym przybliżeniem spełnione i upraszcza opis ilościowy. Taki przypadek nosi nazwę dyfrakcji Fraunhofera w odróżnieniu od dyfrakcji Fresnela, gdzie zakłada się, że odległość pomiędzy źródłem i ekranem ma skończoną wartość. Rozważmy na początek dwa promienie wybiegające z punktów szczeliny odległych o <math>h/2\,</math>. Warunek ich wygaszania się <math>\frac{h}{2}sin\theta=\left(n+\frac{1}{2} \right)\lambda</math> dla n=0 (pierwsze minimum) wyraża się wzorem: | ||
: <math>\frac{h}{2}sin\theta=\frac{1}{2} \right)\lambda</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd10.png]] | |||
|valign="top"|Na poprzednim rysunku rozważaliśmy jeden promień z górnego krańca szczeliny, drugi z jej środka. Możemy jednak przemieszczać się w dół z położeniami obu promieni odnajdując dla każdego promienia z górnej połowy szczeliny odpowiadający mu promień z połowy dolnej. Warunek na wygaszenie będzie dla tych przesuniętych promieni identyczny jak poprzednio. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M16_Slajd11.png]] | |||
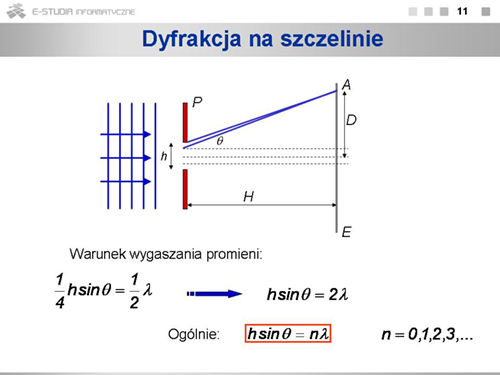
|valign="top"|Możliwe są i inne kombinacje. Gdyby odległość pomiędzy rozważanymi promieniami była równa jednej czwartej szerokości szczeliny, to warunek na wygaszanie byłby: | |||
: <math>\frac{1}{4}h sin\theta=\frac{1}{2} \right)\lambda</math> , czyli <math>h sin\theta=2\lambda</math> | |||
Uogólniając, można napisać, że warunek na wygaszanie się promieni biegnących z różnych punktów szczeliny ma postać: | |||
: <math>h sin\theta=n\lambda</math> , gdzie <math>n=1, 2, 3,...\,</math> | |||
Wersja z 15:09, 17 sie 2006

|
|
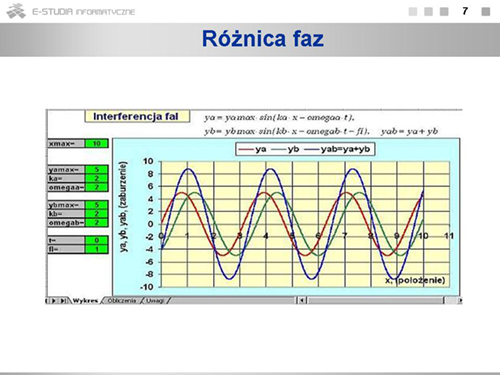
Kiedy inne parametry fal (na przykład częstość, amplituda) będą się różnić, fala wypadkowa nie musi być falą sinusoidalną. Możesz to sprawdzić sam, korzystając z załączonej ilustracji interaktywnej. |