PF Moduł 15: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 187: | Linia 187: | ||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd20.png]] | |width="450px" valign="top"|[[Grafika:PF1_M15_Slajd20.png]] | ||
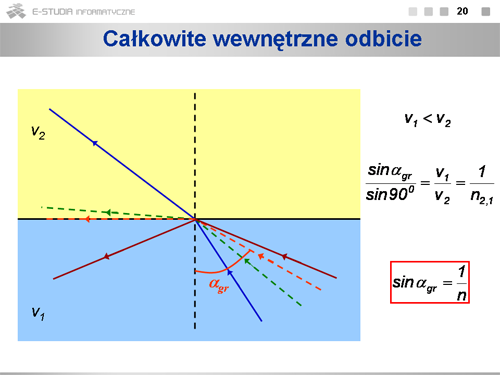
|valign="top"|Jeśli promień padający biegnie w ośrodku gęstszym optycznie (czyli <math>v_1<v_2</math>), to kąt załamania jest większy niż kąt padania. Zwiększając kąt padania dochodzimy do sytuacji, gdy kąt załamania równy jest <math>90^\circ\,</math>. Taki kąt padania nazywamy kątem granicznym. Sinus kąta granicznego jest odwrotnością współczynnika załamania ośrodka gęstszego optyczne względem ośrodka rzadszego optycznie. Jeśli światło padnie na granicę ośrodków pod kątem większym od granicznego, odbije się w całości od granicy. Jest to zjawisko całkowitego wewnętrznego odbicia. Wykorzystywane jest ono w konstrukcji światłowodów. | |valign="top"|Jeśli promień padający biegnie w ośrodku gęstszym optycznie (czyli <math>v_1<v_2</math>), to kąt załamania jest większy niż kąt padania. Zwiększając kąt padania dochodzimy do sytuacji, gdy kąt załamania równy jest <math>90^\circ\,</math>. Taki kąt padania nazywamy kątem granicznym. Sinus kąta granicznego jest odwrotnością współczynnika załamania ośrodka gęstszego optyczne względem ośrodka rzadszego optycznie. Jeśli światło padnie na granicę ośrodków pod kątem większym od granicznego, odbije się w całości od granicy. Jest to zjawisko całkowitego wewnętrznego odbicia. Wykorzystywane jest ono w konstrukcji światłowodów. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd21.png]] | |||
|valign="top"|'''Zasada Fermata''' | |||
Druga zasada, sformułowana przez Pierre'a Fermata w 1650 roku dotyczy czasu przejścia światła pomiędzy dwoma punktami. Jej sens można sformułować następująco. | |||
Światło biegnie po takiej drodze, na pokonanie której potrzebny jest ekstremalny (na ogół najmniejszy) czas. | |||
Zasada ta umożliwia na przykład sformułowanie praw odbicia i załamania fal poprzez znalezienie warunków minimalnego czasu na pokonanie drogi pomiędzy dwoma zadanymi punktami. | |||
Zasada Fermata jest szczególnym przypadkiem tzw. zasady wariacyjnej, według której dla rozwiązania danego zagadnienia poszukuje się takiej funkcji, dla której określona całka przyjmuje wartość ekstremalną. W naszych przykładach całką tą będzie sumaryczny czas. Zasada ta umożliwia rozwiązywanie wielu problemów nie tylko z dziedziny fizyki. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd22.png]] | |||
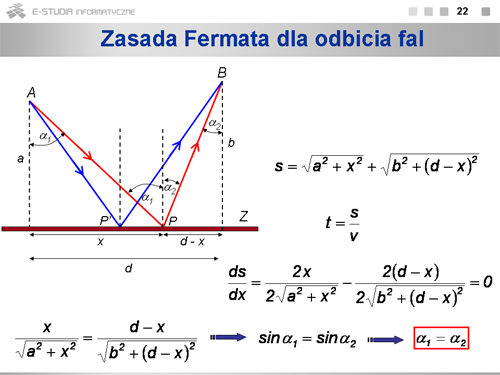
|valign="top"|Warunki geometryczne dla odbicia promieni świetlnych od granicy dwóch ośrodków pokazane są na rysunku. "Próbny" promień pokazany jest kolorem czerwonym. Ośrodek jest wciąż ten sam, więc światło porusza się cały czas z tą samą prędkością. Minimum czasu odpowiada więc najkrótszej drodze. Długość drogi pomiędzy punktami <math>A\,</math> i <math>B\,</math>, określonej tak, że promień świetlny musi w jakimś punkcie odbić się od zwierciadła <math>Z\,</math>, może być zapisana w postaci: <math>s=\sqrt{a^2+x^2}+\sqrt{b^2+(d-x)^2}</math>. Poszukujemy takiej wartości <math>x\,</math>, dla której droga <math>s\,</math> mieć będzie wartość minimalną. W tym celu obliczamy pochodną ds/dx i przyrównujemy ją do zera. Otrzymujemy: <math>\frac{x}{\sqrt{a^2+x^2}}=\frac{d-x}{\sqrt{b^2+(d-x)^2}}</math>, czyli <math>sin\alpha_1=sin\alpha_2</math>. Oznacza to, że kąt odbicia równy jest kątowi padania. Oba promienie padający i odbity oraz normalna leżą w jednej płaszczyźnie. Światło pobiegnie więc od punktu <math>A\,</math> do punktu <math>B\,</math> po takiej drodze, by spełniony był warunek minimalnego czasu, a wiec nie po drodze <math>APB\,</math>, ale <math>AP'B\,</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd23.png]] | |||
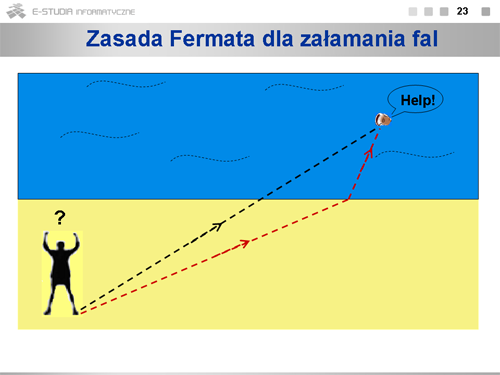
|valign="top"|Dla zjawiska odbicia mogliśmy zasadę najkrótszego czasu zastąpić zasadą najkrótszej drogi, bo prędkość światła przez cały czas była jednakowa. Inaczej jest, gdy światło przechodzi przez granicę dwóch ośrodków i jego prędkość zmienia się. Analogiczna sytuacja jest wtedy, gdy ratownik musi w najkrótszym czasie dotrzeć do wzywającego pomocy. Bez obliczania całek wybierze on taką drogę, aby jej większa część przypadła na plażę, gdzie porusza się znacznie szybciej niż w wodzie. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF1_M15_Slajd24.png]] | |||
|valign="top"|Zastosujmy zasadę Fermata do zjawiska załamania fali na granicy dwóch ośrodków o współczynnikach załamania <math>n_1\,</math> i <math>n_2\,</math>. Relacje geometryczne przedstawia rysunek. Pamiętając, że współczynnik załamania jest stosunkiem prędkości światła w próżni do prędkości w danym ośrodku <math>n=\frac{c}{v}</math>, otrzymujemy wyrażenie na czas przebycia przez światło drogi od <math>A\,</math> do <math>B\,</math>: <math>t=\frac{n_1 l_1+n_2 l_2}{c}</math>. Wielkość <math>l=n_1 l_1+n_2 l_2</math> nosi nazwę drogi optycznej. Poszukujemy więc takiej wartości <math>x\,</math>, przy ustalonych położeniach punktów <math>A\,</math> i <math>B\,</math>, by droga optyczna była minimalna. W tym celu obliczamy pochodną wyrażenia, w którym drogę optyczną określamy w funkcji <math>x\,</math>: <math>l=n_1\sqrt{a^2+x^2}+n_2\sqrt{b^2+(c-x)^2}</math>. Po przyrównaniu pochodnej <math>dl/dx\,</math> do zera otrzymujemy: <math>n_1\frac{x}{\sqrt{a^2+x^2}}=n_2\frac{c-x}{\sqrt{b^2+(c-x)^2}}</math>, czyli znane prawo załamania: <math>n_1 sin\alpha_1=n_2 sin\alpha_2</math>. | |||
Wersja z 11:48, 17 sie 2006

|

|
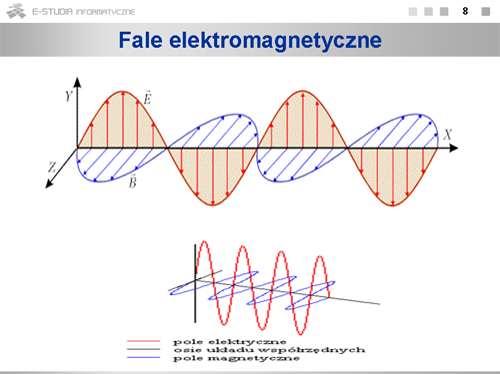
Nasze rozważania rozpoczniemy od przypomnienia równań Maxwella, które przedstawiają relacje pomiędzy zmianami pól: elektrycznego i magnetycznego w czasie i przestrzeni. |

|
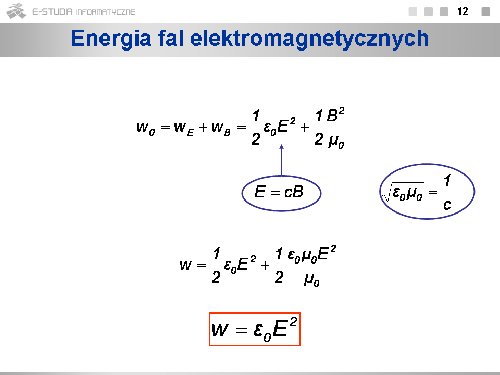
Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: lub . |