Algorytmy i struktury danych/Algorytmy tekstowe II

Algorytmy tekstowe II

Poprzednie algorytmy dokonywały jedynie na tekstach wejściowych operacji sprawdzania symboli na równość. Załóżmy teraz, że alfabet jest liniowo uporządkowany. Pokażemy, że porównywanie symboli w sensie porządku liniowego można istotnie wykorzystać w algorytmach tekstowych. Porządek liniowy na symbolach implikuje {\em porządek leksykograficzny} na słowach, na przykład:

$ab<ababab<abb<abbaa<abbaaaaaaaaaaa<abbaaaaaab$

Równoważność cykliczna grafów

Pokażemy problem, który prawdopodobie najlepiej pokazuje użyteczność porządku liniowego na alfabecie. Rotacją słowa $u=u[1..n]$ jest kaz'rde słowo postaci $u^{(k)}=u[k+1..n]u[1..k]$. (w szczególności $u^{(0)}=u^{(n)}=u)$. Niech $u,w$ będą słowami długości $n$, mówimy, że są one cyklicznie równoważne gdy $u^{(i)}=w^{(j)}$ dla pewnych $i,j$.

Naturalnym algorytmem sprawdzania cyklicznej równoważności jest szukanie słowa $u$ w słowie $ww$, ale podamy algorytm znacznie prostszy bazujący , który będzie działal w czasie liniowym i {\em w miejscu} (dodatkowa pamięć jest stała). W algorytmie roszerzamy teblicę $u,w$ na $uu,ww$ ale robimy to jedynie dla uproszczenia, w rzeczywistości możemy poruszać się cyklicznie po $u$ i po $w$, pozostawiamy modyfikację jako ćwiczenie.

Algorytm Równoważność-Cykliczna

---

$x:=uu$; $y:=ww$;
$i:=0$; $j:=0$;
while $(i<n)$ and $(j<n)$ do
   $k:=1$;
   while$x[i+k]=y[j+k]$ do $k:=k+1$;
   if $k>n$ then return true;
   if $x[i+k]>y[i+k]$ then$i:=i+k$ else $j:=j+k$;
return false;

Zdefiniujmy:

$D(u)=\{k:1\le k\le n$ oraz $u^{(k)}>w^{(j)}$ dla pewnego $j\}$,
$D(w)=\{k:1\le k\le n$ oraz $w^{(k)}>u^{(j)}$ dla pewnego $j\}$.

Skorzystamy z prostego faktu: Jeśli $D(u)=[1..n]$ lub $D(w)=[1..n]$, to $u,w$ nie są równoważne.

Uzasadnienie pozostawiamy jako ćwiczenie. Poprawność algorytmu wynika teraz z tego, że po każdej głównej iteracji zachodzi niezmiennik:

$D(w)\supseteq [1..i]$\ oraz \ $D(u)\supseteq [1..j]$.

Liczba porównań jest oczywiście liniowa. Pozostawiamy jako ćwiczenie policzenie dokładnego wzoru na maksymalną liczbę porównań symboli dla tekstów długości $n$.

String-matching w pamięci stałej dla specjalnych wzorów

Oznaczmy przez $MaxSuf(w)$ maksymalny leksykograficznie sufiks słowa $w$. Słowo $x$ nazwiemy specjalnym gdy $MaxSuf(x)=x$.

Przykład

'bajtocja' nie jest słowem specjalnym, ale rotacja tego słowa 'tocjabaj' jest.

Dlaczego słowa o tej własności są interesujące ? Większość szybkich algorytmów szukania podsłów korzysta z okresów $p$ prefiksów słowa. Liczenie tych okresów w ogólnym przypadku jest wąskim gardłem w projekcie algorytmu. Natomiast dla słow specjalnych liczenie okresów jest trywialne.

Jeśli $x$ jest specjalny to okres każdego prefiksu słowa $x$ można policzyć następującym naiwnym algorytmem;

Algorytm Funkcja Naiwne-Liczenie-Okresu (j)

---

$period:=1$;
for $i:=2$ to $j$ do
   if $x[i]\ne x[i-period]$ then $period:=i$;
return $period$;

Przykład

Funkcja Naiwne-Liczenie-Okresu daje zły wynik dla tekstów które nie są specjalne, na przykład załóżmy że $x=(aba{)}^{6}a=abaabaabaabaabaabaa$.} Wtedy kolejne wartości okresów dla pozycji $j=1,2,..$

są:

a	b	a	a	b	a	a	b	a	a	b	a	a	b	a	a	b	a	a
1	2	2	4	5	5	7	8	8	10	11	11	13	14	14	16	17	17	19

Zatem Naiwne-Liczenie-Okresu$(19)=19$, dla $x=(aba{)}^{6}a$, wynik całkowicie niepoprawny. Poprawność algorytmu jest wyjaśniona na rysunku. Korzystamy z prostej własności, że prefiks specjalnego słowa jest też specjalny.

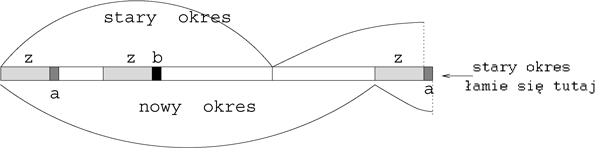
Rysunek 1: Załóżmy, że w algorytmie Naiwne-Liczenie-Okresu $x[i-period(i-1)]\ne x[i]$. Niech $a=x[i]$, $b=x[i-period]$. Ponieważ $uz$ jest prefiksem słowa specjalnego $x$ zatem $a<b$. Gdyby $period(i)<i$ to wtedy, ze względu na dwie okresowości, $zb$ jest właściwym podsłowem słowa $x[1..i-1]$ oraz $zb>x$. Zaprzecza to założeniu, że $x$ jest specjalne. Zatem $period(i)=i$.

Opiszemy teraz program szukania wzorca $x$ w slowie $y$i, zakładając że x jest sepcjalne. Program wczytuje dwa teksty, pierwszy z nich jest specjalne: $x$ pamiętamy w tablicy $x[0..m-1]$, $y$ w tablicy $y[0..n-1]$. Program wypisuje wszystkie wystapienia $x$ w $y$, tzn. wszystkie takie pozycje $i$, ze $y[i\dots i+m-1]=x$. Zapisujemy program w języku C++.

Algorytm Specjalny-String-Matching

---

void przesun() { if (j-1<2p) {i=i+p; j=0;} else {j=j-p; i=i+p;}}

}}

Program jest wstępem do programu szukajacego dowolne posłowo, niekoniecznie o wlasnosci bycia specjalnym. Postawowym niezmiennikiem w programie przed kazdym wykonaniem i po kazdym zakonczeniu pętli while' jest: (A)\ $x[0\dots j-1]=y[i\dots i+j-1]$, . (B)\ Program wypisal wszsytkie wczesniejsze wystapienia $i^{\prime }<i$, (C)\ $p$ jest okresem slowa $x[0\dots j-1]$

Algorytm działa w czasie liniowym, można to udowodnić obserwując zmiany wartości $2i+j$, zauważmy, że wartość ta nie zmniejsza się, a w wypadku pozytywnego testu $x[j)==y[i+j]$ zwiększa się co najmniej o 1. Jednocześnie $2i+j\le 3n$.

String-matching w pamięci stałej dla dowolnych wzorców

Algorytym Specjalny-String-Matching można łatwo zmodyfikować tak, aby znajdował on wystąpinia dowolnego słowa (niekoniecznie specjalnego) w czasie liniowym i stałej pamięci. Niech $x=uv$, gdzie $v$ jest leksykograficzne maksymalnym sufiksem $x$. Oznaczmy $r=|u|$. Technicznie informacja o rozkładzie $uv$ sprowadza się do pamiętania $r$.

Własność rozkładu. Niech $x=uv$ będzie rozkładem jak wyżej opisany. Wtedy Słowo $v$ występuje tylko raz w słowie $uv$. Jeśli $i^{\prime }<i$ są początkami wystąpień $v$, oraz $i-i^{\prime }<r$ to na pozycji $i-1$ nie kończy się wystąpienie $u$.

Z powyższego faktu wynika stosunkowo prosty algorytm szukania $x$ w czasie loiniowym i pamięci stałej. Algorytm ten jest modyfikacja agorytmu Specjalny-String-Matching , w ktorym rolę $x$ pełni $v$.

Algorytm String-matching w pamięci stałej

---

Niech $v$ będzie leksykograficznie maksymalnym sufiksem $x$;

Liczymy algorytmem Specjalny-String-Matching kolejne wystąpienia $v$ w $y$;

Dla każdego wystąpienia $i$ niech $i^{\prime }$ będzie wystąpieniem poprzednim;

jeśli $i-i^{\prime }\ge |v|$ to sprawdź czy $u$ występuje na lewo od pozycji $i$;

(sprawdzanie to wykonujemy w sposób naiwny)

jeśli występuje to wypisz kolejne wystąpienie całego wzorca $x$.

Pozostawiamy bardziej precyzyjny zapis algorytmu jako ćwiczenie.

W ten sposób pokazaliśmy, że problem szukania słowa $x$ w słowie $y$ można rozwiązać w czasie liniowym i pamięci (dodatkowej) stałej, jeśli znamy początkową pozycję $r$ leksykograficznie maksymalnego sufiksu $v$ słowa $x$.

Liczenie maksymalnego sufiksu w pamięci stałej

W algorytmie szukanie wzorca w pamięci stałej potrzebna jest pozycja $r$ od której zaczyna się maksymalny sufiks. Pokażemy teraz jak ją znajdować w czasie liniowym i w pamięci stałej. Kluczem do tego jest liczenie czegoś więcej, dla każdego prefiksu liczymy maksymalny sufiks jak również dodatkowo jego okres. To własnie liczenie okresu daje efektywność, chociaż na końcu nam ten okres jest niepotrzebny. Przekształcimy najpierw algorytm Naiwne-Liczenie-Okresu na algorytm liczący długość najdłuższego specjalnego prefiksu włącznie z jego okresem.

{algorytm| funkcja Najdłuższy-Specjalny-Prefiks(x)|fun_najdl_spec_pref| $period:=1$;
for $i:=2$ to $|x|$ do
   if $x[i]<x[i-period]$ \textbf{then} $period:=i$
   'else if $x[i]>x[i-period]$ then
      return $(i-1,period)$;
return $(|x|,period)$; }}

Skorzystamy z algorytmu Najdłuższy-Specjalny-Prefiks. Funkcja Maksymalny-Sufiks liczy początkową pozycję i okres maksymalnego sufiksu.

Algorytm funkcja Maksymalny-Sufiks(x)

---

$j:=1$;
repeat
   $(i,period):=$ Najdłuższy-Specjalny-Prefiks$(x[j..n])$;
   if $i=n$ then return $(j,period)$
   else $j:=j+i-(imodperiod)$;
forever

Możemy przepisać algorytm Maksymalny-Sufiks tak aby nie wywoływał on funkcji Najdłuższy-Specjalny-Prefiks, wpisując tę funkcję do algorytmu. Arytmetyczna funkcja $mod$ może być usunięta i zastąpiona przez operacje dodawania i odejmowania bez zmiany asymptotycznej złożoności.

Algorytm Maksymalny-Sufiks wykonuje co najwyżej $2.|x|$ porównań symboli. Uzasadnienie pozostawiamy jako ćwiczenie.

Algorytm funkcja} Maksymalny-Sufiks(x)

---

$s:=1$; $i:=2$; $p:=1$;
while ($i\le n$) do
   $r:=(i-s)modp$;
   if ($x[i]=x[s+r])$ then $i:=i+1$
   else if ($x[i]<x[s+r])$ then begin       $i:=i+1$; $p:=i-s$;    else       $s:=i-r$; $i:=s+1$; $p:=1$;
return $s$;

Kodowanie prefiksowe: drzewa i kody Huffmana

Zbiór słów jest prefiksowy gdy żadne słowo nie jest prefiksem drugiego. Taki zbiór słów odpowiada drzewu, którego ścieżki etykietowane są symbolami, w przypadku binarnym możemy przyjąć, że krawędź w lewo jest etykietowana zerem, a w prawo jedynką. Przez kodowanie rozumiemy funkcję $h$ która każdemu symbolowi $s$ przyporządkowuje niepusty ciąg binarny $h(s)$, całe słowo $x$ zostanie zakodowane na słowo $h(x)$ (każda litera jest zakodowana niezależnie i kody są skonkatenowane. Kod jest prefiksowy gdy zbiór kodów symboli jest prefiksowy. Rozważamy następujący problem.

Optymalne kodowanie prefiksowe

Dla danego słowa $x$ znaleźć binarne kodowanie prefiksowe takie, że $h(x)$ ma minimalną długość.

Przykład

Niech $x=abracadabra$. Liczby wystąpień symboli w słowie $x$ są:

$w_a=5,w_b=2,w_c=1,w_d=1,w_r=2.$

Optymalnym kodowaniem jest $h(a)=0,h(b)=10,h(c)=1100,h(d)=1101,h(r)=111.$ $abracadabra$ zostaje zakodowane na $01011101100011010101110$, ciąg binarny długości $23$. Optymalne drzewo binarne odpowiadające optymalnemu kodowi prefiksowemu jest pokazane na rysunku.

Rysunek 2:Drzewo Huffmana kodujące optymalnie symbole $a,b,c,d,r$ z wagami odpowiednio $S=(5,2,1,1,2)$. Liczby w wewnętrznych węzłach są sumą wag w liściach odpowiadającego poddrzewa. Koszt całkowity kodowania jest ważoną sumą długości ścieżek do liści, jest równeż sumą wartości w węzłach wewnętrznych: $2+4+6+11=23.$

Długość tekstu $h(x)$ jest równa ważonej sumie długości ścieżek, ważoenj w tym sensie, że długość ścieżki do danego liścia jest przemnożona przez wagę tego liścia. W przykładzie jest to suma: $5*1+2*2+1*4+1*4+2*3=23$.

Niech $n$ będzie liczbą różnych symboli w $x$, $w[i]$ będzie liczbą wystąpień $i$-tego symbolu. Problem możemy rozwiązać stosując algorytm dla problemu Optymalne Sklejanie Par dla ciągu $w[1],w[2],\dots w[n])$. Musimy algorytm zmodyfikować tak, aby nie tylko sklejał pary ale również tworzył lokalnie drzewo. Inaczej mówiąc algorytm w momencie sklejania elementów $a$, $b$ w element $c$ tworzy równieź dowiązania, $a$ staje się lewym synem $c$, natomiast $b$ staje się prawym synem.

Algorytm Huffmana (nieformalny opis)

---

Konfiguracje pośrednie algorytmu to zbiory drzew,

początkowo każdy pojedyńczy element $i$ z wagą $w[i]$ jest pojedyńczym drzewem.

Korzeń każdego drzewa reprezentuje sklejenie jego wszystkich liści.

Za każdym razem sklejamy dwa korzenie drzew o minimalnej wadze.

Drzewo które algorytm generuje nazywamy drzewem Huffmana.

Pozostawiamy jako ćwiczenie przerobienie algorytmu Optymalne-Sklejanie-Par na algorytm liczenia kodów i drzew Huffmana.

Z analizy algorytmu Optymalne Sklejanie Par wynika, że problem optymalnych binarnych kodów prefiksowych można rozwiązać w czasie $O(n\log n)$, a jeśli wagi $w[i]$ są posortowane to w czasie liniowym.

Kodowanie Huffmana słowami $k$-arnymi.

Pozostawiamy jako ćwiczenie podobny problem, ale gdy kodujemy w alfabecie $k$-arnym, mamy teraz symbole $0,1,\dots ,k-1$. W algorytmie jednorazowo możemy sklejać więcej niż dwa elementy.

Kodowanie prefiskowe z symbolami kodowymi nierównej długości

Problem robi się skomplikowany,gdy długość symbolu 0 jest 1 a długość symbolu 1 jest $c$, gdzie $c$ jest pewną stała (jest to po angielsku problem tzw. lopsided trees). Inaczej mówiąc szukamy takiego optymalnego drzewa, że ważona suma ścieżek jest minimalna, ale długość krawędzi na lewo wynosi 1 a długość krawędzi na prawo wynosi $c$. Pozostawiamy jako ćwiczenie znalezienie efektywnego algorytmu dla małych $c$ ($c=2$ lub $c=3$). Dla dowolnego $c$ (będącego częścia wejścia) i dowolnych wag jest to zbyt trudne, nie znamy algorytmu wielomianowego. Dla ustalonego c istnieje algorytm wielomianowy którego stopień zależy od c. Natomiast pozostawiamy jako ćwiczenie przypadek gdy $c$ jest dowolne ale wszystkie wagi $w[i]$ są równe.

Kodowanie prefiskowe z kodami o ograniczonej długości

Innym ciekawym problemem jest też skonstruowanie optymalnego kodu prefiksowego, w którym wszystkie słowa kodowe są ograniczone przez pewną zadaną liczbę $L$. Inaczej mówiąc ograniczamy z góry wysokość drzewa Huffmana. Istnieją algorytmy wielomianowe dla tego problemu, stopień wielomianu niezależny od $L$.

Problem minimalnego pokrywającego słowa

Pokażemy jeszcze proste bezpośrednie zastosowanie tablicy prefikso-sufiksów. Słowem pokrywającym tekst x taki tekst y, którego wystąpienia w x pokrywają cały tekst x. Na przykład aba pokrywa ababaaba, natomiast nie pokrywa tekstu abaaababa. Niech $S[i]$ będzie rozmiarem minimalnego pokrywajćego słowa dla prefiksu $x[1..i]$. Algorytm wykorzystuje następujący fakt: \ $S[i]=i\text{<mrow data-mjx-texclass="ORD">lub</mrow>}S[i]=S[P[i]].$ \ Następujący algorytm liczy długość minimalnego słowa pokrywającego tekstu x. Liczymy wartości $S[i]$ najmniejszej długości minimalnego słowa pokrywającego $x[1\dots i]$ dla każdego $1\le i\le n$. W $i$-tej iteracji algorytm pamięta jaki jest ``znany zakres każdego minimalnego słowa pokrywającego.

\begin{figure}[htb] \begin{center} \mbox{ \ } \includegraphics[width=6.4cm]{teksty_fig1.eps} \caption{$i$-ta iteracja algorytmu, dla $i=15$, oraz słowa $x=abaabababaababa\dots$. Tuż przed rozpoczęciem tej iteracji mamy $P[i]=8$, $q=S[8]=3$, $Zakres[3]=13$. Po zakończeniu $i$-tej iteracji mamy $S[15]=3,Zakres[3]=15$, ponieważ $i-Zakres[3]\le q$. } \end{center} \end{figure} \vskip 0.1cm \noindent Algorytm Rozmiar-Minimalnego-Pokrycia; \vskip 0.2cm for $i:=2$ to $n$ do \\ \hspace*{1cm} $Zakres[i]=i,S[i]=i$.\vskip 0.2cm for $i:=2$ to $n$ do\\ \hspace*{1cm} if $P[i]>0$ oraz $i-Zakres[S[P[i]]\le S[P[i]]$ then\\ \hspace*{1.8cm} $S[i]$ := $S[P[i]]$; \ $Zakres[S[P[i]]$ := $i$; \vskip 0.2cm return $S[n]$;