TTS Moduł 12

Cyfrowe łącze optyczne jest najważniejszym, elementarnym modułem współczesnego systemu telekomunikacyjnego na świecie. Wniosło ono do starych systemów telekomunikacyjnych trzy bardzo ważne cechy: ogromną, niewyobrażalną do niedawna przepustowość, znacznie mniejszą wrażliwość na szumy i tym samym lepsza wierność transmisji, uniwersalność jaką daje cyfryzacja wszelkiego rodzaju informacji. Tak więc łączem cyfrowym możemy z powodzeniem transmitować rozmowę, piosenkę, obraz, film, a także program komputerowy, bilans płatniczy firmy, itp. Znamy już narzędzia, z których można zbudować łącze optyczne. Czas poznać ich działanie.

---

Wykład, którego studiowanie zaczynamy jest długi i wprowadza nas w złożony świat łączy optycznych. Mam nadzieję, że będzie zrozumiały. Spis treści zawiera szereg ważnych tematów, które mogą być prezentowane w rozmaitej kolejności. Wydaje się, że najlepiej zacząć referowanie tematu na łączach analogowych, a skończyć na multipleksacji. Rozmiar wykładu każe nam opisywać bardzo krótko kolejne tematy, które wartą są osobnych wykładów.

---

Sygnał elektryczny może mieć formę sygnału analogowego bądź sygnału cyfrowego. Typowe sygnały analogowe to głosu z mikrofonu, obrazu z kamery video. Sygnały transmisji danych między komputerami są sygnałami cyfrowymi. Sygnały cyfrowe przyjmują kilka z możliwych wartości, sygnały binarne - jedną z dwu wartości ”1” lub ”0”. Sygnał analogowy zamieniamy na cyfrowy przez: próbkowanie go w określonym rytmie, kwantyzację próbki, czyli przypisanie jej jednej z M wartości, na co potrzeba m bitów: Obie funkcje wykonuje przetwornik A/D. Wartość próbki zostaje zapisana binarnie przez m bitów a informacja o tej wartości zostaje podana cyfrowo. Analogową postać sygnału przywraca przetwornik D/A. Przebieg analogowy nie zostaje odtworzony wiernie, zmienia się zawartość wyższych harmonicznych.

---

Wszystkie sygnały można ostatecznie zapisać w formacie cyfrowym. Transmisja cyfrowa staje się uniwersalnym sposobem na przesyłanie: dźwięku, obrazu i danych cyfrowych. Popatrzmy jakie pasma transmisji są wymagane przy transmisji rozmaitych danych. Transmisja rozmowy telefonicznej: pasmo: 200...3400 Hz; częstotliwość próbkowania: 8 kHz; rozdzielczość kwantowania 8 bitów; szybkość transmisji 64 kb/s; dynamika powiększona przez stosowanie logarytmicznej PCM. Audio-CD., popularny odtwarzacz: pasmo: 20...20 000 Hz; częstotliwość próbkowania: 44,10 kHz; rozdzielczość kwantowania 16 bitów; szybkość transmisji 706 kb/s na kanał. Digital Audio Tape – DAT: pasmo: 20...20 000 Hz; częstotliwość próbkowania: 48 kHz. Systemy telewizji: NTSC/PAL: szybkość transmisji 3...5 Mb/s. System telewizji zgodny z CCIR 601: szybkość transmisji 5...10 Mb/s; cyfrowy strumień danych zawiera informacje kolejno o 3 kolorach: czerwonym, zielonym i niebieskim; 3 przetworniki A/D analizuję każdy z kolorów zapisując intensywność barwy za pomocą 8 bitów. High Definition Television Format – HDTV: szybkość transmisji bez kompresji: 60 Mb/s; szybkość transmisji z kompresją: 20-40 Mb/s. Wnioski: Porównanie pasma zajętego przez transmisję sygnału analogowego z pasmem zajętym przez sygnał cyfrowy odwzorowujący przebieg analogowy wskazuje na znaczne powiększenie warunków szerokopasmowości;

---

Sieci telekomunikacyjne tworzą rozległe, nieregularne struktury, wśród których można wyodrębnić charakterystyczne elementy: LAN - Local-Area-Network, łączy niewielkie liczby użytkowników, najmniejsze z sieci. MAN - Metropolitan-Area-Network, większe struktury sieci telekomunikacyjnej. WAN - Wide-Area-Network, największe struktury sieci, budowane w dużych rejonach geograficznych. Łącza optyczne są jednym z elementów sieci, która poza tym może wykorzystywać: radiolinie, sieci telekomunikacji komórkowej, sieci satelitarne, sieci telefonii tradycyjnej, sieci CATV, itp.

---

Mimo rozwoju techniki transmisji cyfrowej, transmisja sygnałów w postaci analogowej jest ciągle istotnym elementem wielu systemów telekomunikacyjnych i radiolokacyjnych. Prosty schemat takiego łącza pokazano na rysunku. Sygnał analogowy dostarczony do nadajnika kierowany jest przez wzmacniacz $W_N$ do lasera. Którego moc optyczna modulowana jest w takt tego sygnału. Po transmisji światłowodem sygnał dociera do fotodetektora i po wzmocnieniu wzmacniaczem $W_0$ pojawia się na wyjściu odbiornika. Sygnał wyjściowy powinien być możliwie wierną kopią wejściowego. Oczywiście struktura łącza analogowego może być nieco inna. Rozwiązania takie poznamy w dalszych segmentach wykładu.

---

Zasada działania łącza analogowego z modulacją bezpośrednią jeszcze raz pokazana została na rysunku. Proces modulacji oparty na zamianie modulacji prądu diody laserowej na generowaną przez nią moc optyczną odbywa się z pewną sprawnością. Decydującym parametrem jest nachylenie charakterystyki diody laserowej $S_L[W/A]$. Proces konwersji mocy optycznej na prąd wyjściowy dokonujący się w odbiorniku optycznym dokonuje się także ze sprawnością określoną czułością detektora $R_D[A/W]$. W oparciu o te wielkości można proces modulacji i demodulacji ocenić z energetycznego punktu widzenia.

---

Zdefiniowane wzmocnienie nie zależy od poziomu mocy wyjściowej lasera i średniego prądu fotodetektora. Gdyby każdy elektron wstrzyknięty do obszaru aktywnego lasera generował jeden foton, i foton ten po dojściu do fotodetektora generował jedną parę dziura elektron, to wzmocnienie byłoby równe 1. Jednakże z wielu powodów jest mniejsze od jedności. W typowych łączach analogowych z bezpośrednią modulacją mocy optycznej lasera półprzewodnikowego wzmocnienia $G$ są zwykle mniejsze od –20 dB. Transmisja sygnału łączem analogowym z bezpośrednią modulacją lasera połączona jest z istotnym zmniejszeniem mocy sygnału. W specjalnych typach laserów o dużym nachyleniu $S_L$ można uzyskać wzmocnienia większe od –10 dB.

---

Układ ideowy łącza pokazano na rysunku. Sygnał optyczny kierowany jest do modulatora elektrooptycznego typu Mach-Zehnder’a. Charakterystyka tego modulatora ma kształt sinusoidalny, natomiast praca łącza analogowego wymaga liniowej charakterystyki modulacji. Dlatego przyjmuje się punkt polaryzacji modulatora w punkcie przegięcia charakterystyki – co pokazano na rysunku. Nachylenie charakterystyki w tym punkcie oznaczono przez $S_{MZ}[1/V]$. Odbiornik sygnałów optycznych jest identyczny, jak poprzednio. Parametrem określającym sprawność procesu zamiany sygnału optycznego na elektryczny jest czułość fotodetektora diodowego $R_D[A/W]$.

---

Maksymalna transmisja mocy optycznej modulatora M-Z $T_{MAX}<1$, gdyż modulator ma własne straty wynikłe ze stratności światłowodów planarnych. Głębokość modulacji mocy optycznej zależy od $(V_{RF}/V_x{)}^2$. Ta sama amplituda $V_{RF}$ może modulować małe, bądź duże moce optyczne $P_0$. A więc wzmocnienie łącza optycznego jest proporcjonalne do mocy wyjściowej $P_0$ lasera nadajnika. Największe wartości wzmocnień uzyskuje się dla łącza z modulacją zewnętrzną wykorzystującego lasery na ciele stałym Nd:YAG, o mocy optycznej kilku watów. Przy użyciu dużych mocy optycznych możliwym jest uzyskanie całkowitego wzmocnienia większego od 1.

---

Najpopularniejszym typem łącza optycznego jest łącze cyfrowe. Celem transmisji jest przesłanie - możliwie bezbłędnie - od nadajnika do odbiornika ciągu liczb. Najprostsze rozwiązanie łącza cyfrowego wykorzystuje technikę IM-DD (ang. Intensity Modulation – Direct Detection). Tak jak pokazano to na rysunku, łącze optyczne składa się z nadajnika, światłowodu i odbiornika. Przygotowany odpowiednio przez układy multipleksacji i kodowania sygnał trafia do nadajnika optycznego. Sygnał optyczny generowany przez nadajnik jest następnie transmitowany światłowodem kwarcowym do odbiornika. Sygnał optyczny, osłabiony tłumieniem światłowodu, z impulsami zniekształconymi efektami dyspersji, dopływa do odbiornika. W odbiorniku odbywa się detekcja bezpośrednia (Direct Detection), na diodzie PIN. Specjalne układy regenaracyjne przywracają kształt impulsom. Nastepnie odpowiednie uklady elektroniczne rozprowadzają sygnał do innych elementów sieci telekomunikacyjnej.

---

Na rysunku pokazano układ ideowy cyfrowego łącza światłowodowego z bezpośrednią, prądową modulacją mocy optycznej generowanej przez laser wraz z ilustracją procesów modulacji i detekcji. Wynikiem modulacji impulsy mocy optycznej, czyli grupy, paczki fotonów, które rozpoczynają podróż swiatłowodem. Przy modulacji impulsami odpowiadajacymi prędkości transmisji 10 Gb/s czas przepływu takiego impulsu wynosi niecałe 100 ps, a „paczka” fotonów zajmuje długość około 3 cm. Oczywiście gęstość fotonów nie jest jednakowa na całej długości „paczki” i nie jest czystym prostokatem, a raczej impulsem o kształcie zblżonym do krzywej Gaussa.

---

Dwustanowa modulacja amplitudy (modulacja mocy optycznej) typu „on-off keying” OOK jest także możliwa gdy zastosujemy modulator zenetrzny Mach-Zehndera. Aby wykorzystać w pełni możliwości modulatora powinniśmy modulować jego transmisję od stany maksymalnej transmisji do minimalnej. Niestety nie jest to transmisja równa zeru, w dobrych modulatorach moc minimalna spada do 1/40 mocy maksymalnej.

---

Moc nadajnika, czułość odbiornika i tłumienie światłowodu decydują o długości łącza. Jeśli jednak zwiększamy długość światłowodu moc docierająca do odbiornika może być zbyt mała, a stopa błędu zbyt duża. Aby zwiększyć długość łącza stosuje się wtedy wzmacniacze optyczne i układy regeneracyjne. Struktura łącza optycznego z łańcuchem wzmacniaczy i regeneratorów pokazana jest na rysunku. Układy regeneracyjne impulsów typu 3R (ang. repeater, regenerator: retiming, reshaping, regenerating) zawierają odbiornik optyczny, układy elektroniki i nadajnik optyczny. Odległości miedzy poszczególnymi elementami łącza są różne, zależą od pojemności łącza, mocy lasera, itp. Ogólnie można powiedzieć, że: wzmacniacze optyczne EDFA rozmieszczane są co 30…120 km, odległość między regeneratorami jest w granicach 50…600 km, odległość między terminalami do 600 km nie wymaga użycia regeneratora. Systemy długodystansowe do 10.000 km wymagają użycia wielu regeneratorów. Projektując takie systemy należy uwzględnić szereg innych warunków.

---

W systemach długodystansowych wykorzystywane są kable z wieloma jednomodowymi światłowodami. Łącza takie są zwykle dwulierunkowe. Na rysunkach pokazano jak wygląda struktura układów stacji wzmacniaczy i regeneratorów dla dwukierukowego łącza z dwiema parami światłowodów jednomodowych. Systemy z regeneratorami impulsów mają istotne wady: Nie mogą być stosowane w systemach z multipleksacja WDM, ponieważ laser nadajnika pracuje na jednej częstotliwości. Regeneratory są z natury rzeczy jednokierunkowe. Układy elektroniczne regeneratorów ograniczają szybkość transmisji.

---

Podstawowe kryterium pozwalające obliczyć zasięg łącza światłowodowego: moc odbierana musi być większa od mocy $P_R$ określającej czułość odbiornika, zwykle z marginesem $P_m=6dB$. Aby ocenić zasięg łącza przeprowadzimy analizę budżetu mocy. Oznaczymy dla potrzeb analizy następujące wielkości: Moc nadajnika laserowego $P_S[dBm]$, Stała tłumienia światłowodu $\alpha [dB/km]$, Dla długości $L[km]$ daje to tłumienie toru $\alpha L[dB]$, Straty wywołane połączeniami i sprzężeniami $P_C[bB]$, Czułość odbiornika $P_R$ z marginesem $P_m$. Dochodzimy do prostej zależności, opartej na budżecie mocy.

---

W transmisji cyfrowej dla „1” startuje z lasera grupa fotonów, dla „0” panuje cisza. Grupa fotonów maleje i kurczy się w miarę transmisji wzdłuż światłowodu, do odbiornika powinno ich dotrzeć co najmniej tyle, aby ten bezbłędnie (błąd mniejszy od $10^{-9}$) wykrył i zidentyfikował impuls. Z rozważań, które nie zostaną przedstawione, wynika, że w idealnym przypadku 10 fotonów wystarcza do identyfikacji jedynki. W rzeczywistości potrzeba na to średnio $n_0$ fotonów/bit. Można teraz obliczyć wartość mocy $P_R$ odpowiadającej czułości odbiornika i zauważyć, że wzrost prędkości transmisji to wzrost ilości impulsów w sekundzie, a jednocześnie coraz mniej fotonów w impulsie.

---

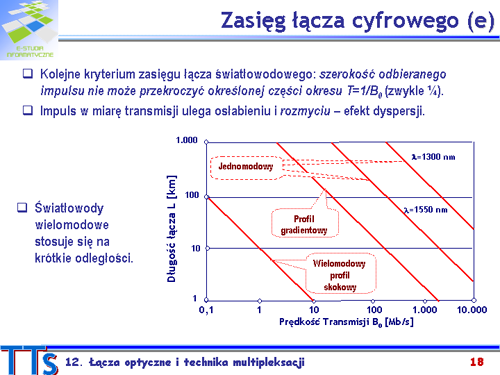
Kolejne kryterium pozwalające obliczyć zasięg łącza światłowodowego: szerokość odbieranego impulsu nie może przekroczyć określonej części okresu $T=1/B_0$ (wartość 1/4 przyjęto arbitralnie, do porównań). Sygnały monoczęstotliwościowe nie podlegają dyspersji, sygnały zajmujące pewne pasmo są przez efekt dyspersji modyfikowane. Impuls światła wzbudzony w światłowodzie ma kształt krzywej Gaussa. W miarę propagacji na długości L impuls ulega rozmyciu zachowując „Gaussowski” kształt. W światłowodzie wielomodowym decyduje dyspersja modalna. W światłowodzie wielomodowym pobudzane jest wiele modów, z których każdy wędruje samodzielnie z różną prędkością. Impuls wejściowy ulega „rozmyciu”. W światłowodzie jednomodowym prędkość grupowa zależy od długości fali, mamy do czynienia z dyspersją chromatyczną. Można wyróżnić dwa składniki dyspersji chromatycznej: dyspersję materiałową, związaną z zależnością $n(\lambda )$, opisana parametrem $D_{\lambda }$ i dyspersję falowodową, związana z zależnością $v_{grupowa}(\lambda )$, opisana parametrem $D_w$.

---

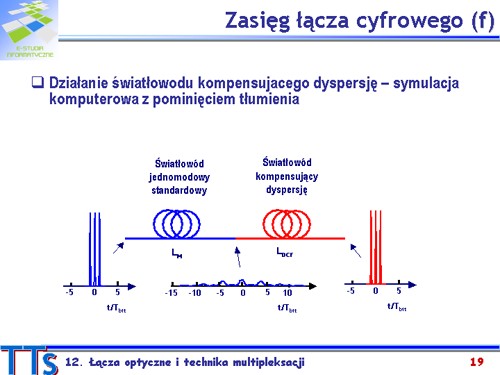
Światłowód jednomodowy spisuje się doskonale dla niewielkich prędkości transmisji ze względu na najmniejsze tłumienie. Niestety przy większych prędkościach transmisji daje o sobie znać dyspersja. Powstaje pytanie jak sobie z tym problemem poradzić? Opracowano technologię światłowodów o ujemnym współczynniku dyspersji. Światłowody takie mogą być odcinkami wprowadzane do toru transmisyjnego aby kompensować efekty dyspersji przy transmisji światłowodem standardowym. Działanie takiego odcinka pokazano na rysunku. Obliczenia kształtów impulsów przeprowadzono dla łącza z prędkością transmisji 40 Gb/s i długości impulsów 4,3 ps. Pierwszy odcinek to światłowód jednomodowy o współczynniku dyspersji 16ps/km.nm i długości $L_M=20km$. Drugi odcinek, to światłowód kompensujący dyspersję DCF (ang. Dispersion Compensating Fiber), o współczynniku dyspersji –90 ps/km.nm i długości $L_{DCF}=20*16/90km$. Efekty tłumienia pominięto.

---