CWGI Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 48: | Linia 48: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd5.png]] | ||
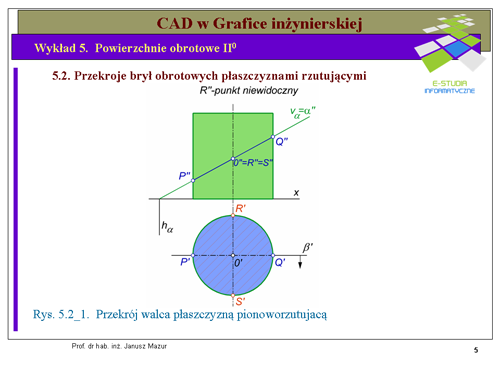
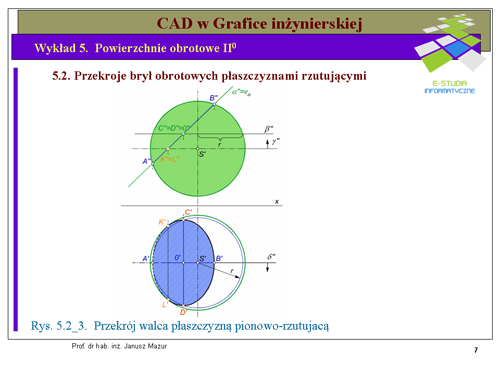
|valign="top"|Przekrojami brył obrotowych są krzywe stopnia II, takie jak elipsa, okrąg, parabola lub hiperbola. Najczęściej mamy do czynienia z przekrojami w postaci okręgu lub elipsy. Zwykle rzutem równoległym okręgu jest elipsa. Zatem skupimy się na tej krzywej, wyznaczając przekroje podstawowych brył obrotowych II stopnia, z jakimi mamy do czynienia w technice. Okrąg będziemy definiowali podając dwie średnice wzajemnie prostopadłe. Taka definicja pozwala ustalić środek okręgu oraz jego promień, jest ona wygodna, gdy będziemy definiować elipsę. | |valign="top"|Przekrojami brył obrotowych są krzywe stopnia II, takie jak elipsa, okrąg, parabola lub hiperbola. Najczęściej mamy do czynienia z przekrojami w postaci okręgu lub elipsy. Zwykle rzutem równoległym okręgu jest elipsa. Zatem skupimy się na tej krzywej, wyznaczając przekroje podstawowych brył obrotowych II stopnia, z jakimi mamy do czynienia w technice. Okrąg będziemy definiowali podając dwie średnice wzajemnie prostopadłe. Taka definicja pozwala ustalić środek okręgu oraz jego promień, jest ona wygodna, gdy będziemy definiować elipsę. | ||
| Linia 91: | Linia 91: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:CWGI_M5_Slajd9.png]] | ||
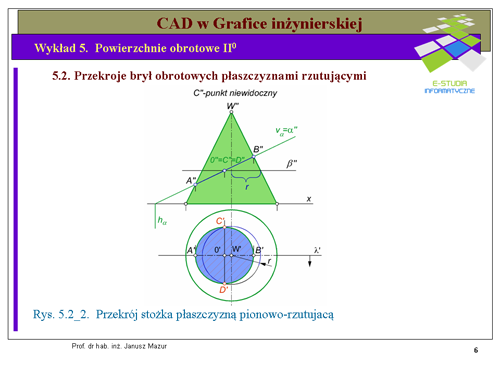
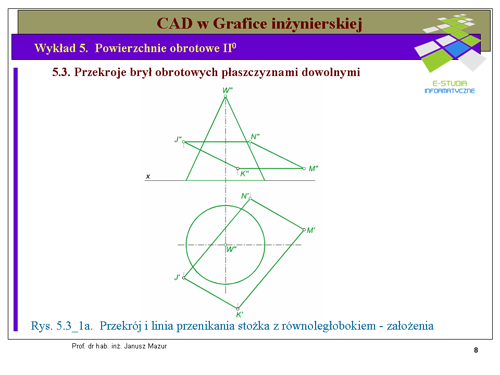
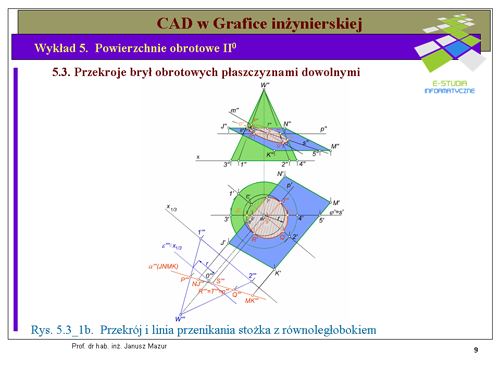
|valign="top"|Rozwiązanie zadania rozpoczynamy od zmiany układu odniesienia za pomocą transformacji tak, aby płaszczyzna krojąca była prostopadłą do rzutni (rys.5.3_1b). Ponieważ boki <math>JN</math> i <math>KM</math> równoległoboku są równoległe do rzutni poziomej (są prostymi poziomymi) oś transformacji <math>x_{1/3}</math> obieramy prostopadle do rzutów poziomych <math>J'N'</math> oraz <math>K'M'</math> boków równoległoboku. Po dokonaniu transformacji otrzymamy trzeci rzut stożka oraz trzeci rzut płaszczyzny równoległoboku <math>\alpha'''(JNMK)</math>. Przekrojem stożka, w tym przypadku jest elipsa (płaszczyzna <math>\alpha\,</math> nie kroi podstawy). W trzecim rzucie wyznaczymy bez trudu dwie osie prostopadłe elipsy <math>P'''Q'''</math> oraz <math>R'''T'''</math>, które jednoznacznie opisują jej zarys. Wracając do układu rzutów poziomego i pionowego, zgodnie z zasadami transformacji, otrzymamy rzuty poziome i pionowe tych osi, które będą tworzyły średnice sprzężone elips odpowiednio dla rzutów poziomego i pionowego. Średnice sprzężone elips również jednoznacznie określają zarys elipsy. Kolejnym zagadnieniem do rozwiązania jest ustalenie punktów styczności elipsy w rzucie pionowym z tworzącymi konturowymi stożka, zwanymi '''punktami zmiany widoczności'''. W tym celu ustalamy granice zmiany widoczności dla rzutu pionowego stożka. Jest to płaszczyzna przechodząca przez wierzchołek, prostopadła do rzutni poziomej i równoległa do rzutni pionowej, której rzut poziomy opiszemy literą <math>\phi'</math>. Prowadząc przez tą płaszczyznę prostą <math>s\,</math> leżącą w płaszczyźnie równoległoboku, możemy stwierdzić, iż będzie ona przechodziła również przez punkty zmiany widoczności, leżące na tworzących skrajnych w rzucie poziomym. Rzut pionowy prostej <math>s''</math> znajdziemy na rzucie pionowym równoległoboku <math>J''N''M''K''</math> wyznaczając kolejno rzuty punktów <math>5''</math> i <math>6''</math> należących do niej. Rzut pionowy prostej <math>s''</math> na tworzących skrajnych stożka w rzucie pionowym wyznaczy nam punkty zmiany widoczności <math>D''</math> i <math>C''</math>. Część elipsy przechodzącej przez punkty <math>R''D''C''</math> jest widoczna pozostała cześć elipsy jest niewidoczna. | |valign="top"|Rozwiązanie zadania rozpoczynamy od zmiany układu odniesienia za pomocą transformacji tak, aby płaszczyzna krojąca była prostopadłą do rzutni (rys.5.3_1b). Ponieważ boki <math>JN</math> i <math>KM</math> równoległoboku są równoległe do rzutni poziomej (są prostymi poziomymi) oś transformacji <math>x_{1/3}</math> obieramy prostopadle do rzutów poziomych <math>J'N'</math> oraz <math>K'M'</math> boków równoległoboku. Po dokonaniu transformacji otrzymamy trzeci rzut stożka oraz trzeci rzut płaszczyzny równoległoboku <math>\alpha'''(JNMK)</math>. Przekrojem stożka, w tym przypadku jest elipsa (płaszczyzna <math>\alpha\,</math> nie kroi podstawy). W trzecim rzucie wyznaczymy bez trudu dwie osie prostopadłe elipsy <math>P'''Q'''</math> oraz <math>R'''T'''</math>, które jednoznacznie opisują jej zarys. Wracając do układu rzutów poziomego i pionowego, zgodnie z zasadami transformacji, otrzymamy rzuty poziome i pionowe tych osi, które będą tworzyły średnice sprzężone elips odpowiednio dla rzutów poziomego i pionowego. Średnice sprzężone elips również jednoznacznie określają zarys elipsy. Kolejnym zagadnieniem do rozwiązania jest ustalenie punktów styczności elipsy w rzucie pionowym z tworzącymi konturowymi stożka, zwanymi '''punktami zmiany widoczności'''. W tym celu ustalamy granice zmiany widoczności dla rzutu pionowego stożka. Jest to płaszczyzna przechodząca przez wierzchołek, prostopadła do rzutni poziomej i równoległa do rzutni pionowej, której rzut poziomy opiszemy literą <math>\phi'</math>. Prowadząc przez tą płaszczyznę prostą <math>s\,</math> leżącą w płaszczyźnie równoległoboku, możemy stwierdzić, iż będzie ona przechodziła również przez punkty zmiany widoczności, leżące na tworzących skrajnych w rzucie poziomym. Rzut pionowy prostej <math>s''</math> znajdziemy na rzucie pionowym równoległoboku <math>J''N''M''K''</math> wyznaczając kolejno rzuty punktów <math>5''</math> i <math>6''</math> należących do niej. Rzut pionowy prostej <math>s''</math> na tworzących skrajnych stożka w rzucie pionowym wyznaczy nam punkty zmiany widoczności <math>D''</math> i <math>C''</math>. Część elipsy przechodzącej przez punkty <math>R''D''C''</math> jest widoczna pozostała cześć elipsy jest niewidoczna. | ||
Wersja z 09:35, 10 sie 2006

|
Powierzchnie obrotowe |