Inżynieria oprogramowania: Różnice pomiędzy wersjami

Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
← poprzednia edycjanastępna edycja →
WizualnieWikikod
Enawrocka (dyskusja | edycje)
502 edycje
Nie podano opisu zmian
Enawrocka (dyskusja | edycje)
502 edycje
Nie podano opisu zmian
Linia 1: Linia 1:
==Zadania – Metody formalne, sieci Petriego==
==Ćwiczenia – Metody formalne, sieci Petriego==


[[io-07-lab-wiki|<< Powrót do strony zadań]]
===Informacje wstępne===


===Odpowiedzi===
Przedstawione zadania dotyczyć będą zagadnienia budowy i analizy sieci Petriego.
 
Aby ułatwić tworzenie diagramów, zaleca się skorzystanie z darmowego
'''Zadanie 1:'''
symulatora sieci [http://pipe2.sourceforge.net/ PIPE2].
*<strike>T0, T1, T3, T4, T1</strike>
----
*T0, T1, T3, T2, T4, T1  
===Zadanie 1. Wyznaczanie możliwych sekwencji odpaleń===
*<strike>T0, T1, T2, T1, T3</strike>
Oznacz, które z poniższych sekwencji odpaleń przejść są możliwe dla sieci Petriego zaprezentowanej na rysunku 1.
*T0, T1, T3, T4, T1
*T0, T1, T3, T2, T4, T1
*T0, T1, T2, T1, T3
*T0, T1, T2, T3, T4, T1
*T0, T1, T2, T3, T4, T1


<flashwrap>file=io-07-lab01.swf|width=360|height=350</flashwrap>
[[Image:io-07-lab-rys1.png|sieć Petriego do zadania 1]]
 
T0, T1, T3, T2, T4, T1


<flashwrap>file=io-07-lab02.swf|width=360|height=350</flashwrap>
Rys. 1. Sieć Petriego do zadania 1


T0, T1, T2, T3, T4, T1


'''Zadanie 2:'''
[[io-07-lab-odp01-wiki|Odpowiedzi do zadania 1]]
*<strike>T1, T3, T5, T0, T3</strike>
----
===Zadanie 2. Wyznaczanie możliwych sekwencji odpaleń===
Oznacz, które z poniższych sekwencji odpaleń przejść są możliwe dla sieci Petriego zaprezentowanej na rysunku 2.
*T1, T3, T5, T0, T3
*T1, T3, T5, T2, T0, T3
*T1, T3, T5, T2, T0, T3
*<strike>T0, T3, T5, T1, T2</strike>
*T0, T3, T5, T1, T2
*T0, T2, T3, T5, T4
*T0, T2, T3, T5, T4
*T2, T0, T3, T5, T1, T4
*T2, T0, T3, T5, T1, T4
*<strike>T2, T0, T3, T4, T1</strike>
*T2, T0, T3, T4, T1
 
[[Image:io-07-lab-rys2.png|Sieć Petriego do zadania 2]]
 
Rys. 2. Sieć Petriego do zadania 2


<flashwrap>file=io-07-lab03.swf|width=380|height=370</flashwrap>


T1, T3, T5, T2, T0, T3
[[io-07-lab-odp02-wiki|Odpowiedzi do zadania 2]]
----
===Zadanie 3.Zamiana sieci na postać symboliczną===
Możliwy jest przejście z zapisu graficznego na postać symboliczną. W tym celu stosuje się oznaczenia:
*Jeśli przejścia występują sekwencyjnie wyszczególniamy je po kolei np. T1 T2,
*Jeśli przejścia mogą odpalić się równolegle oznaczamy je jako T1 || T2
*Jeśli pewna sekwencja przejść może odpalać się w pętli (T1 T2)*
Dla przykładowej sieci przedstawionej na rysunku 3, zapis ma postać
*( T0 ( T1 || T4 T5 ( T6 T7 T4 T5 )* T2 )*


<flashwrap>file=io-07-lab04.swf|width=380|height=370</flashwrap>
[[Image:io-07-lab-rys3.png|Sieć Petriego do przykładu ze zamianą na notację symboliczną]]


T0, T2, T3, T5, T4
Rys. 3. Sieć Petriego do przykładu ze zamianą na notację symboliczną


<flashwrap>file=io-07-lab05.swf|width=380|height=370</flashwrap>


T2, T0, T3, T5, T1, T4
Stwórz zapis w notacji symbolicznej dla sieci przedstawionej na rysunku 4.


'''Zadanie 3:'''
[[Image:io-07-lab-rys4.png|Sieć Petriego do zadania 3]]
*( T0 T1 T2 T6 ( T4 T6 )* T3 T5 )*


'''Zadanie 4:'''
Rys. 4. Sieć Petriego do zadania 3


[[Media:io-07-lab04.xml|Plik w formacie PIPE2]]


Rozwiązanie przedstawiono na rysunku 5.
[[io-07-lab-odp03-wiki|Odpowiedzi do zadania 3]]
----
===Zadanie 4. Projektowanie sieci===
Należy zaprojektować sieć Petriego dla problemu czytelników i pisarzy, przy założeniach:
*jest jeden pisarz i trzech czytelników,
*jeśli pisarz pisze, żaden czytelnik nie może czytać,
*jeśli jeden czytelnik czyta, pozostali też mogą rozpocząć czytanie,
*jeśli któryś czytelnik czyta, pisarz nie może rozpocząć pisania


[[Image:io-07-lab-rys5.png|Sieć Petriego do zadania 4]]


Rys. 5. Sieć Petriego do zadania 4
[[io-07-lab-odp04-wiki|Odpowiedzi do zadania 4]]
----


<flashwrap>file=io-07-lab05.swf|width=460|height=320</flashwrap>
==Pytania do dyskusji==
#Czy sieci sieci Petriego nadają się do modelowania każdego oprogramowania?
#Jakie są ograniczenia stosowania metod formalnych w przemyśle?

Wersja z 13:51, 9 sie 2006

Ćwiczenia – Metody formalne, sieci Petriego

Informacje wstępne

Przedstawione zadania dotyczyć będą zagadnienia budowy i analizy sieci Petriego. Aby ułatwić tworzenie diagramów, zaleca się skorzystanie z darmowego symulatora sieci PIPE2.

Zadanie 1. Wyznaczanie możliwych sekwencji odpaleń

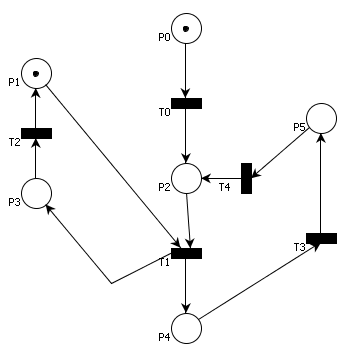
Oznacz, które z poniższych sekwencji odpaleń przejść są możliwe dla sieci Petriego zaprezentowanej na rysunku 1.

  • T0, T1, T3, T4, T1
  • T0, T1, T3, T2, T4, T1
  • T0, T1, T2, T1, T3
  • T0, T1, T2, T3, T4, T1

sieć Petriego do zadania 1

Rys. 1. Sieć Petriego do zadania 1


Odpowiedzi do zadania 1

Zadanie 2. Wyznaczanie możliwych sekwencji odpaleń

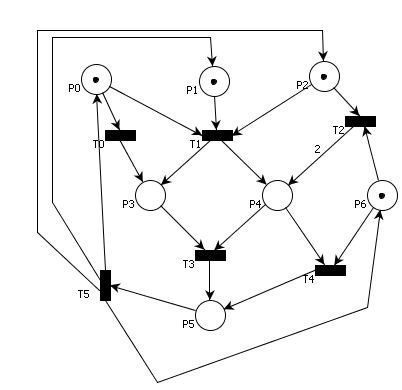
Oznacz, które z poniższych sekwencji odpaleń przejść są możliwe dla sieci Petriego zaprezentowanej na rysunku 2.

  • T1, T3, T5, T0, T3
  • T1, T3, T5, T2, T0, T3
  • T0, T3, T5, T1, T2
  • T0, T2, T3, T5, T4
  • T2, T0, T3, T5, T1, T4
  • T2, T0, T3, T4, T1

Sieć Petriego do zadania 2

Rys. 2. Sieć Petriego do zadania 2


Odpowiedzi do zadania 2

Zadanie 3.Zamiana sieci na postać symboliczną

Możliwy jest przejście z zapisu graficznego na postać symboliczną. W tym celu stosuje się oznaczenia:

  • Jeśli przejścia występują sekwencyjnie wyszczególniamy je po kolei np. T1 T2,
  • Jeśli przejścia mogą odpalić się równolegle oznaczamy je jako T1 || T2
  • Jeśli pewna sekwencja przejść może odpalać się w pętli (T1 T2)*

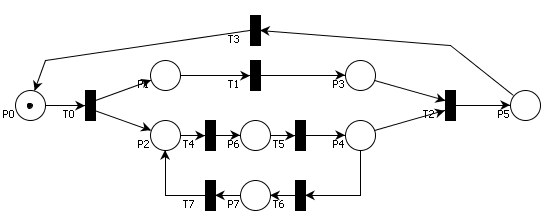
Dla przykładowej sieci przedstawionej na rysunku 3, zapis ma postać

  • ( T0 ( T1 || T4 T5 ( T6 T7 T4 T5 )* T2 )*

Sieć Petriego do przykładu ze zamianą na notację symboliczną

Rys. 3. Sieć Petriego do przykładu ze zamianą na notację symboliczną


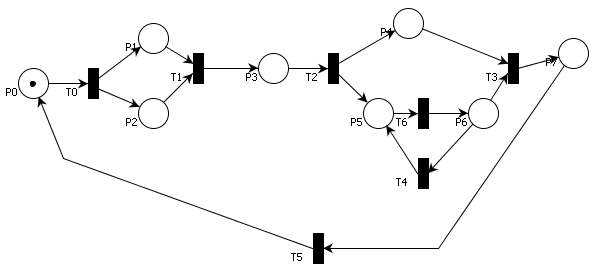
Stwórz zapis w notacji symbolicznej dla sieci przedstawionej na rysunku 4.

Sieć Petriego do zadania 3

Rys. 4. Sieć Petriego do zadania 3


Odpowiedzi do zadania 3

Zadanie 4. Projektowanie sieci

Należy zaprojektować sieć Petriego dla problemu czytelników i pisarzy, przy założeniach:

  • jest jeden pisarz i trzech czytelników,
  • jeśli pisarz pisze, żaden czytelnik nie może czytać,
  • jeśli jeden czytelnik czyta, pozostali też mogą rozpocząć czytanie,
  • jeśli któryś czytelnik czyta, pisarz nie może rozpocząć pisania


Odpowiedzi do zadania 4

Pytania do dyskusji

  1. Czy sieci sieci Petriego nadają się do modelowania każdego oprogramowania?
  2. Jakie są ograniczenia stosowania metod formalnych w przemyśle?
Źródło: „https://wazniak.mimuw.edu.pl/index.php?title=Inżynieria_oprogramowania&oldid=12183”