CWGIĆwiczenie 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 36: | Linia 36: | ||
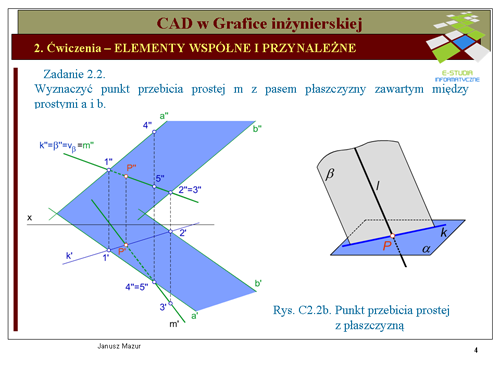
Do pełnego rozwiązania zadania niezbędne jest ustalenie widoczności prostej '''''m''''', przy założeniu, że pas między prostymi '''''a''''' i '''''b''''' jest nieprzezroczysty. W tym celu w miejscu przecięcia się rzutów prostej '''''m''''' z prostą należącą do płaszczyzny <math>\alpha\,</math> ( np. '''''a''''') obieramy punkty i analizujemy, które z nich mają większą głębokość (dla rzutów pionowych) względnie wysokość (dla rzutów poziomych). Np. analizując punkty: punkt <math>2''</math>, należący do prostej '''''m''''' oraz punkt <math>3''</math> należący do prostej '''''b''''', widzimy w rzucie poziomym, że punkt '''''3''''' ma większą głębokość, a więc prosta '''''m''''' w tym punkcie, w rzucie pionowym jest widoczna, prosta '''''b''''' jest niewidoczna, co oznaczamy linią kreskową aż do punktu przebicia <math>P''</math>. Analogiczne postępowanie przeprowadzamy dla punktów <math>4'</math> i <math>5'</math>, należących do prostych '''''a''''' i '''''m'''''. | Do pełnego rozwiązania zadania niezbędne jest ustalenie widoczności prostej '''''m''''', przy założeniu, że pas między prostymi '''''a''''' i '''''b''''' jest nieprzezroczysty. W tym celu w miejscu przecięcia się rzutów prostej '''''m''''' z prostą należącą do płaszczyzny <math>\alpha\,</math> ( np. '''''a''''') obieramy punkty i analizujemy, które z nich mają większą głębokość (dla rzutów pionowych) względnie wysokość (dla rzutów poziomych). Np. analizując punkty: punkt <math>2''</math>, należący do prostej '''''m''''' oraz punkt <math>3''</math> należący do prostej '''''b''''', widzimy w rzucie poziomym, że punkt '''''3''''' ma większą głębokość, a więc prosta '''''m''''' w tym punkcie, w rzucie pionowym jest widoczna, prosta '''''b''''' jest niewidoczna, co oznaczamy linią kreskową aż do punktu przebicia <math>P''</math>. Analogiczne postępowanie przeprowadzamy dla punktów <math>4'</math> i <math>5'</math>, należących do prostych '''''a''''' i '''''m'''''. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_CW2_Slajd5.png]][[Grafika:CWGI_CW2_Slajd6.png]] | |||
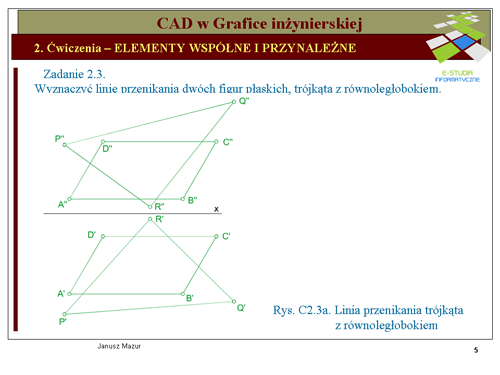
|valign="top"|''Zadanie 2.3.'' | |||
''Wyznaczyć linię przenikania dwóch figur płaskich, trójkąta '''PQR''' z równoległobokiem '''ABCD'''. Przyjmując, że płaszczyzny figur są nieprzezroczyste ustalić ich widoczność.'' | |||
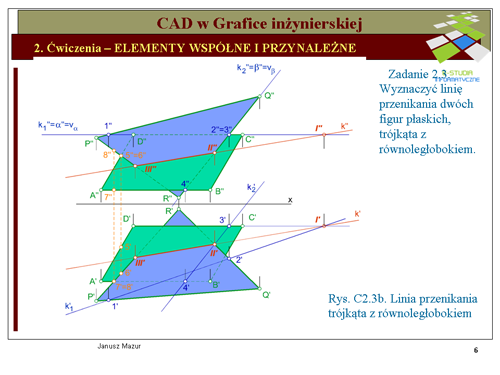
Linia przenikania figur płaskich to nic innego jak odcinek krawędzi przecięcia się płaszczyzn, zdefiniowanych przez te figury, wspólny dla obu płaszczyzn. Należy, zatem wyznaczyć wspólną krawędź przecięcia się płaszczyzn reprezentowanych przez trójkąt i równoległobok. Krawędź wyznaczymy metodą pośrednią, poszukując punktów przebicia bokiem jednej z figur płaszczyzny drugiej figury. Wyznaczenie dwóch punktów przebicia, czyli dwóch punktów wspólnych tych płaszczyzn określi nam krawędź przecięcia się płaszczyzn (dwa punkty, jednoznacznie, określają prostą). | |||
1). Wyznaczmy punkt przebicia boku '''''CD''''' równoległoboku z płaszczyzną trójkąta '''''PQR'''''. W tym celu poprowadzimy płaszczyznę pionowo - rzutującą <math>\alpha\,</math> przez bok '''''CD''''' równoległoboku. Płaszczyzna jest rzutująca, a więc krawędź przecięcia się tej płaszczyzny z płaszczyzną równoległoboku <math>k_1\,</math> będzie leżała w płaszczyźnie <math>\alpha\,</math>, ale również w płaszczyźnie trójkąta. Rzut pionowy tej krawędzi będzie pokrywał się z rzutem pionowym płaszczyzny <math>\alpha\,</math> oraz z rzutem pionowym boku <math>C''D''</math>. Przynależność krawędzi <math>k_1\,</math> do płaszczyzny trójkąta oznacza, że punkty <math>1''</math> i <math>2''</math> są rzutami punktów przecięcia się krawędzi z rzutami boków <math>P''Q''</math> oraz <math>R''Q''</math>. Rzuty poziome tych punktów znajdziemy na przecięciu się odnoszących prostopadłych do osi '''''x''''' z rzutami poziomymi boków trójkąta <math>P'Q'</math> oraz <math>R'Q'</math>. W ten sposób znajdujemy rzuty krawędzi <math>{k_1}''</math> oraz <math>{k_1}'</math>. W rzucie poziomym otrzymamy szukany punkt przebicia <math>{II}'</math> boku <math>C'D'</math> równoległoboku z płaszczyzną trójkąta. | |||
|} | |} | ||
<hr width="100%"></math> | <hr width="100%"></math> | ||
Wersja z 16:19, 7 sie 2006
</math>