CWGIĆwiczenie 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 25: | Linia 25: | ||
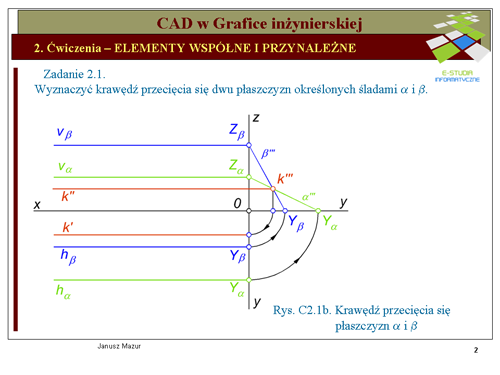
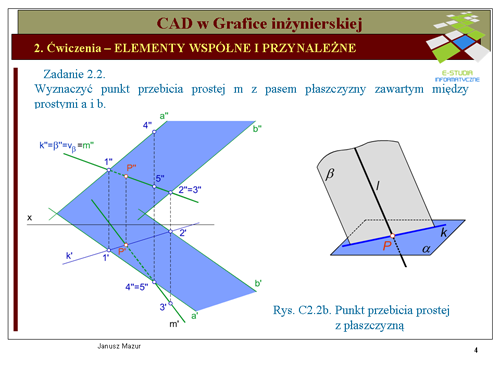
Rozwiązując zadanie musimy się zastanowić nad trybem postępowania. W tym przypadku powinniśmy postąpić w sposób następujący: | Rozwiązując zadanie musimy się zastanowić nad trybem postępowania. W tym przypadku powinniśmy postąpić w sposób następujący: | ||
#przez prostą '''''m''''' poprowadzić dowolną płaszczyznę <math>\beta\,</math>, najwygodniej rzutująca (pionowo-zutującą,) | |||
#wyznaczyć krawędź '''''k''''', przecięcia się płaszczyzny <math>\beta\,</math> z płaszczyzna <math>\alpha (a||b)</math>, | |||
#punkt, w którym krawędź '''''k''''' przetnie daną prostą '''''m''''' jest poszukiwanym punktem '''''P''''', przebicia prostej '''''m''''' z płaszczyzną <math>\alpha\,</math> | |||