CWGI Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 94: | Linia 94: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd8.png]] | ||
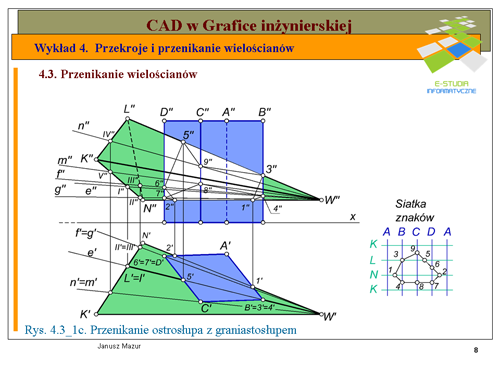
|valign="top"| | |valign="top"|W etapie II zajmiemy się punktami przecięcia krawędzi graniastosłupa ze ścianami ostrosłupa (patrz rys. 4.3_1c). | ||
Kolejne punkty przecięcia krawędzi graniastosłupa ze ścianami ostrosłupa to: punkty <math>6\,</math> i <math>7\,</math> przebicia krawędzi <math>D\,</math> ze ścianami odpowiednio <math>NLW</math> i <math>NKW</math> oraz punkty <math>8\,</math> i <math>9\,</math> przebicia krawędzi <math>C\,</math> ze ścianami <math>KLW</math> i <math>KNW</math>. Rzuty pionowe tych punktów wyznaczymy po ustaleniu rzutów pionowych poszczególnych tworzących przechodzących przez te punkty. | |||
Końcowym akcentem tego etapu jest wyznaczanie linii przenikania, a więc ustalenie, które punkty należy połączyć ze sobą tak, aby utworzyły zamkniętą linię przenikania. Powracamy zatem do '''siatki znaków''' Zasada łączenia ze sobą poszczególnych punktów polega na łączeniu ze sobą jedynie w obrębie jednego kwadratu. Powstała, zatem zamknięta linia przenikania. Może się zdarzyć, że otrzymamy dwie, pozornie otwarte linie przenikania, wtedy, gdy przecięcie wielościanu nastąpi wzdłuż krawędzi zaangażowanej w procesie konstrukcji linii przenikania. Pamiętając jednak, że powierzchnie boczne wielościanów są zamknięte oraz, że na końcu siatki powtarzamy pierwsza krawędź, zawsze otrzymamy linie zamkniętą. Tak otrzymane połączenia punktów linii przenikania nanosimy następnie, cienką linią, na rysunek konstrukcyjny. | |||
|} | |} | ||
| Linia 101: | Linia 106: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd9.png]] | ||
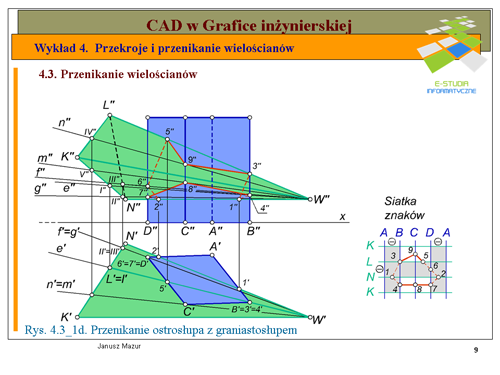
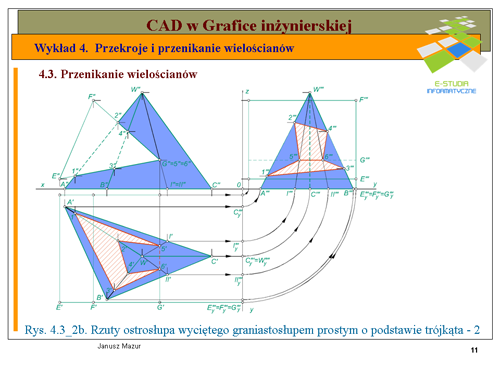
|valign="top"| | |valign="top"|Ostatni III etap związany jest z wyznaczaniem widoczności linii przenikania w rzucie pionowym(rys. 4.3_1d). Analizując rzut poziomy wielościanów ustalimy, które ze ścian są widoczne, a które są niewidoczne w rzucie pionowym. Analizę taką przeprowadzamy odrębnie dla każdego z wielościanów. W przypadku graniastosłupa niewidocznymi są ściany <math>AB</math> i <math>DA</math>, co zaznaczamy znakiem (-), a następnie całą ścianę na siatce znaków kreskujemy. Dla ostrosłupa niewidoczna jest ściana <math>LN</math>, którą również oznaczamy znakiem (-) i całą ścianę kreskujemy. Otrzymaliśmy, zatem pola kwadratów, w których znajdująca się linia przenikania jest niewidoczna oraz pola, w których jest ona widoczna. Tak otrzymaną, na siatce znaków, sytuację nanosimy na układ rzutów prostokątnych wielościanów. Ostatecznie przyjmując, że ściany wielościanów są nieprzezroczyste możemy uwypuklić wzajemne przenikanie się brył za pomocą cieniowania każdej z nich osobno. Uwzględniając widoczność poszczególnych odcinków linii przenikania możemy zacieniować ściany wielościanów w odrębny sposób dla każdego z nich. Zadanie powyższe zostało rozwiązane. | ||
|} | |} | ||
| Linia 108: | Linia 113: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:CWGI_M4_Slajd10.png]] | ||
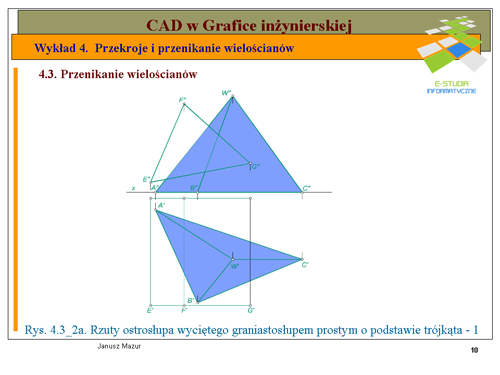
|valign="top"| | |valign="top"|Występujące w praktyce konstrukcyjnej częste przypadki „wycięcia” z brył przestrzennych określone otwory, przy pomocy specjalnych wykrojników. Wyznaczymy, zatem rzuty ostrosłupa z wyciętym otworem, przy pomocy wykrojnika w postaci prostego graniastosłupa trójkątnego. | ||
Niech będzie dany ostrosłup o podstawie trójkąta, którego poszczególne wierzchołki opisano literami <math>ABCW</math>. ''Należy wyznaczyć trzy rzuty ostrosłupa z wyciętym otworem, przy pomocy graniastosłupa trójkątnego '''EFG''' ''. | |||
Rozwiązanie zadania związane jest z wyznaczaniem linii przenikania między ostrosłupem i graniastosłupem. Założenia do zadania przedstawiono na rys. 4.3_2a. | |||
|} | |} | ||
Wersja z 13:04, 7 sie 2006

|
Wykład 4. Przekroje i przenikanie wielościanów |
|

|