CWGI Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 118: | Linia 118: | ||
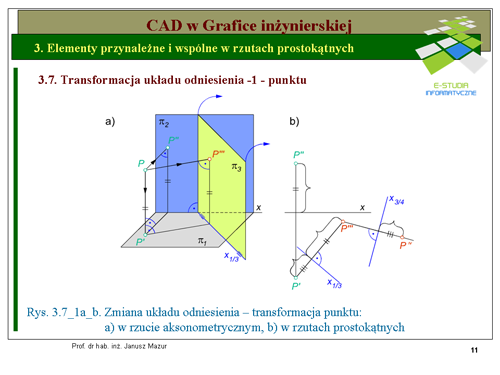
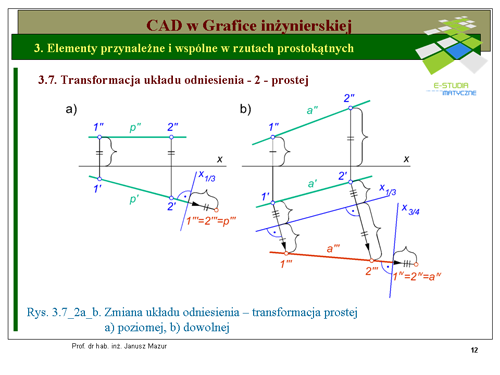
Sprowadzenie prostej w położeniu dowolnym do położenia rzutującego (do punktu) możliwe jest za pomocą podwójnej transformacji (3.7_2b). W pierwszej sprowadzamy prostą do położenia równoległego z trzecią rzutnią, a następnie za pomocą rzutni czwartej prostopadłej do trzeciego rzutu sprowadzamy ją do położenia rzutującego. W pierwszej transformacji przyjmujemy trzecią rzutnię równolegle do prostej oś transformacji <math>x_{1/3}</math> będzie równoległa do rzutu poziomego prostej <math>a'</math>). Druga transformacja o osi <math>x_{3/4}</math> będzie prostopadła do trzeciego rzutu. Odmierzając od osi <math>x_{3/4}</math> odległość rzutu poziomego a' od pierwszej osi transformacji otrzymamy czwarte rzuty punktów oraz czwarty rzut prostej <math>p^{IV}</math>, który również będzie punktem. | Sprowadzenie prostej w położeniu dowolnym do położenia rzutującego (do punktu) możliwe jest za pomocą podwójnej transformacji (3.7_2b). W pierwszej sprowadzamy prostą do położenia równoległego z trzecią rzutnią, a następnie za pomocą rzutni czwartej prostopadłej do trzeciego rzutu sprowadzamy ją do położenia rzutującego. W pierwszej transformacji przyjmujemy trzecią rzutnię równolegle do prostej oś transformacji <math>x_{1/3}</math> będzie równoległa do rzutu poziomego prostej <math>a'</math>). Druga transformacja o osi <math>x_{3/4}</math> będzie prostopadła do trzeciego rzutu. Odmierzając od osi <math>x_{3/4}</math> odległość rzutu poziomego a' od pierwszej osi transformacji otrzymamy czwarte rzuty punktów oraz czwarty rzut prostej <math>p^{IV}</math>, który również będzie punktem. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd13.png]] | |||
|valign="top"|Transformacja płaszczyzny ma na celu sprowadzenie jej do położenia rzutującego (do prostej). Szereg konstrukcji w rzutach prostokątnych rozwiązuje się w sposób nieskomplikowany, jeżeli mamy do czynienia z płaszczyzną w położeniu rzutującym. Zatem zmiana układu odniesienia w taki sposób, aby rozważana płaszczyzna była w położeniu rzutującym daje wymierne korzyści, albowiem wszystkie elementy płaskie znajdujące się w tej płaszczyźnie będą rzutowały się w trzecim rzucie na trzeci rzut płaszczyzny. | |||
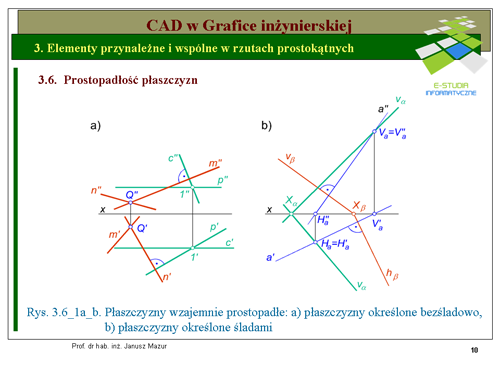
'''Aby sprowadzić płaszczyznę dowolną do położenia rzutującego należy oś transformacji wybrać prostopadle do śladu poziomego płaszczyzny, w przypadku transformacji na płaszczyznę prostopadłą do rzutni poziomej lub prostopadle do śladu pionowego płaszczyzny, jeżeli dokonujemy transformacji na płaszczyznę prostopadłą do rzutni pionowej.''' | |||
Mając do czynienia z płaszczyzną określoną bezśladowo osi transformacji przyjmujemy prostopadle do rzutu poziomego prostej poziomej, w pierwszym przypadku, lub do rzutu pionowego prostej czołowej w drugim przypadku. Zatem wstępną czynnością będzie ustalenie rzutów prostej poziomej (czołowej) leżącej w analizowanej płaszczyźnie. Na rys. 3.7_2a przedstawiono konstrukcję zmiany układu odniesienia za pomocą transformacji dla płaszczyzny określonej dwoma prostymi równoległymi oraz określonej śladami na rys. 3.7_2b | |||
W przypadku sprowadzania płaszczyzny określonej przez dwie proste równoległe do położenia rzutującego obieramy prostą poziomą leżącą w tej płaszczyźnie. Rzut pionowy prostej poziomej <math>p''\,</math> będzie równoległy do osi <math>x\,</math>. Na rzutach poziomych prostych <math>a'\ i\ b'</math> znajdziemy rzuty punktów <math>1'\ i\ 2'</math> należących do tych prostych i w konsekwencji wyznaczymy rzut poziomy prostej <math>p'\,</math>. Wyznaczając oś transformacji <math>x_{1/3}</math> , ustalimy trzecie rzuty punktów <math>1'''\ i\ 2'''</math> oraz <math>p'''\,</math>. Wystarczy, zatem obrać jeszcze jeden punkt (np.3) nie współliniowy z punktami <math>1\ i\ 2</math>, aby po przeprowadzeniu transformacji tego punktu wyznaczyć jego trzeci rzut, przy tej samej osi transformacji. Rzuty punktów <math>1'''\, 2'''</math> oraz <math>3'''\,</math> wyznaczają nam trzeci rzut płaszczyzny, który będzie prostą. Płaszczyzna <math>\alphaa||b</math> ma w układzie <math><\pi_1,\pi_3></math> położenie rzutujące. | |||
Przy sprowadzaniu płaszczyzny określonej śladami do położenia rzutującego postępujemy bardzo podobnie. W tym przypadku oś transformacji <math>x_{1/3}</math> będzie prostopadła do śladu poziomego płaszczyzny <math>\alpha</math> Ponieważ ślad poziomy płaszczyzny jest szczególnym położeniem prostej poziomej leżącej w płaszczyźnie, to punkt przecięcia się śladu poziomego z osią transformacji <math>x_{1/3}</math> - oznaczony <math>X\alpha''</math>'zwany węzłem płaszczyzny będzie punktem należącym do trzeciego rzutu płaszczyzny. Należy zatem obrać jeszcze jeden punkt nie należący do śladu poziomego (np. punkt 1), aby po dokonaniu transformacji tego punktu, przy tej samej osi <math>x_{1/3}</math> , ustalić jego trzeci rzut. Punkty <math>1'''\ i\ X+\alpha'''</math> wyznaczą nam trzeci rzut płaszczyzny <math>\alpha'''</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_M3_Slajd1.png]] | |||
|valign="top"|Ważnym zagadnieniem w grafice inżynierskiej jest wyznaczanie przekrojów brył płaszczyznami. Przedstawiona w poprzednich wykładach wiedza pozwoli nam zająć się tym zagadnieniem. Pierwszyą kwestia jest wyznaczanie przekrojów wielościanów płaszczyznami w położeniu szczególnym, a więc pionowo lub poziomo – rzutującym. | |||
Rozwiążmy zadanie na przykładzie dwóch wielościanów ostrosłupa prostego stojacego na rzutni poziomej i graniastosłupa pochyłego stojacego na rzutni poziomej. W pierwszym przypadku wyznaczymy rzuty przekroju ostrosłupa '''ABCW''' stojącego na rzutni poziomej płaszczyzną pionowo - rzutującą <math> \alpha</math> (rys. 3.8_1a). | |||
Zbudujmy w rzutach prostokątnych ostrosłup prosty o podstawie trójkąta stojący na rzutni poziomej oraz przyjmijmy płaszczyznę pionowo - rzutującą określoną śladami <math>v_alpha\ i\ h\alpha</math>. Ponieważ płaszczyzna <math>alpha</math> jest rzutująca to wszystkie elementy płaskie znajdujące się w płaszczyźnie, w rzucie pionowym będą znajdować się na rzucie pionowym płaszczyzny <math>\alpha</math>, czyli na śladzie pionowym płaszczyzny <math> v\alpha</math>. Tak więc przekrój w rzucie pionowym wyznaczymy znajdując punkty przecięcia się śladu <math>v\alpha</math> z rzutami pionowym krawędzi ostrosłupa <math>A''W''</math>, <math>B''W''</math> i<math> C''W''</math>. Przekrój w rzucie pionowym będzie wyznaczony przez rzuty punktów <math>1'',\ 2''\ i\ 3''</math>. Rzut poziomy przekroju wyznaczymy jako wielokąt, którego wierzchołkami są punktami przecięcia odnoszących z rzutami poziomymi krawędzi <math> A'W',\ B'W'\ i\ C'W'.</math> | |||
Drugi przykład dotyczy graniastosłupa. Należy wyznaczyć rzuty przekroju graniastosłupa pochyłego '''ABC''' o podstawie na rzutni poziomej płaszczyzną pionowo - rzutującą <math>\alpha</math>rys.3.8_1b). | |||
Przy rozwiązywaniu tego przykładu postępujemy analogicznie jak na rys. 3.8_1a. | |||
Po wyznaczeniu rzutów przekroju należy zwrócić uwagę na widoczność krawędzi. Zagadnienie to było już omawiane wcześniej przypomnijmy, zatem, iż analizę widoczności dla rzutu poziomego przeprowadzamy analizując rzut pionowy, badając wysokości punktów pozornie przecinających się boków w rzucie poziomym, z kierunku prostopadłego do rzutni pionowej. Widoczność w rzucie pionowy.przeprowadzamy analizując rzut poziomy (badając głębokość), z kierunku prostopadłego do rzutni pionowej. W przypadku przykładów omawianych powyżej w ostrosłupie wszystkie krawędzie są widoczne, zarówno w rzucie poziomym jak i pionowym. Dla graniastosłupa krawędzie w rzucie pionowym będą widoczne, natomiast krawędź <math>B'C'</math> oraz leżąca na tej ścianie krawędź przekroju <math>2'3'</math> będą niewidoczne ( patrz analiza wysokości punktów <math>4\ i\ 5</math>). | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 12:36, 7 sie 2006

|
Elementy równoległe i prostopadłe |