CWGI Moduł 1: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 74: | Linia 74: | ||
<math>k^{\infty ^\ | <math>k^{\infty ^\longrightarrow}</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd8.png]] | |||
|valign="top"|Zauważmy, że własności rzutu <math>G'\,</math> tworu <math>G\,</math> nie są identyczne jak własności samego tworu G. Wynika to między innymi z faktu, że twór może być bryłą przestrzenną, natomiast jego rzut równoległy zawsze jest figurą płaską. Jednak niektóre własności tworów nie ulegają zmianie po dokonaniu operacji rzutowania równoległego. Własności te nazwane zostały '''niezmiennikami rzutu równoległego'''. Niezmienniki rzutowania równoległego można opisać w sposób następujący: | |||
'''N1. współliniowość punktów''' (rzuty punktów leżących na prostej będą leżały na rzucie tej prostej), | |||
'''N2. przynależności elementów''' (jeżeli punkt leży na prostej, to rzut tego punktu leży na rzucie tej prostej), | |||
'''N3. równoległość prostych''' (rzutami prostych równoległych są proste równoległe lub punkty), | |||
'''N4. stosunek długości odcinków równoległych do siebie, nierównoległych do kierunku rzutowania''', (jeżeli długości odcinków równoległych pozostają w określonym stosunku do siebie to długości ich rzutów pozostają w stosunku identycznym), | |||
'''N5. stosunek podziału odcinka''' (jeżeli punkt A dzieli odcinek w określonym stosunku, to rzut punktu A' dzieli rzut tego odcinka w takim samym stosunku), | |||
'''N6. długość odcinków równoległych do rzutni''' (długość odcinka równoległego do rzutni jest taka sama jak długość rzutu tego odcinka), | |||
'''N7. kąt o obu ramionach równoległych do rzutni''' (wielkość kąta, którego obydwa ramiona są równoległe do rzutni jest taka sama jak wielkość rzutu tego kąta), | |||
'''N8. związki miarowe w płaszczyźnie równoległej do rzutni''' (długości odcinków, kąty oraz wielkości figur leżących na płaszczyźnie równoległej do rzutni zachowują się po dokonaniu operacji rzutowania). | |||
Niezmienniki rzutowania równoległego stanowią własności o charakterze podstawowym, które będą wykorzystywane do zapisu konstrukcji technicznych na płaszczyźnie. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd9.png]] | |||
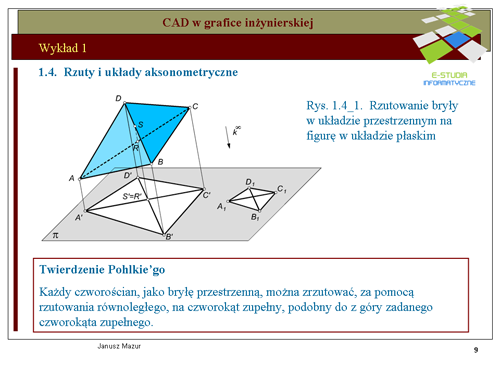
|valign="top"|Znany z geometrii elementarnej układ osi współrzędnych, zwany układem kartezjańskim, jest układem przestrzennym i składa się z osi <math> x, y, z</math> oraz początku układu współrzędnych 0. Osie przecinają się w punkcie początkowym każdej z nich pod kątami <math>90^o\,</math> względem siebie. Umieszczony w takim układzie punkt <math>P\,</math> będzie miał współrzędne <math>P(x_o, y_o, z_o)</math>. Analogicznie można zdefiniować położenie wektora i innych elementów w przestrzeni. Rzuty aksonometryczne są formą rzutów równoległych, które pozwalają przetransponować układ przestrzenny <math>0xyz</math> na układ płaski, a więc układ umożliwiający odwzorowanie tworów przestrzennych na płaszczyźnie. Takim zagadnieniem jesteśmy zainteresowani z punktu widzenia graficznego zapisu konstrukcji. Rozwijając teorię rzutowania równoległego przyjmiemy twierdzenie '''Pohlke'go''', które otworzy możliwości wyodrębnionego zapisu tworów przestrzennych zwanego '''rzutem aksonometrycznym'''. Twierdzenie to umożliwia przenoszenie brył przestrzennych do zupełnie dowolnych układów płaskich zwanych układami aksonometrycznymi. Stanowi to dla inżyniera źródło możliwości różnorodnego eksponowania swoich twórczych projektów. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd10.png]][[Grafika:CWGI_M1_Slajd11.png]][[Grafika:CWGI_M1_Slajd12.png]] | |||
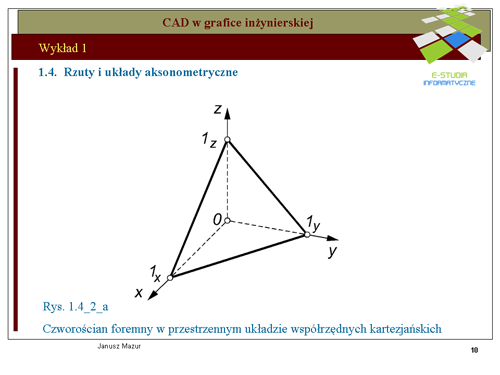
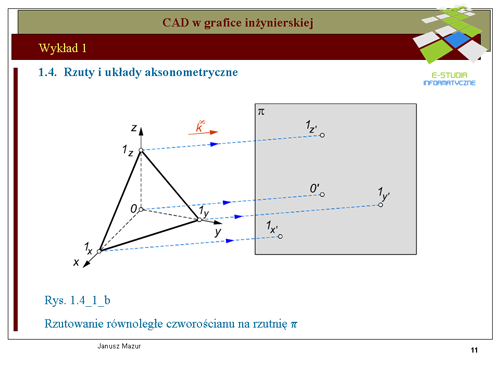
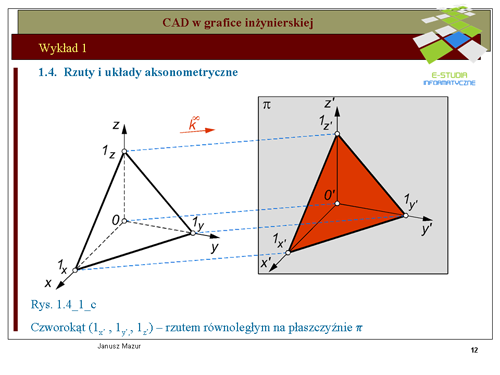
|valign="top"|Przyjmując do wiadomości ustalenia twierdzenia Pohlke'go można układ współrzędnych kartezjańskich, za pomocą rzutu równoległego, przetransponować na dowolny układ płaski. Ilustruje to rys.1.4a- 1.4c. Początek <math>0\,</math> układu <math>0xyz\,</math> oraz punkty jednostkowe <math>1x, 1y, 1z</math>, tworzą, bowiem czworościan 01x1y1z, który w myśl twierdzenia Pohlke’go można odwzorować na czworokąt zupełny <math>0’1x’1y’1z’</math>, podobny do z góry zadanego czworokąta zupełnego (czyli czworokąt dowolny). | |||
Ma to fundamentalne znaczenie dla konstruktorów. Oznacza, iż odwzorowanie przestrzennych brył na płaszczyznę można dokonywać w dowolnych układach równoległego rzutu aksonometrycznego, pod warunkiem opisania podstawowych jego parametrów, do których należą rozmieszczenie rzutów osi układu kartezjańskiego oraz tzw. skrótów aksonometrycznych wynikających z rzutowania równoległego układu. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:CWGI_M1_Slajd13.png]] | |||
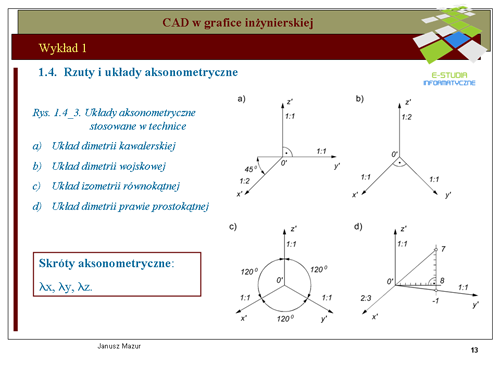
|valign="top"| Dla potrzeb graficznego zapisu konstrukcji, w wyniku doświadczeń praktycznych, zaproponowano cztery najbardziej używane i przydatne w technice układy aksonometryczne. Na rys. 1.4_3 przedstawiono praktyczne układy aksonometryczne o następujących parametrach wynikających z rzutowania równoległego: | |||
a) układ dimetrii kawalerskiej <math>(\lambda_x=1:2, y=1:1, z=1:1)</math>, | |||
b) układ dimetrii wojskowej (x'=1:1, y'=1:1, z'=1:2), | |||
c) układ izometrii równokątnej (x =1:1, y=1:1, z=1:1), | |||
d) układ dimetrii prawie prostokątnej (x'=2:3, y'=1:1, z'=1:1). | |||
W układzie dimetrii kawalerskiej osie y' i z' położone są względem siebie pod kątem 90o . Oś x' tworzy kąt 135o z osiami y' i z'. Układ umożliwia zapis bez zniekształceń w pł. (0, y', z'). | |||
W układzie dimetrii wojskowej oś z' układu jest pionowa, skrót zmniejsza wymiary w tym kierunku dwukrotnie. Osie x', y' tworzą kąt 135o z osią z'. Skróty nie zmieniają wymiarów w kierunku tych osi. | |||
Układ izometrii równokątnej jest układem regularnym. Osie x', y', z' tworzą kąt 120o względem siebie. Skróty nie zmieniają wymiarów w każdej osi. | |||
Tworzenie trzech pierwszych układów nie sprawia żadnych problemów. Komentarza wymaga tworzenie układu dimetrii prawie prostokątnej. Oś z' jest osią pionową. Pozostałe osie x' i y' tworzymy w sposób następujący: | |||
1. na pomocniczej linii poziomej odmierzamy osiem odcinków jednostkowych otrzymując na niej | |||
punkt, przez który prowadzimy pomocniczą prostą pionową. | |||
2. odmierzając następnie na tej prostej w kierunku do góry 7 odcinków jednostkowych oraz 1 w dół | |||
otrzymamy dwa punkty, | |||
3. łącząc otrzymane punkty z środkiem układu wyznaczymy położenie osi x' i y'. | |||
Rysowanie technicznych obiektów przestrzennych w rzutach aksonometrycznych pozwala przygotować zapis konstrukcji, który może być zrozumiały dla każdego czytelnika oraz przydatny do dalszych zapisów technicznych. | |||
Wersja z 11:24, 7 sie 2006