PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 14: | Linia 14: | ||
W elektrotechnice najczęściej używane jest jednostronne przekształcenie Laplace’a, określone parą równań: | W elektrotechnice najczęściej używane jest jednostronne przekształcenie Laplace’a, określone parą równań: | ||
: <math>F(s)=L \left \{f(t) \right \}=\int_{0}^{\infty} f(t)e^{-st} dt</math> | |||
: <math>f(t)=L^{-1} \left \{F(s) \right \}=\frac{1}{2\pi \cdot j}\int_{c-j\omega}^{c+j\omega} F(s)e^{st} ds</math> | |||
<math>f(t)=L^{-1} \left \{F(s) \right \}=\frac{1}{2\pi \cdot j}\int_{c-j\omega}^{c+j\omega} F(s)e^{st} ds</math> | |||
w których c jest bliżej nieokreśloną stałą warunkującą położenie granic całkowania w obszarze zbieżności transformaty. Pierwsze z równań definiuje '''proste przekształcenie''' Laplace’a przyporządkowujące oryginałowi transformatę zmiennej zespolonej s, a drugie '''przekształcenie odwrotne''' dokonujące transformacji odwrotnej, czyli wyznaczające funkcję oryginału na podstawie F(s). Zakładamy przy tym, że funkcja f(t) jest funkcją czasu, zadaną dla t>0 i równą 0 dla t<0 oraz, że nie rośnie szybciej niż funkcja wykładnicza. Proste przekształcenie Laplace’a określone wzorem ze slajdu 2 dokonuje transformacji funkcji czasu f(t) na funkcję F(s) zmiennej zespolonej s. Przekształcenie odwrotne określone wzorem ze slajdu 2 dokonuje transformacji funkcji zespolonej F(s) na funkcję czasu f(t). Wzór ten pełni jedynie rolę definicji i w praktyce nie używa się go do wyznaczania transformaty odwrotnej, wykorzystując w zamian własności transformat Laplace’a. | w których c jest bliżej nieokreśloną stałą warunkującą położenie granic całkowania w obszarze zbieżności transformaty. Pierwsze z równań definiuje '''proste przekształcenie''' Laplace’a przyporządkowujące oryginałowi transformatę zmiennej zespolonej s, a drugie '''przekształcenie odwrotne''' dokonujące transformacji odwrotnej, czyli wyznaczające funkcję oryginału na podstawie F(s). Zakładamy przy tym, że funkcja f(t) jest funkcją czasu, zadaną dla t>0 i równą 0 dla t<0 oraz, że nie rośnie szybciej niż funkcja wykładnicza. Proste przekształcenie Laplace’a określone wzorem ze slajdu 2 dokonuje transformacji funkcji czasu f(t) na funkcję F(s) zmiennej zespolonej s. Przekształcenie odwrotne określone wzorem ze slajdu 2 dokonuje transformacji funkcji zespolonej F(s) na funkcję czasu f(t). Wzór ten pełni jedynie rolę definicji i w praktyce nie używa się go do wyznaczania transformaty odwrotnej, wykorzystując w zamian własności transformat Laplace’a. | ||
|} | |} | ||
| Linia 29: | Linia 25: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd3.png]] | ||
|valign="top"| | |valign="top"|Z wielu istniejących własności przekształcenia Laplace’a ograniczymy się tutaj do kilku podstawowych, których znajomość jest konieczna do określenia stanów nieustalonych w obwodach RLC. | ||
Z wielu istniejących własności przekształcenia Laplace’a ograniczymy się tutaj do kilku podstawowych, których znajomość jest konieczna do określenia stanów nieustalonych w obwodach RLC. | |||
''Liniowość przekształcenia'' | ''Liniowość przekształcenia'' | ||
Jeśli współczynniki <math>a_1</math> i <math>a_2</math> są dowolnymi stałymi to | Jeśli współczynniki <math>a_1</math> i <math>a_2</math> są dowolnymi stałymi to | ||
<math>L \left[a_1 f_1(t)+a_2 f_2(t)\right]=a_1 F_1(s)+a_2 F_2(s)</math> | <math>L \left[a_1 f_1(t)+a_2 f_2(t)\right]=a_1 F_1(s)+a_2 F_2(s)</math> | ||
<math>L^{-1} \left[a_1 F_1(s)+a_2 F_2(s)\right]=a_1 f_1(t)+a_2 f_2(t)</math> | <math>L^{-1} \left[a_1 F_1(s)+a_2 F_2(s)\right]=a_1 f_1(t)+a_2 f_2(t)</math> | ||
gdzie symbole <math>L</math> i <math>L^{-1}</math> oznaczają odpowiednio transformaty: prostą i odwrotną Laplace’a. Z własności liniowości przekształcenia wynika, że przekształcenie Laplace’a spełnia zasadę superpozycji. | gdzie symbole <math>L</math> i <math>L^{-1}</math> oznaczają odpowiednio transformaty: prostą i odwrotną Laplace’a. Z własności liniowości przekształcenia wynika, że przekształcenie Laplace’a spełnia zasadę superpozycji. | ||
''Transformata pochodnej funkcji czasu'' | ''Transformata pochodnej funkcji czasu'' | ||
Transformata pochodnej funkcji czasu spełnia relację | Transformata pochodnej funkcji czasu spełnia relację | ||
: <math>L \left[ \frac{df(t)}{dt} \right]=sF(s)-f(0^{+})</math> | : <math>L \left[ \frac{df(t)}{dt} \right]=sF(s)-f(0^{+})</math> | ||
W której <math>f(0^{+})</math> oznacza wartość początkową funkcji f(t). Mnożenie funkcji F(s) przez zmienną zespoloną s odpowiada w dziedzinie czasu różniczkowaniu funkcji. Stąd operator s nazywany jest operatorem różniczkowania. | W której <math>f(0^{+})</math> oznacza wartość początkową funkcji f(t). Mnożenie funkcji F(s) przez zmienną zespoloną s odpowiada w dziedzinie czasu różniczkowaniu funkcji. Stąd operator s nazywany jest operatorem różniczkowania. | ||
|} | |||
<hr width="100%"> | |||
''Transformata całki funkcji czasu'' | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd3.png]] | |||
|valign="top"|''Transformata całki funkcji czasu'' | |||
Transformata całki funkcji czasu spełnia relację | Transformata całki funkcji czasu spełnia relację | ||
: <math>L \left[\int_{0}^{t}f(\tau)d\tau \right]=\frac{F(s)}{s}</math> | : <math>L \left[\int_{0}^{t}f(\tau)d\tau \right]=\frac{F(s)}{s}</math> | ||
Pomnożenie funkcji F(s) przez 1/s odpowiada w dziedzinie czasu całkowaniu funkcji. Stąd operator <math>s^{-1}\,</math> jest nazywany również operatorem całkowania. | Pomnożenie funkcji F(s) przez 1/s odpowiada w dziedzinie czasu całkowaniu funkcji. Stąd operator <math>s^{-1}\,</math> jest nazywany również operatorem całkowania. | ||
''Transformata splotu'' | ''Transformata splotu'' | ||
| Linia 74: | Linia 62: | ||
Splot stanowi ważne pojęcie w teorii obwodów, gdyż za jego pośrednictwem określa się odpowiedzi czasowe obwodów rzeczywistych RLC. Splot dwu funkcji czasu <math>f_1(t)</math> i <math>f_2(t)</math> oznaczony w postaci <math>f_1(t)*f_1(t)</math> jest zdefiniowany w następujący sposób | Splot stanowi ważne pojęcie w teorii obwodów, gdyż za jego pośrednictwem określa się odpowiedzi czasowe obwodów rzeczywistych RLC. Splot dwu funkcji czasu <math>f_1(t)</math> i <math>f_2(t)</math> oznaczony w postaci <math>f_1(t)*f_1(t)</math> jest zdefiniowany w następujący sposób | ||
: <math>f_1(t)*f_1(t)=\int_{0}^{t} f_1(\tau)f_2({t-\tau})d\tau=</math> | |||
<math>f_1(t)*f_1(t)=\int_{0}^{t} f_1(\tau)f_2({t-\tau})d\tau=</math> | |||
: <math>=\int_{0}^{t}f_1({t-\tau})f_2(\tau)d\tau</math> | : <math>=\int_{0}^{t}f_1({t-\tau})f_2(\tau)d\tau</math> | ||
Transformata Laplace’a splotu jest równa zwykłemu iloczynowi transformat poszczególnych funkcji tworzących splot | Transformata Laplace’a splotu jest równa zwykłemu iloczynowi transformat poszczególnych funkcji tworzących splot | ||
: <math>L \left[f_1(t)*f_2(t) \right]=F_1(s) \cdot F_2(s)</math> | : <math>L \left[f_1(t)*f_2(t) \right]=F_1(s) \cdot F_2(s)</math> | ||
Powyższa własność nosi w matematyce nazwę twierdzenia Borela. Zauważmy, że mnożenie splotowe dwu funkcji w dziedzinie czasu odpowiada zwykłemu mnożeniu ich transformat w dziedzinie częstotliwości. Własność ta jest szczególnie wygodna w analizie obwodów zarówno w stanie ustalonym jak i nieustalonym. Zamiast żmudnych operacji w dziedzinie czasu wykonuje się transformację Laplace’a funkcji czasowych a następnie wszystkie operacje wykonuje na transformatach. | Powyższa własność nosi w matematyce nazwę twierdzenia Borela. Zauważmy, że mnożenie splotowe dwu funkcji w dziedzinie czasu odpowiada zwykłemu mnożeniu ich transformat w dziedzinie częstotliwości. Własność ta jest szczególnie wygodna w analizie obwodów zarówno w stanie ustalonym jak i nieustalonym. Zamiast żmudnych operacji w dziedzinie czasu wykonuje się transformację Laplace’a funkcji czasowych a następnie wszystkie operacje wykonuje na transformatach. | ||
|} | |} | ||
Wersja z 11:23, 25 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
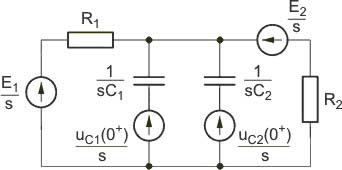
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
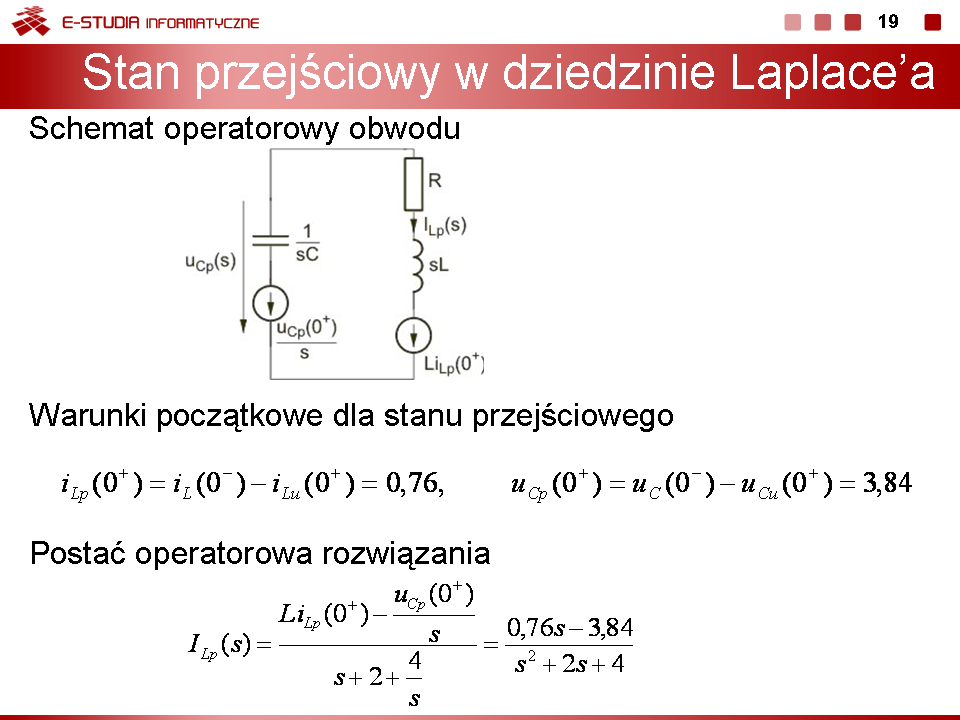
3) Stan przejściowy po przełączeniu
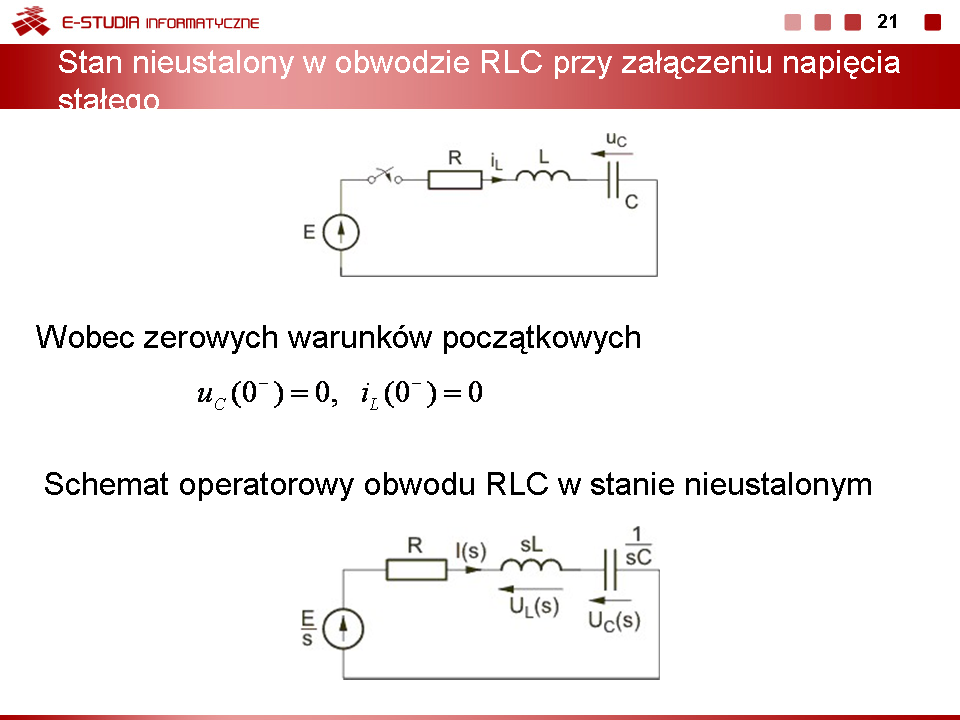
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
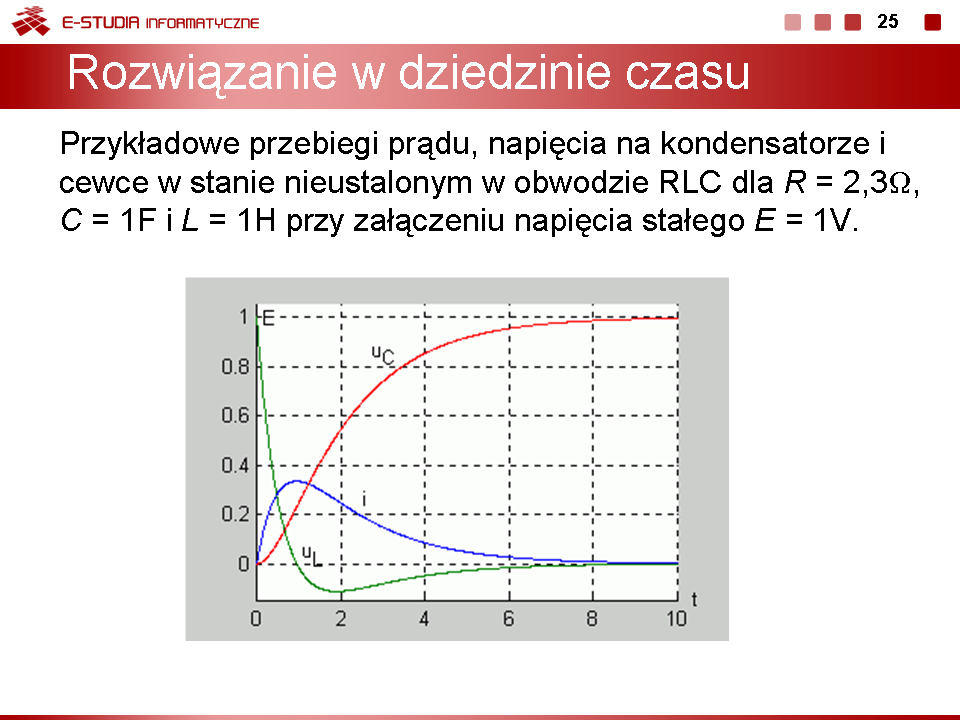
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|

|
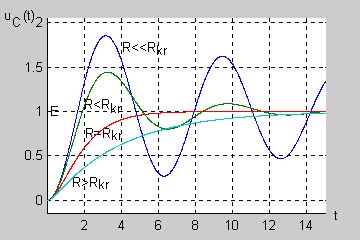
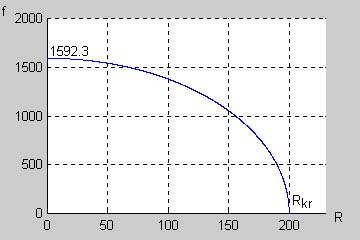
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |