PEE Zadania do samodzielengo rozwiązania

Przykłady zadań do samodzielengo rozwiązania

Zad 1

Obliczyć rezystancję z zacisków A-B obwodu.

Dane:

$R_1=3\mathrm{\Omega }$

$R_2=7\mathrm{\Omega }$

$R_3=20\mathrm{\Omega }$

$R_4=5\mathrm{\Omega }$

$R_5=10\mathrm{\Omega }$

$R_6=10\mathrm{\Omega }$

Odp. $R_{AB}=5,26\mathrm{\Omega }$

---

Zad. 2

Obliczyć rezystancję z zacisków A-B obwodu.

a)

Dane:

$R_1=2\mathrm{\Omega }$

$R_2=5\mathrm{\Omega }$

$R_3=1\mathrm{\Omega }$

$R_4=3\mathrm{\Omega }$

$R_5=2\mathrm{\Omega }$

$R_6=1\mathrm{\Omega }$

$R_7=1\mathrm{\Omega }$

$R_8=2\mathrm{\Omega }$

Odp. $R_{AB}=2,61\mathrm{\Omega }$

---

Zad. 3

Metodą praw Kirchhoffa obliczyć prądy w obwodzie.

a)

Dane:

$I=5A$

$E=10V$

$R_1=1\mathrm{\Omega }$

$R_2=5\mathrm{\Omega }$

$R_3=10\mathrm{\Omega }$

Odp. $I_1=4A$, $I_2=1A$

---

Zad. 4

Wyznaczyć rozpływy prądów w obwodzie. Sporządzić bilans mocy.

a)

Dane:

$e(t)=10\sqrt{2}sin(t+90^{\circ })V$

$R_1=2\mathrm{\Omega }$

$R_2=1\mathrm{\Omega }$

$C=0,5F$

$L=1H$

Odp. $I=(0,5+j3,5)A$, $U_{RLC}=(-1+j3)A$, $I_1=(9+j1)A$, $I_2=(-1,5-j0,1)A$, $I_3=(-1+j3)A$,

$P_{odb}=35W$, $Q_{odb}=5var$, $S_{gen}=(35+j5)VA$

---

Zad. 5

Narysować wykres wektorowy dla obwodu.

a)

---

Zad. 6

Obliczyć prądy w obwodach stosując metodę:

a) potencjałów węzłowych

Dane:

$I_1=5A$

$I_2=2A$

$E=10V$

$R_1=5\mathrm{\Omega }$

$R_2=5\mathrm{\Omega }$

$R_3=5\mathrm{\Omega }$

$R_4=10\mathrm{\Omega }$

Odp. $I_{R2}=2,75A$, $I_{R3}=2,25A$, $I_{R4}=0,75A$

b) metodę oczkową

Dane:

$E_1=10V$

$E_2=10V$

$E_3=20V$

$R_1=10\mathrm{\Omega }$

$R_2=10\mathrm{\Omega }$

$R_3=5\mathrm{\Omega }$

$R_4=5\mathrm{\Omega }$

$R_4=5\mathrm{\Omega }$

Odp. $I_{R1}=-1,68A$, $I_{R2}=-0,54A$, $I_{R3}=-0,29A$, $I_{R4}=-0,25A$, $I_{R5}=-1,97A$

---

Zad. 7

Stosując metodę Thevenina wyznaczyć prąd $I_x$ w obwodzie.

Dane:

$E_1=20V$

$E_2=5V$

$R_1=10\mathrm{\Omega }$

$R_2=20\mathrm{\Omega }$

$R_3=10\mathrm{\Omega }$

$R_4=10\mathrm{\Omega }$

$R_5=5\mathrm{\Omega }$

Odp. $I_x=0,5A$

---

Zad. 8

Obliczyć prądy i bilans mocy w obwodzie.

a)

Dane:

$i(t)=10\sqrt{2}sin(t+45^{\circ })A$

$R=5\mathrm{\Omega }$

$L_1=2H$

$L_1=1H$

$C_1=0,5F$

$C_1=0,5F$

Odp. $I=(2,72+j4,08)A$, $I_2=(-2,72-j4,08)A$, $I_3=(1,67-j1,09)A$, $I_4=(5,44+j8,16)A$,

$P_{odb}=19,225W$, $Q_{odb}=-96,125var$, $S_{gen}=(19,225-j96,125)VA$

---

Zad. 9

Wyeliminować sprzężenia w obwodzie.

a)

Odp.

---

Zad. 10

Obliczyć rozpływy prądów w obwodzie, napięcia na cewkach sprzężonych oraz sporządzić bilans mocy.

Dane:

$e(t)=100\sqrt{2}sin\omega t$

$R_1=10\mathrm{\Omega }$

$R_2=5\mathrm{\Omega }$

$X_{L1}=25\mathrm{\Omega }$, $X_{L2}=40\mathrm{\Omega }$, $X_M=10\mathrm{\Omega }$,

Odp. $I=(3,19-j8,03)A$, $I_1=(2,2-j4,52)A$, $I_2=(0,99-j3,51)A$, $U_{L1}=(77,96+j45,21)V$, $U_{L2}=(95,05+j17,53)V$, $P_{odb}=319,35W$, $Q_{odb}=802,76var$, Parser nie mógł rozpoznać (błąd składni): {\displaystyle S_{źr}=(319,35+j802,76)\, VA}

---

Zad. 11

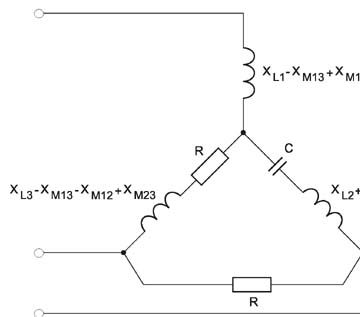
Obliczyć moduły prądów liniowych odbiornika trójfazowego przedstawionego na rysunku.

Dane:

$R=10\mathrm{\Omega }$

$X_C=10\mathrm{\Omega }$

$X_M=10\mathrm{\Omega }$

$X_{L1}=20\mathrm{\Omega }$

$X_{L2}=20\mathrm{\Omega }$

Odp. $|I_A|=34,5A$, $|I_B|=24A$, $|I_C|=36,8A$

---

Zad. 12

Wyznaczyć opis stanowy obwodu.

Dane:

$R_1=2\mathrm{\Omega }$

$R_2=1\mathrm{\Omega }$

$C=1F$

$L_1=1H$

$L_2=2H$

$M=1H$

Odp. $|I_A|=34,5A$, $|I_B|=24A$, $|I_C|=36,8A$