PEE Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 377: | Linia 377: | ||
Jednostką stałej czasowej jest sekunda (jednostką indukcyjności jest <math>1H = 1\Omega s</math> a jednostką rezystancji <math>1\Omega</math>). Łatwo wykazać, że po upływie trzech stałych czasowych <math>(t=3\tau )</math> prąd cewki uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po 5 stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony. | Jednostką stałej czasowej jest sekunda (jednostką indukcyjności jest <math>1H = 1\Omega s</math> a jednostką rezystancji <math>1\Omega</math>). Łatwo wykazać, że po upływie trzech stałych czasowych <math>(t=3\tau )</math> prąd cewki uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po 5 stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony. | ||
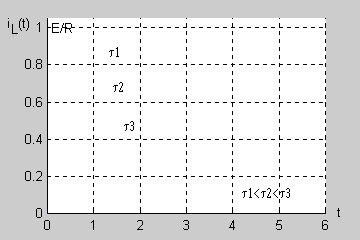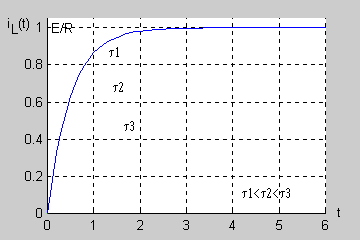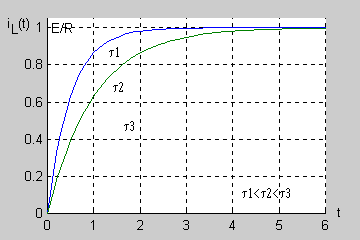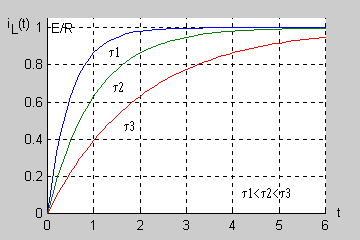
Na rysunku przedstawiono przebiegi prądu cewki dla różnych wartości stałej czasowej | Na rysunku poniżej przedstawiono przebiegi prądu cewki dla różnych wartości stałej czasowej | ||
[[Grafika:PEE_M7_anim_13.gif]] | |||
Jest to przebieg typu wykładniczego, w którym stan przejściowy trwa tym dłużej im dłuższa jest stała czasowa. Praktycznie po 5 stałych czasowych stan przejściowy w obwodzie zanika przechodząc w stan ustalony. | Jest to przebieg typu wykładniczego, w którym stan przejściowy trwa tym dłużej im dłuższa jest stała czasowa. Praktycznie po 5 stałych czasowych stan przejściowy w obwodzie zanika przechodząc w stan ustalony. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|Stałą czasową obwodu RL można wyznaczyć na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i indukcyjności. Zauważmy, że dla prąd cewki przyjmuje wartość | |Stałą czasową obwodu RL można wyznaczyć na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i indukcyjności. Zauważmy, że dla prąd cewki przyjmuje wartość | ||
| Linia 392: | Linia 398: | ||
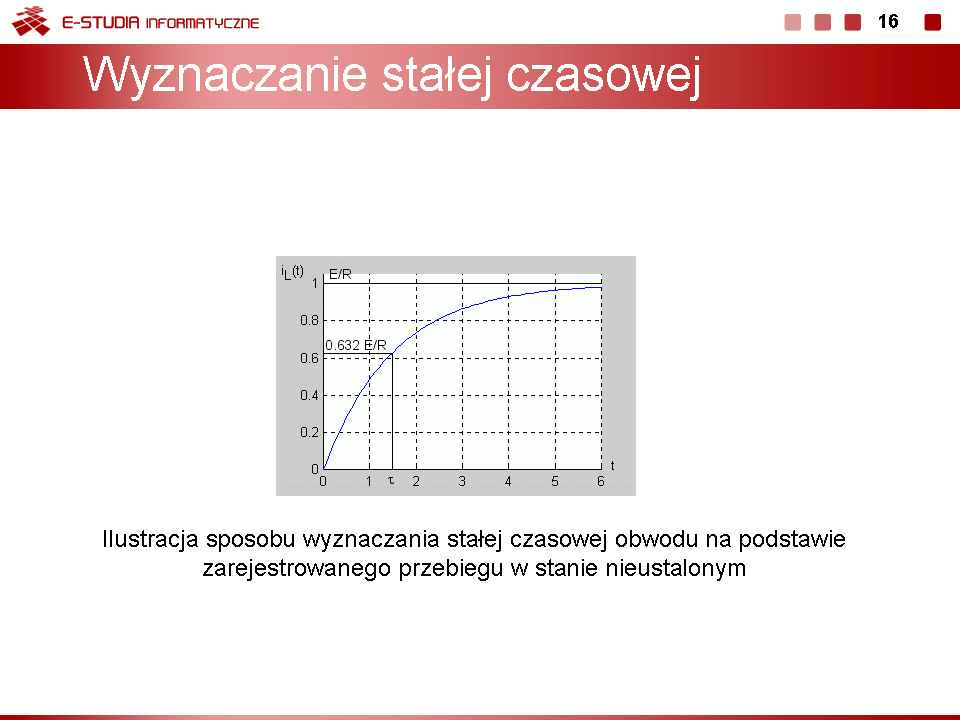
Oznacza to, że wartość prądu <math>i_L(t)|_{t=\tau}=0,632\frac{E}{R}</math> wyznacza na osi odciętych wartość stałej czasowej. Sposób wyznaczania stałej czasowej zilustrowany jest na rysunku | Oznacza to, że wartość prądu <math>i_L(t)|_{t=\tau}=0,632\frac{E}{R}</math> wyznacza na osi odciętych wartość stałej czasowej. Sposób wyznaczania stałej czasowej zilustrowany jest na rysunku | ||
[[Grafika:PEE_M7_anim_13_b.gif]] | |||
|} | |} | ||
| Linia 406: | Linia 412: | ||
Przebieg napięcia na cewce w stanie nieustalonym w obwodzie szeregowym RL przedstawiono na rysunku | Przebieg napięcia na cewce w stanie nieustalonym w obwodzie szeregowym RL przedstawiono na rysunku | ||
[[Grafika:PEE_M7_anim_14.gif]] | |||
Napięcie na rezystorze R, jak wynika z prawa Ohma, jest proporcjonalne do prądu | Napięcie na rezystorze R, jak wynika z prawa Ohma, jest proporcjonalne do prądu | ||
| Linia 502: | Linia 510: | ||
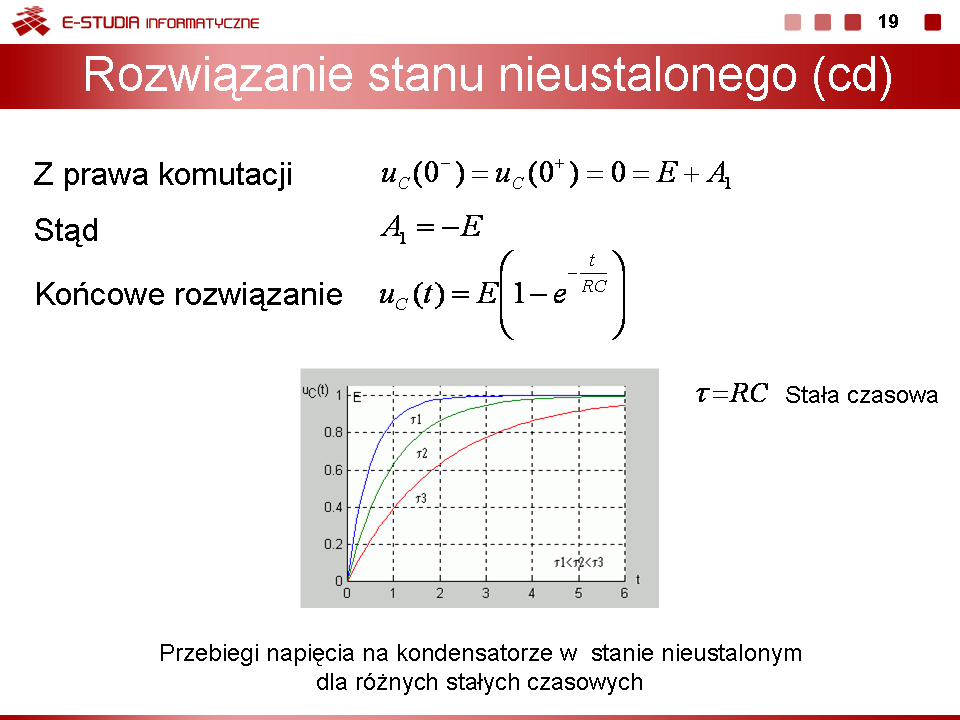
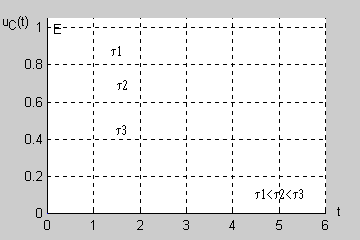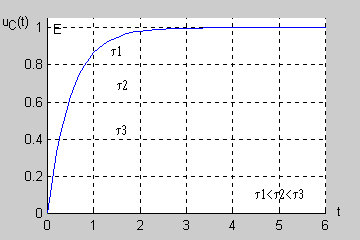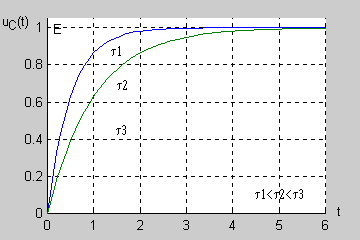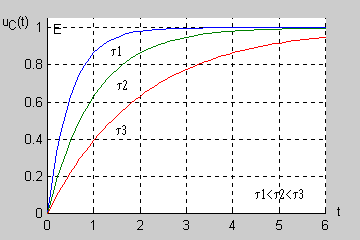
Jak łatwo sprawdzić podstawową jednostką stałej czasowej w obwodzie RC jest również sekunda (jednostką rezystancji jest <math>1\Omega = 1V/A</math>, a jednostką pojemności jest <math>1F = 1As/V</math>). Na rysunku przedstawiono przebiegi napięcia na kondensatorze w stanie nieustalonym <math>u_C(t)=E(1-e^{-\frac{t}{\tau}})</math> dla różnych wartości stałej czasowej. | Jak łatwo sprawdzić podstawową jednostką stałej czasowej w obwodzie RC jest również sekunda (jednostką rezystancji jest <math>1\Omega = 1V/A</math>, a jednostką pojemności jest <math>1F = 1As/V</math>). Na rysunku przedstawiono przebiegi napięcia na kondensatorze w stanie nieustalonym <math>u_C(t)=E(1-e^{-\frac{t}{\tau}})</math> dla różnych wartości stałej czasowej. | ||
[[Grafika:PEE_M7_anim_17.gif]] | |||
Im dłuższa stała czasowa tym dłużej trwa stan przejściowy w obwodzie (zanikanie zmian napięcia do zera). | Im dłuższa stała czasowa tym dłużej trwa stan przejściowy w obwodzie (zanikanie zmian napięcia do zera). | ||
| Linia 527: | Linia 537: | ||
[[Grafika: | [[Grafika:PEE_M7_anim_14.gif]] | ||
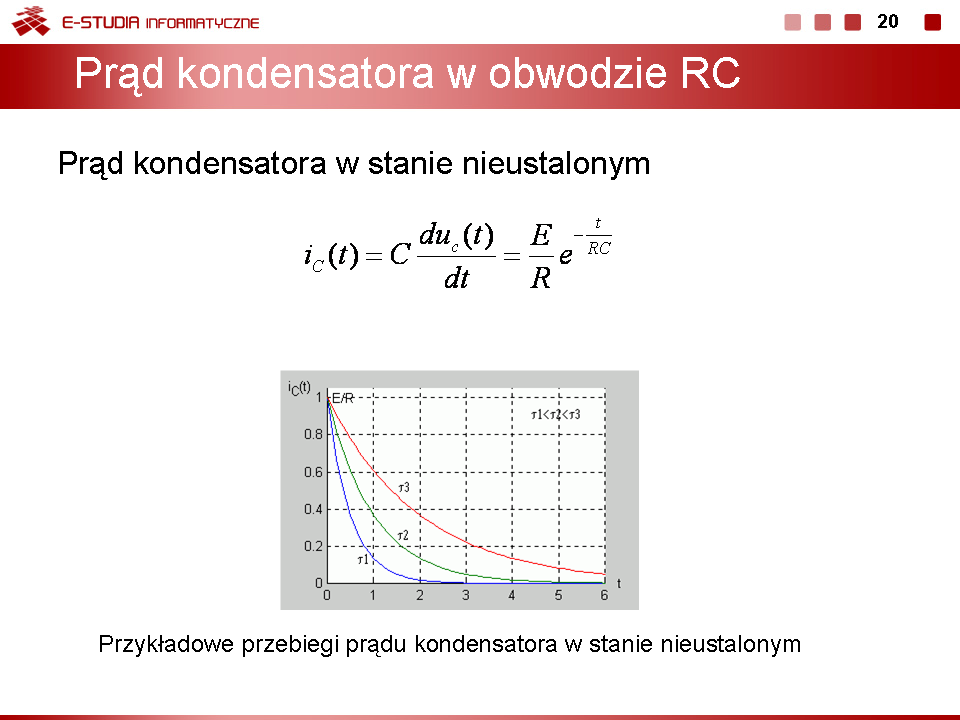
W chwili komutacji występuje skokowa zmiana wartości prądu (prąd kondensatora nie jest objęty komutacyjnym prawem ciągłości). Przebieg prądu kondensatora dąży do wartości ustalonej zerowej (w stanie ustalonym kondensator stanowi przerwę dla prądu). Stała czasowa zmian tego prądu jest identyczna jak napięcia i równa <math>\tau=RC</math>. | W chwili komutacji występuje skokowa zmiana wartości prądu (prąd kondensatora nie jest objęty komutacyjnym prawem ciągłości). Przebieg prądu kondensatora dąży do wartości ustalonej zerowej (w stanie ustalonym kondensator stanowi przerwę dla prądu). Stała czasowa zmian tego prądu jest identyczna jak napięcia i równa <math>\tau=RC</math>. | ||
Wersja z 08:58, 3 sie 2006

|
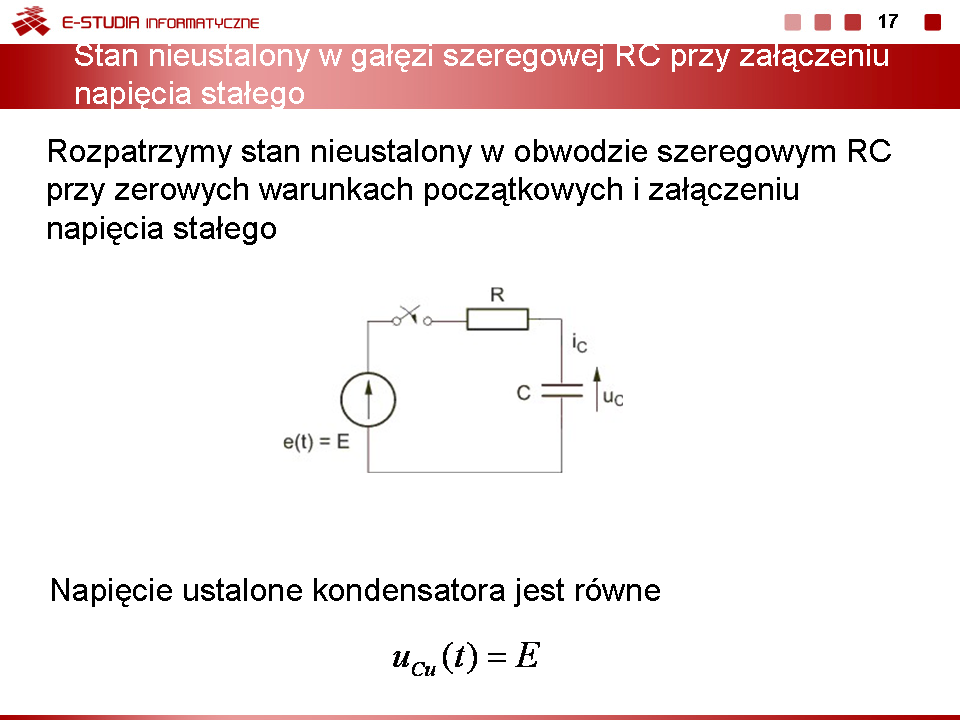
Metoda równań różniczkowych w rozwiązaniu stanu nieustalonego w obwodach elektrycznych |

|
Przykład
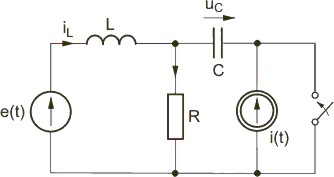
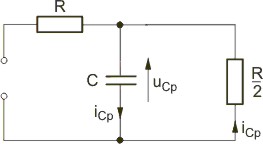
Napisać układ równań stanu dla obwodu elektrycznego przedstawionego na rysunku |
| Stałą czasową obwodu RL można wyznaczyć na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i indukcyjności. Zauważmy, że dla prąd cewki przyjmuje wartość
|
| Łatwo wykazać, że po upływie 3 stałych czasowych ( ) napięcie uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony.
Stałą czasową można wyznaczyć bezpośrednio na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i pojemności, podobnie jak to miało miejsce w przypadku obwodu RL. |
| Zadania sprawdzające
Zadanie 7.1 Wyznaczyć warunki początkowe w obwodzie przedstawionym na rysunku. Parametry elementów obwodu są następujące: Rozwiązanie Warunki początkowe dotyczą stanu ustalonego przed przełączeniem, w którym w obwodzie działają oba źródła wymuszające. Stosując metodę symboliczną analizy obwodu otrzymujemy
|

|
Równania obwodu w stanie ustalonym
Warunki początkowe:
|
| Zadanie 7.2
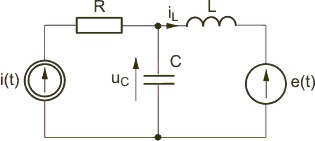
Napisać równanie stanu dla obwodu o strukturze przedstawionej na rysunku Rozwiązanie Z praw Kirchhoffa napisanych dla obwodu z rysunku wynika
Rozwiązanie Warunki początkowe w obwodzie wynikają ze stanu ustalonego obwodu przed przełączeniem, który wobec wymuszenia stałego ma postać uproszczoną przedstawioną na rysunku Schemat obwodu w stanie ustalonym przed przełączeniem dla wymuszenia stałego
Schemat obwodu w stanie ustalonym po przełączeniu
Schemat obwodu w stanie przejściowym po przełączeniu
Postać ostateczna rozwiązania:
|