PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 551: | Linia 551: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd22.png]] | ||
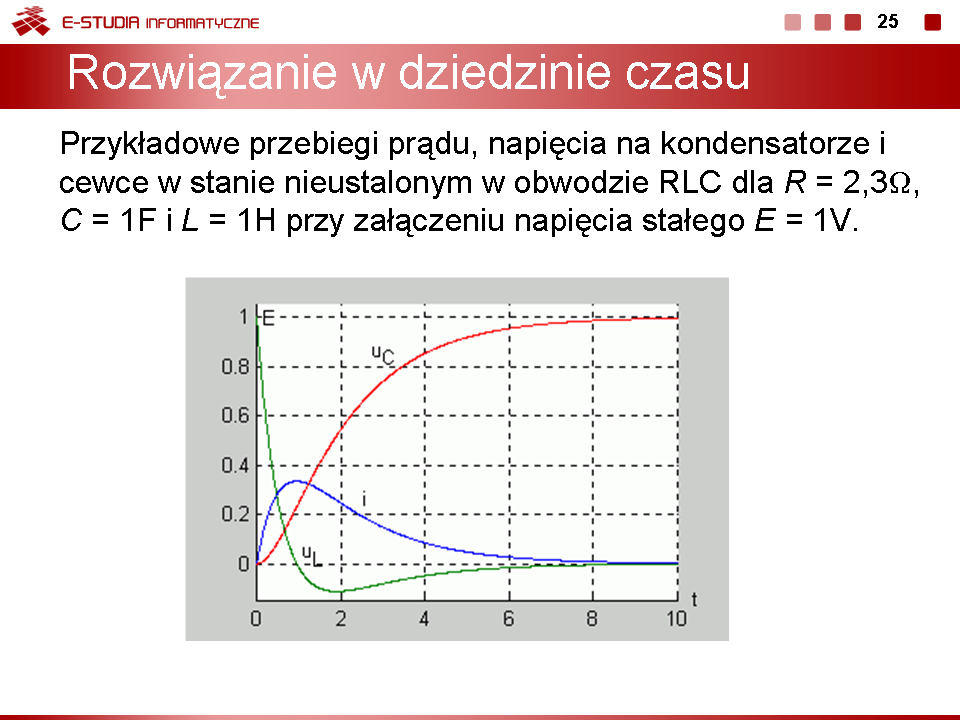
|valign="top"|Na | |valign="top"|Na slajdzie 22 przedstawiono przebiegi prądu, napięcia na kondensatorze i cewce w stanie nieustalonym w obwodzie RLC dla <math>R=2,3\Omega</math>, <math>C=1F\,</math>, <math>L=1H\,</math>.przy załączeniu napięcia stałego <math>E=1V\,</math>. Dla przyjętych wartości parametrów elementów mamy do czynienia z przypadkiem aperiodycznym. | ||
Prąd w obwodzie oraz napięcie na kondensatorze zachowują ciągłość i spełniają prawa komutacji. W stanie ustalonym prąd w obwodzie nie płynie (kondensator w stanie ustalonym stanowi przerwę) a napięcie na kondensatorze przyjmuje wartość napięcia zasilającego E. Zauważmy ponadto, że wartości maksymalnej prądu odpowiada zerowa wartość napięcia na cewce (<math>u_L(t)=L\frac{di}{dt}</math>). W chwili, gdy napięcie na cewce osiąga wartość maksymalną ujemną, w przebiegu napięcia na kondensatorze można zauważyć punkt przegięcia. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd23.png]] | |||
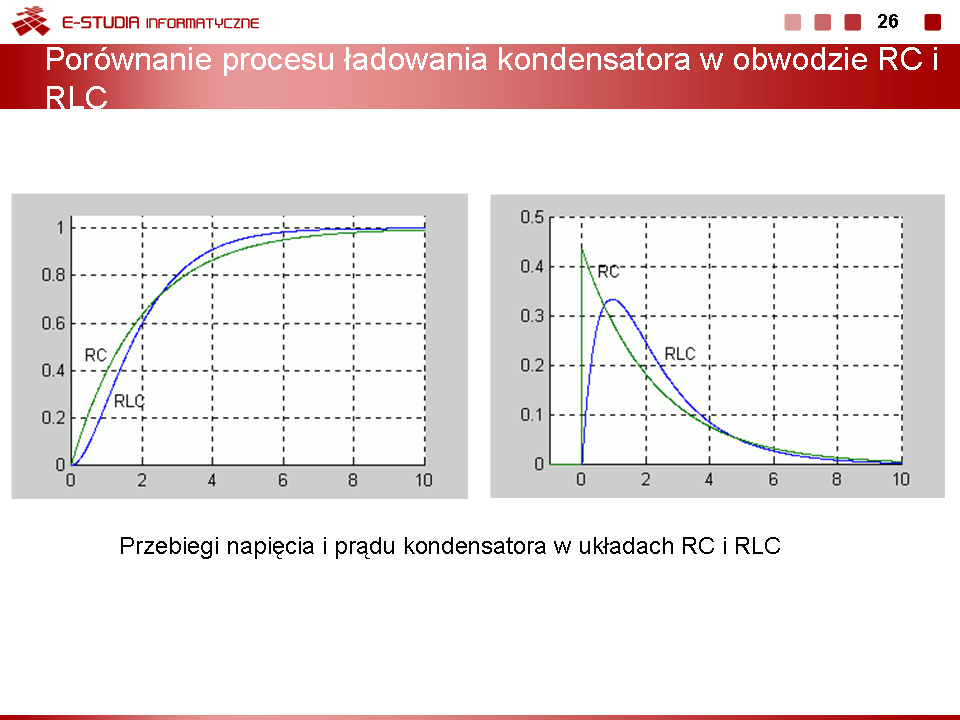
|valign="top"|Interesujące jest porównanie procesu ładowania kondensatora w obwodzie RLC w stanie aperiodycznym oraz w obwodzie RC. Napięcie i prąd kondensatora w obwodzie RC, jak zostało pokazane w lekcji jedenastej opisane są funkcjami <math>u_C(t)=E(1-e^{-\frac{t}{RC}})</math>, <math>i_C(t)=\frac{E}{R}e^{-\frac{t}{RC}}</math>. Na slajdzie 23 przedstawiono przebiegi napięcia na kondensatorze oraz prądu. | |||
W napięciu <math>u_C(t)</math> w obwodzie RLC widoczny jest łagodnie narastający przebieg z punktem przegięcia. Prąd ładowania kondensatora, będący jednocześnie prądem cewki, narasta od wartości zerowej z zachowaniem ciągłości, a więc spełniając warunki nakładane przez prawa komutacji. W obwodzie RC widoczny jest gwałtowny skok prądu w chwili przełączenia (prawa komutacji nie dotyczą prądu kondensatora). | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd24.png]] | |||
|valign="top"|'''Przypadek aperiodyczny krytyczny''' | |||
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji <math>R=2\sqrt{\frac{L}{C}}</math> oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem | |||
: <math>I(t)=\frac{E/L}{(s+\frac{R}{2L})^2}</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd25.png]] | |||
|valign="top"|Zastosowanie wzoru na residuum dla pierwiastka podwójnego <math>s_1=s_2=-\frac{R}{2L}=-\alpha</math> prowadzi do następującej postaci prądu cewki <math>i(t)</math> | |||
: <math>i(t)=\frac{E}{L}e^{-\frac{R}{2L}t}</math> | |||
W analogiczny sposób można wyznaczyć pozostałe przebiegi (napięcia kondensatora i cewki) dla stanu aperiodycznego krytycznego. W przypadku napięcia na cewce bezpośrednio poprzez różniczkowanie funkcji czasowej prądu otrzymuje się | |||
: <math>u_L(t)=L\frac{di}{dt}=Ee^{-\frac{R}{2L}t}(1-\frac{R}{2L}t)</math> | |||
Napięcie na kondensatorze w stanie nieustalonym można uzyskać bezpośrednio z prawa napięciowego Kirchhoffa napisanego dla obwodu z rys. pierwszego na slajdzie 10 po przełączeniu. Mianowicie | |||
<math>u_C(t)=E-Ri_L(t)-u_L(t)=E-E^{-\frac{R}{2L}t}(1+\frac{R}{2L}t) </math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd26.png]] | |||
|valign="top"|Na slajdzie 26 przedstawiono przebieg ładowania kondensatora w stanie aperiodycznym krytycznym na tle przypadku aperiodycznego. | |||
Jedyna różnica występuje w czasie trwania stanu przejściowego, który najszybciej zanika dla przypadku krytycznego. Charakter przebiegu prądu i napięć w obwodzie dla przypadku aperiodycznego krytycznego jest podobny do zwykłego przypadku aperiodycznego, z tym, że najszybciej uzyskiwany jest stan ustalony (stan przejściowy trwa najkrócej z możliwych). | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd27.png]] | |||
|valign="top"|'''Przypadek oscylacyjny''' | |||
Jedyna różnica występuje w czasie trwania stanu przejściowego, który najszybciej zanika dla przypadku krytycznego. Charakter przebiegu prądu i napięć w obwodzie dla przypadku aperiodycznego krytycznego jest podobny do zwykłego przypadku aperiodycznego, z tym, że najszybciej uzyskiwany jest stan ustalony (stan przejściowy trwa najkrócej z możliwych). | |||
Przypadek oscylacyjny zmian prądu i napięć w obwodzie szeregowym RLC występuje przy spełnieniu warunku <math>R<2\sqrt{\frac{L}{C}}</math> a więc przy małych wartościach rezystancji R. W tym przypadku oba bieguny są zespolone. Dla wyznaczenia postaci czasowej prądu wygodniej jest zastosować metodę tablic transformat. W tym celu należy przekształcić wyrażenie na prąd operatorowy w taki sposób, aby doprowadzić je do postaci występującej w tablicy 12.1. | |||
Dla zadanej postaci prądu przekształcenia te są jak następuje | |||
|} | |||
Wersja z 02:50, 2 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
3) Stan przejściowy po przełączeniu
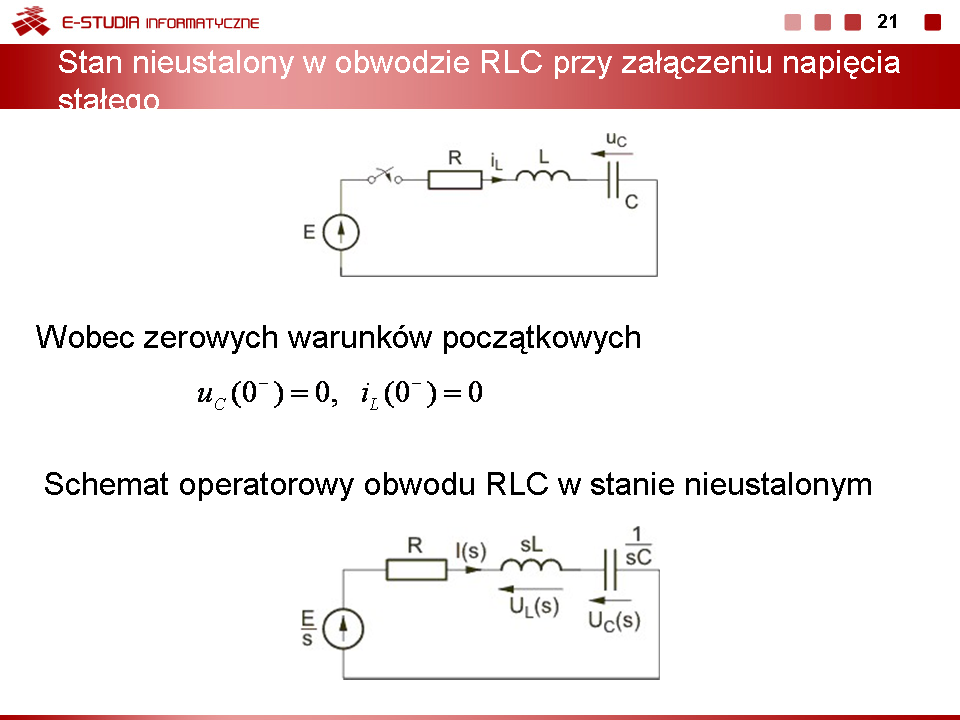
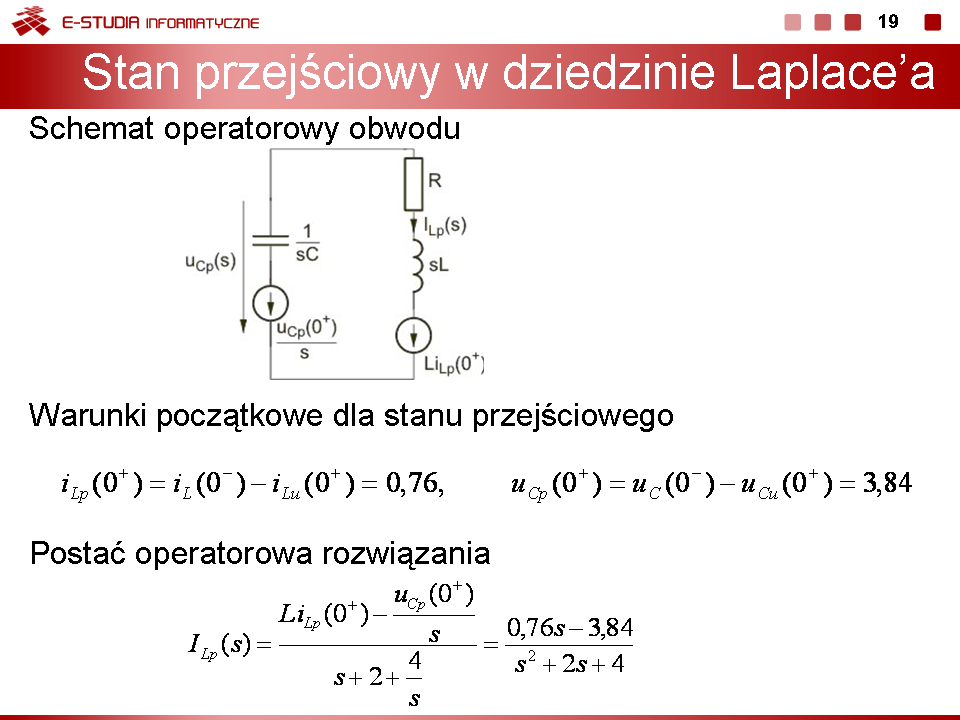
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|

|
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |