PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 392: | Linia 392: | ||
|valign="top"|''Przykład '' | |valign="top"|''Przykład '' | ||
Określić prąd cewki w stanie nieustalonym po przełączeniu w obwodzie przedstawionym na slajdzie 14. Przyjąć następujące wartości parametrów obwodu: <math>R=2\ | Określić prąd cewki w stanie nieustalonym po przełączeniu w obwodzie przedstawionym na slajdzie 14. Przyjąć następujące wartości parametrów obwodu: <math>R=2\Omega</math>, <math>L=1H\,</math>, <math>C=1/4F\,</math>. Zakładamy, że przełączanie zapewnia ciągłość prądu cewki podlegającej przełączeniu. | ||
| Linia 533: | Linia 533: | ||
Rozpatrzymy najpierw przypadek pierwszy (aperiodyczny). Ze względu na to, że oba bieguny są rzeczywiste w obliczeniach transformaty odwrotnej najwygodniej jest zastosować metodę residuów. Zgodnie z nią przebieg czasowy prądu <math>i(t)</math> można zapisać w postaci | Rozpatrzymy najpierw przypadek pierwszy (aperiodyczny). Ze względu na to, że oba bieguny są rzeczywiste w obliczeniach transformaty odwrotnej najwygodniej jest zastosować metodę residuów. Zgodnie z nią przebieg czasowy prądu <math>i(t)</math> można zapisać w postaci | ||
<math>i(t)=\frac{E}{2L\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}}\left[e^{s_1t}-e^{s_2t} \right]=</math> | |||
<math>=\frac{E}{L\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}}e^{-\frac{R}{2L}t}sh(\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}t)</math> | |||
We wzorze występuje czynnik tłumiący typu wykładniczego <math>e^{-\frac{R}{2L}t}</math>. Wielkość <math>\alpha=\frac{R}{2L}</math> nazywana jest współczynnikiem tłumienia. Jej wartość jest proporcjonalna do wartości rezystancji. Im większa rezystancja tym większe tłumienie w obwodzie. | |||
W podobny sposób wyznaczyć można pozostałe przebiegi czasowe w obwodzie: napięcie cewki i kondensatora. | |||
<math>u_C(t)=E+\frac{E}{2\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}}\left[s_2e^{s_1t}-s_1e^{s_2t} \right]</math> | |||
<math>u_L(t)=L\frac{di}{dt}=\frac{E}{2\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}}\left[s_1e^{s_1t}-s_2e^{s_2t} \right]</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd22.png]] | |||
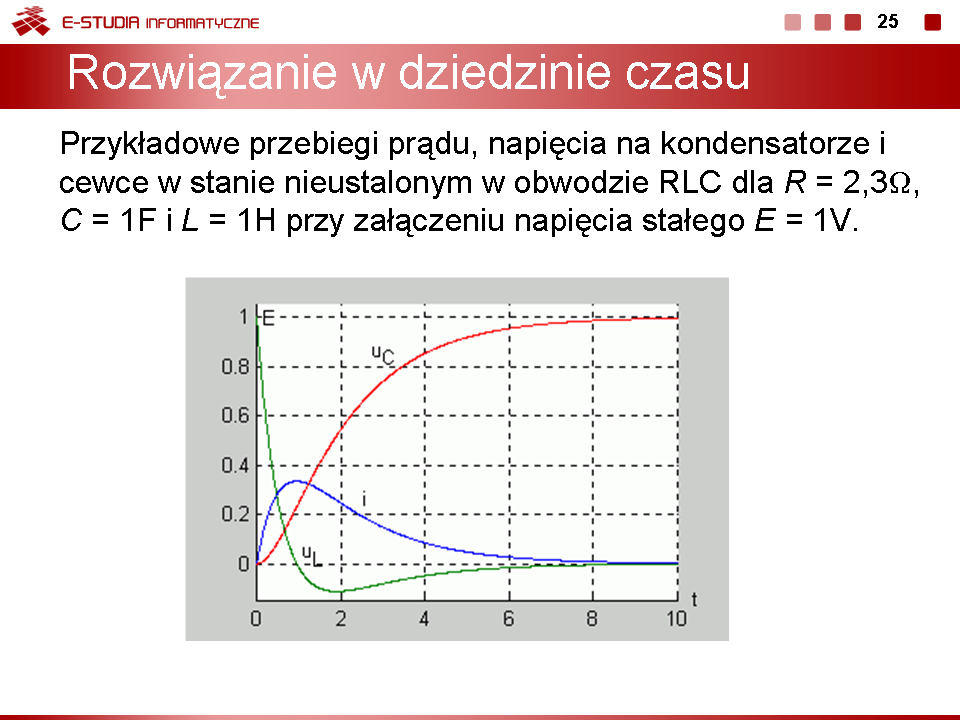
|valign="top"|Na rys. na slajdzie 22 przedstawiono przebiegi prądu, napięcia na kondensatorze i cewce w stanie nieustalonym w obwodzie RLC dla <math>R=2,3\Omega</math>, C = 1F i L = 1H przy załączeniu napięcia stałego E = 1V. Dla przyjętych wartości parametrów elementów mamy do czynienia z przypadkiem aperiodycznym. | |||
Wersja z 02:09, 2 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
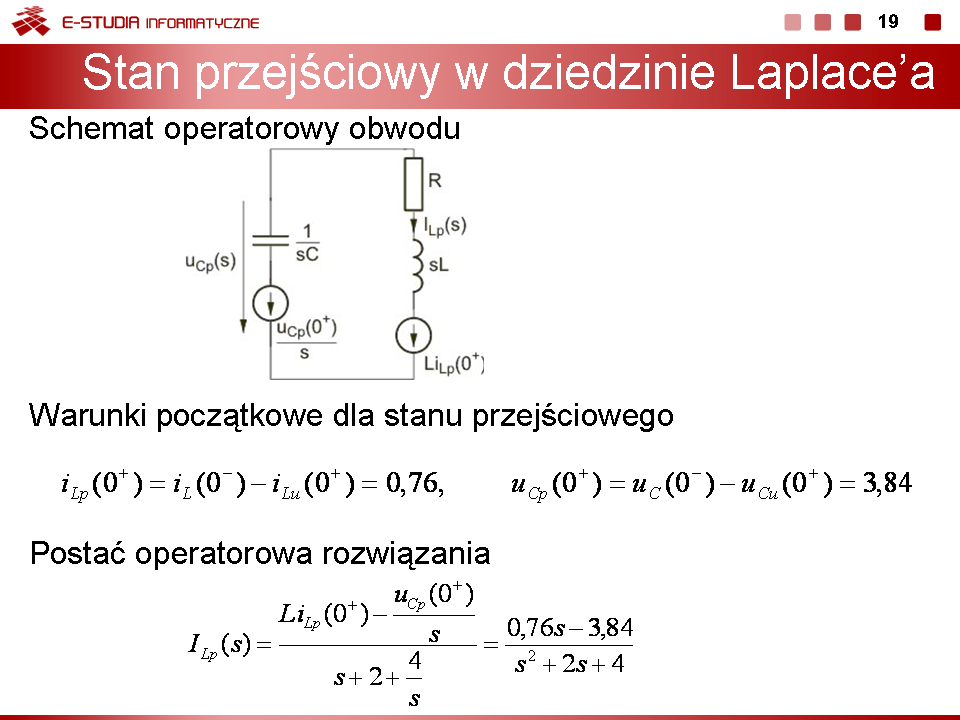
3) Stan przejściowy po przełączeniu
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|