Matematyka dyskretna 1/Ćwiczenia 13: Grafy II

Grafy II

Ćwiczenie 1

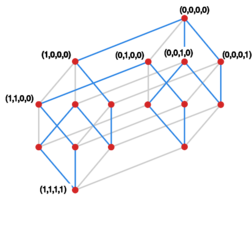
Kostka $k$ -wymiarowa ${{𝒬}}_k$ jest grafem, którego wierzchołki to ciągi $(a_1,a_2,\dots ,a_k)$ , gdzie $a_i=0,1$ , a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji. Oblicz liczbę wierzchołków, krawędzi oraz rozmiar najdłuższego cyklu.

Wskazówka

Aby znaleźć liczbę wierzchołków policz liczbę $k$ -elementowych ciągów złożonych z $0$ i $1$ . Przy znalezieniu liczby krawędzi przydatna będzie znajomość stopnia wierzchołków. Najdłuższy cykl, to cykl przechodzący przez wszystkie wierzchołki. Konstrukcję takiego cyklu przeprowadź indukcyjnie ze względu na $k$ .

Rozwiązanie

Cykl $16$ -elementowy w kostce ${{𝒬}}_4$

• Wierzchołki $\mathsf{V}\left({{𝒬}}_k\right)$ odpowiadają ciągom $(a_1,a_2,\dots ,a_k)$ , gdzie $a_i=0,1$. Liczba $k$ -elementowych ciągów liczb z dwuelementowego zbioru wynosi $2^k$ .
• Z kolei krawędzie łączą te ciągi, które różnią się na jednej tylko pozycji. Ciąg ze względu na konkretną pozycję jest sąsiedni z dokładnie jednym ciągiem. Stopień dowolnego wierzchołka równy jest więc $k$. Ponieważ każda krawędź ma dwa końce, to liczba wszystkich krawędzi jest równa $\frac{k\cdot 2^k}{2}=k\cdot 2^{k-1}$ .
• Najdłuższy cykl w ${{𝒬}}_k$ jest cyklem przechodzącym przez wszystkie wierzchołki. Wykażemy jego istnienie indukcyjnie ze względu na $k$ , pokazując ścieżkę z wierzchołka $(0,0,\dots ,0)$ do $(1,0,\dots ,0)$ , przechodzącą przez wszystkie wierzchołki.

Kostkę ${{𝒬}}_{k+1}$ można rozłożyć na dwie kostki w ten sposób, że w pierwszej znajdą się wszystkie wierzchołki odpowiadające ciągom zaczynającym się od $0$ , czyli $(0,a_2,\dots ,a_{k+1})$ , a w drugiej wierzchołki odpowiadające ciągom zaczynającym się od $1$ , czyli $(1,a_2,\dots ,a_{k+1})$ . Na mocy założenia indukcyjnego otrzymujemy ścieżkę z wierzchołka $(0,0,0,\dots ,0)$ do $(0,1,0,\dots ,0)$ , przechodzącą przez wszystkie wierzchołki pierwszej kostki. Analogicznie otrzymujemy także ścieżkę z wierzchołka $(1,0,0,\dots ,0)$ do $(1,1,0,\dots ,0)$ , przechodzącą przez wszystkie wierzchołki drugiej kostki. Po złożeniu obu ścieżek w ścieżkę postaci

$\begin{array}{rlr}(0,0,0,\dots ,0)\to \dots \to (0,1,0,\dots ,0)\to (1,1,0,\dots ,0)\to \dots & & \\ \dots \to (1,0,0,\dots ,0)& & \end{array}$

otrzymujemy szukaną ścieżkę. W konsekwencji otrzymujemy, że najdłuższa ścieżka ${{𝒬}}_k$ składa się ze wszystkich $2^k$ wierzchołków.

Ćwiczenie 2

Dla jakich wartości $n$ grafy ${{𝒦}}_n$ , ${{𝒦}}_{n,m}$ , ${{𝒬}}_n$ są eulerowskie.

Wskazówka

Skorzystaj z twierdzenia 13.1.

Rozwiązanie

Korzystając z twierdzenia 13.1 otrzymujemy warunek, że każdy graf eulerowski musi posiadać jedynie wierzchołki o stopniu parzystym.

• W klice ${{𝒦}}_n$ , każdy wierzchołek ma stopień równy $n-1$ , więc eulerowskimi są jedynie kliki ${{𝒦}}_{2k+1}$ o $2k+1$ wierzchołkach, gdzie $k=0,1,2,\dots$ .
• W pełnym grafie dwudzielnym ${{𝒦}}_{n,m}$ wierzchołki mają stopnie równe $n$ lub $m$ . Wsród pełnych grafów dwudzielnych eulerowskie są jedynie grafy ${{𝒦}}_{2k,2l}$ dla $k,l=0,1,2,\dots$ .
• W kostce ${{𝒬}}_n$ każdy wierzchołek ma $n$ sąsiadów, więc eulerowskie są kostki ${{𝒬}}_{2k}$ dla $k=0,1,2,\dots$ .

Ćwiczenie 3

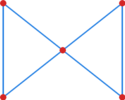
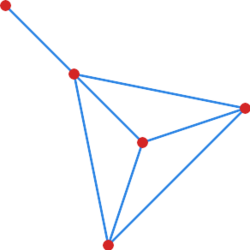
Przedstaw cztery pięciowierzchołkowe grafy -- kolejno graf który:

• nie jest hamiltonowski i nie jest eulerowski
• nie jest hamiltonowski, ale jest eulerowski
• jest hamiltonowski i nie jest eulerowski
• jest hamiltonowski i eulerowski.

Wskazówka

Skorzystaj z definicji grafu eulerowskiego i hamiltonowskiego.

Rozwiązanie

<flash>file=Cw grafy eul ham.swf|width=250|height=200</flash> <div.thumbcaption>Przykłady na: graf niehamiltonowski i nieeulerowski(a), graf niehamiltonowski ale eulerowskim (b), graf hamiltonowski lecz nieeulerowski (c),

oraz graf eulerowski będący zarazem hamiltonowskim (d)

Rozwiązanie jest przedstawione na rysunku.

Ćwiczenie 4

Dla jakich wartości $n$ grafy ${{𝒦}}_n$ , ${{𝒦}}_{n,m}$ , ${{𝒬}}_n$ są hamiltonowskie.

Wskazówka

Wyciągnij wnioski o liczności $V_1$ oraz $V_2$ z istnienia cyklu Hamiltona w grafie ${{𝒦}}_{n,m}=(V_1\cup V_2,E)$ . W odpowiedzi na pytanie, które kostki posiadają cykl Hamiltona, wróć do ćwiczenia 1.

Rozwiązanie

• Każda klika $n\ge 3$ elementowa jest hamiltonowska, ponieważ w klice dowolne dwa elementy są połączone krawędzią,

dowolny ciąg wszystkich elementów tworzy więc cykl.

• W pełnym grafie dwudzielnym $\mathbf{𝐆}=(V_1\cup V_2,E)$ dowolna ścieżka ma na przemian wierzchołki ze zbiorów $V_1$ oraz $V_2$, tzn. ścieżka ma postać

$v_1\to v_2\to v_3\to \dots v_k\to v_1,$

gdzie $v_1,v_3,v_5,\dots \in V_1$ , zaś $v_2,v_4,v_6,\dots \in V_2$ . Jeżeli skojarzymy wierzchołek $v_1$ z wierzchołkiem $v_2$ , wierzchołek $v_3$ z wierzchołkiem $v_4$ i w ogólności $v_{2j+1}$ z $v_{2j+2}$ , to wykorzystamy wszystkie wierzchołki grafu $\mathbf{𝐆}$ . Skonstruowane zostało skojarzenie wierzchołków z $V_1$ z wierzchołkami z $V_2$ wykorzystujące wszystkie wierzchołki, więc $\left|V_1\right|=\left|V_2\right|$ . Pełny graf dwudzielny ${{𝒦}}_{n,m}$ jest więc hamiltonowski wtedy i tylko wtedy, gdy $n=m$ .

• Ścieżka o maksymalnej długości znaleziona w ćwiczeniu 1 jest ścieżką Hamiltona. Otrzymujemy więc wniosek, że każda kostka jest grafem hamiltonowskim.

Graf Petersena

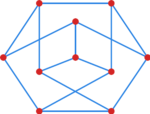
Ćwiczenie 5

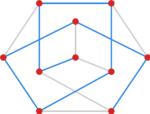
Czy graf Petersena (patrz rysunek) ma ścieżkę Hamiltona.

Rozwiązanie

Ścieżka Hamiltona w grafie Petersena

Ścieżka Hamiltona w grafie Petersena została przedstawiona na rysunku.

Ćwiczenie 6

Podaj przykład grafu ilustrujący, że warunek $\mathrm{deg}v\ge n/2$ występujący w Twierdzeniu Diraca 13.5 nie może być zastąpiony warunkiem $\mathrm{deg}v\ge n/2-1$ .

Wskazówka

Przeanalizuj dowód twierdzenia Ore'a (patrz tw. 13.4). W którym miejscu załamałby się ten dowód, gdyby istniały wierzchołki $v,w$ takie, że $\mathrm{deg}v+\mathrm{deg}w=n-1$ .

Rozwiązanie

Kontrprzykład do zmodyfikowanego twierdzenia Diraca

Jeżeli w wypowiedzi Twierdzenia Diraca, warunek $\mathrm{deg}v\ge n/2$ zastąpimy warunkiem $\mathrm{deg}v\ge n/2-1$ , to tak zmodyfikowane zdanie ma kontrprzykład przedstawiony na rysunku.

Ćwiczenie 7

Wykaż, że $n$ elementowy $\mathbf{𝐆}$ jest hamiltonowski jeśli tylko ma przynajmniej $(n-1)(n-2)/2+2$ krawędzi. Podaj przykład grafu niehamiltonowskiego z $n$ wierzchołkami i $(n-1)(n-2)/2+1$ krawędziami.

Wskazówka

Skorzystaj z Twierdzenia Ore'a (patrz tw. 13.4).

Rozwiązanie

Graf o $5$ wierzchołkach i $7$ krawędziach, ale bez cyklu Hamiltona

Niech $u$ i $v$ będą niesąsiednimi wierzchołkami grafu $\mathbf{𝐆}$ . Dopełnienie grafu $\mathbf{𝐆}$ posiada co najwyżej

$\frac{n(n-1)}{2}-(\frac{(n-1)(n-2)}{2}-2)=n-3$

krawędzi, więc $u$ i $v$ mogą być incydentne w sumie z co najwyżej $n-3$ krawędziami w $\overline{\mathbf{𝐆}}$ . Liczba krawędzi incydentnych z $u$ lub $v$ w grafie pełnym $(\mathsf{V}\left(\mathbf{𝐆}\right),{{𝒫}}_2\left(\mathsf{V}\left(\mathbf{𝐆}\right)\right))$ , jest równa $2n-3$ . Dopełnienie grafu $\mathbf{𝐆}$ jest to graf postaci $\overline{\mathbf{𝐆}}=(\mathsf{V}\left(\mathbf{𝐆}\right),{{𝒫}}_2\left(\mathsf{V}\left(\mathbf{𝐆}\right)\right)-\mathsf{E}\left(\mathbf{𝐆}\right))$ , więc liczba krawędzi incydentnych z $u$ lub $v$ to co najmniej

$(2n-3)-(n-3)=n$

Wierzchołki $u$ i $v$ nie sąsiadują ze sobą, więc zbiory incydentnych krawędzi są rozłączne, co w konsekwencji daje że

$\mathsf{d}\mathsf{e}\mathsf{g}u+\mathsf{d}\mathsf{e}\mathsf{g}v\ge n$

Na mocy więc Twierdzenia Ore'a (patrz tw. 13.4) otrzymujemy, że $\mathbf{𝐆}$ jest hamiltonowski.

Wartość $(n-1)(n-2)/2+2$ jest najmniejszą taką liczbą, że każdy graf o $n$ wierzchołkach i co najmniej tylu krawędziach jest hamiltonowski. Graf o $n=5$ wierzchołkach i $(n-1)(n-2)/2+1=7$ krawędziach, który nie jest hamiltonowski jest przedstawiony na rysunku 6.

Ćwiczenie 8

Wykaż, że każde drzewo jest grafem dwudzielnym. Które drzewa są pełnymi grafami dwudzielnymi?

Wskazówka

Dla drzewa $T=(V,E)$ wybierz dowolny wierzchołek $v\in V$ i zdefiniuj odpowiedni podział $V=V_1\cup V_2$ korzystając z parzystości odległości od $v$ . Kiedy pełny graf dwudzielny nie ma cykli?

Rozwiązanie

Niech $T=(V,E)$ będzie drzewem a $v\in V$ dowolnie wybranym jego wierzchołkiem. Podzielimy zbiór $V$ na wierzchołki, które:

• są oddalone od $v$ o odległość będącą liczbą parzystą - wraz z $v$ będą tworzyć zbiór $V_1$ ,
• są oddalone od $v$ o odległość będącą liczbą nieparzystą - te z kolei będą składać się na zbiór $V_2$ .

W drzewie pomiędzy dowolnymi wierzchołkami istnieje dokładnie jedna ścieżka, tak więc ścieżka świadcząca o odległości wierzchołka $w$ od wierzchołka $v$ jest jedyną ścieżką pomiędzy $v$ a $w$ . Niech $ux\in E$ dla wierzchołków $u,x\in V_i$. Ścieżka

$v\to \dots \to u\to x,$

ma długość innej parzystości niż ścieżka

$v\to \dots \to u,$

co przeczy temu, że $u$ oraz $v$ są razem w jednym zbiorze $V_i$ .

Drzewo jest pełnym grafem dwudzielnym wtedy i tylko wtedy gdy jest gwiazdą. Istotnie, gwiazda o $n$ liściach jest pełnym grafem dwudzielnym ${{𝒦}}_{1,n}$ . Z drugiej strony załóżmy, że drzewo $\mathbf{𝐓}=(V_1\cup V_2,E)$ jest pełnym grafem dwudzielnym, ale nie jest gwiazdą, czyli zawiera ścieżkę o długości $3$ , np.:

$u\to v\to w\to x$

Bez straty ogólności załóżmy, że $u\in V_1$ , tak więc $v,x\in V_2$ oraz $w\in V_1$ . W pełnym grafie dwudzielnym istnieje więc krawędź łącząca wierzchołek $x\in V_2$ z wierzchołkiem $u\in V_1$ . Mam więc cykl postaci:

$u\to v\to w\to x\to u,$

co przeczy temu, że $\mathbf{𝐓}$ jest drzewem.

Ćwiczenie 9

Udowodnij wierzchołkową wersję Twierdzenia Mengera.

Wskazówka

Naśladuj dowód Twierdzenia 13.8.

Rozwiązanie

Niech $w$ , $u$ będą dwoma różnymi i niesąsiednimi wierzchołkami spójnego grafu $\mathbf{𝐆}=(V,E)$ . Przez $k$ oznaczmy najmniejszą możliwą liczność zbioru wierzchołków rozdzielających $w$ , $u$ . Oczywiście każda droga łącząca $w$ z $u$ musi przejść przez każdy zbiór rozdzielający. A zatem dróg wierzchołkowo rozłącznych łączących $w$ z $u$ nie może być więcej niż $k$ . Tak więc wystarczy pokazać, że istnieje $k$ rozłącznych wierzchołkowo dróg z $w$ do $u$ .

Dowód przeprowadzimy indukcyjnie ze względu na liczbę wierzchołków w grafie $\mathbf{𝐆}$ rozważając dwa przypadki.

1. Pewien zbiór rozdzielający $X$ mocy $k$ ma wierzchołek niesąsiedni z $w$ oraz ma wierzchołek (być może inny) niesąsiedni z $u$ .

Graf $\mathbf{𝐆}$ , po usunięciu wszystkich wierzchołków z $X$ , podzieli się na dwie spójne składowe $W$ oraz $U$ , do których należą odpowiednio $w$ i $u$ .

Przez $W^{\prime }$ oznaczmy graf powstały z grafu $\mathbf{𝐆}$ poprzez ściągnięcie $U$ w jeden wierzchołek $u^{\prime }$ . Wtedy $u^{\prime }$ jest połączony z tymi wierzchołkami $t\in X$ , z którymi połączony był jakiś wierzchołek $s\in U$ . Krawędzie łączące wierzchołki wewnątrz $W$ pozostały niezmienione. Graf $U^{\prime }$ definiujemy analogicznie, poprzez ściągnięcie zbioru $W$ do wierzchołka $w^{\prime }$ .

W grafie $W^{\prime }$ minimalny zbiór rozdzielający wierzchołki $w,u^{\prime }$ posiada $k$ wierzchołków. Ponieważ założyliśmy, ze w $X$ istnieje wierzchołek niesąsiedni z $u$ , to $U$ ma co najmniej dwa wierzchołki, a zatem graf $W^{\prime }$ ma mniej wierzchołków niż $\mathbf{𝐆}$ . Tak wiec możemy skorzystać z założenia indukcyjnego otrzymując $k$ rozłącznych wierzchołkowo dróg łączących $w$ z $u^{\prime }$ w $W^{\prime }$ . Analogicznie w grafie $U$ otrzymujemy $k$ rozłącznych wierzchołkowo dróg łączących $w^{\prime }$ z $u$ . Sklejając odpowiednio drogi z obu tych rodzin otrzymujemy $k$ rozłącznych ścieżek łączących $w$ z $u$ w grafie $\mathbf{𝐆}$ .

2. W każdym zbiorze rozdzielającym $X$ o mocy $k$ , każdy wierzchołek jest sąsiedni do $w$ lub do $u$ .

Możemy wtedy założyć, że $\mathbf{𝐆}$ poza $w,u$ zawiera jedynie wierzchołki należące do któregoś zbioru rozdzielającego $w,u$ o liczności $k$ . Gdyby tak nie było i istniałby jakiś inny wierzchołek $v$ , to moglibyśmy $v$ usunąć i, na mocy założenia indukcyjnego, otrzymać natychmiast $k$ rozłącznych dróg łączących $w,u$ . Tak wiec pozostały nam jedynie te wierzchołki, które są w minimalnych zbiorach rozdzielających $w,u$ . To zaś, zgodnie z założeniem przypadku 2 oznacza, że każdy wierzchołek jest sąsiedni z $w$ lub z $u$ . W ten sposób drugi przypadek sprowadziliśmy do sytuacji, w której każda ścieżka z $w$ do $u$ ma co najwyżej dwie krawędzie. Wśród takich ścieżek nietrudno jest już wskazać $k$ rozłącznych wierzchołkowo.

Ćwiczenie 10

Korzystając z Twierdzenia Mengera udowodnij Twierdzenie Halla o skojarzeniach w grafach dwudzielnych.

Rozwiązanie

Dla grafu dwudzielnego $\mathbf{𝐆}=(V_1\cup V_2,E)$ , oraz funkcji $\mathrm{\Phi }\left(A\right)$ , która zwraca zbiór wierzchołków z $V_2$ sąsiednich z przynajmniej jednym wierzchołkiem w $A\subseteq V_1$ twierdzenie Hall'a (patrz tw. 13.7) mówi, że:

Pełne skojarzenie $V_1$ z $V_2$ istnieje wtedy i tylko wtedy, gdy $\left|A\right|\le \left|\mathrm{\Phi }\left(A\right)\right|$ , dla każdego podzbioru $A$ zbioru $V_1$ .

$\Rightarrow$ Implikacja ta wynika natychmiast z faktu, że jeśli w pełnym skojarzeniu $V_1$ z $V_2$ , w $\mathrm{\Phi }\left(A\right)$ jest $\left|A\right|$ wierzchołków skojarzonych z wierzchołkami z $A$ , co w szczególności implikuje, że $\left|A\right|\le \left|\mathrm{\Phi }\left(A\right)\right|$ .

$\Leftarrow$ Do grafu dwudzielnego $\mathbf{𝐆}=(V_1\cup V_2,E)$ dołóżmy dwa wierzchołki $v_1$ oraz $v_2$ łącząc $v_1$ ze wszystkimi wierzchołkami z $V_1$ , a $v_2$ ze wszystkimi wierzchołkami z $V_2$ . Rozważmy dowolny zbiór $S\subseteq V_1\cup V_2$ o $\left|V_1\right|-1$ wierzchołkach. Na mocy założenia otrzymujemy, że zbiór wierzchołków z $V_2$ sąsiadujących z wierzchołkami $V_1-S$ jest co najmniej tak duży, jak $V_1-S$ , czyli

$|V_1-S|\le \left|\mathrm{\Phi }(V_1-S)\right|$

Ponieważ $\left|S\right|<\left|V_1\right|$ , to $|V_2\cap S|<|V_1-S|\le \left|\mathrm{\Phi }(V_1-S)\right|$ , a zatem $\mathrm{\Phi }(V_1-S)-S\ne \mathrm{\varnothing }$ , czyli $\mathrm{\Phi }(V_1-S)\subseteq ̸S$ . Istnieją więc sąsiednie wierzchołki $u_1\in V_1-S$ oraz $u_2\in \mathrm{\Phi }(V_1-S)-S$ . Teraz, ścieżka postaci

$v_1\to u_1\to u_2\to v_2$

świadczy więc o tym, że $S$ nie był w stanie rozdzielić wierzchołka $v_1$ od $v_2$ . Na mocy wierzchołkowej wersji twierdzenia Mangera (patrz ćw. 9), istnieje $\left|V_1\right|$ rozłącznych wierzchołkowo ścieżek łączących $v_1$ z $v_2$ . Każda taka ścieżka musi być postaci

$v_1\to w_1\to w_2\to v_2,$

gdzie $w_1\in V_1$ oraz $w_2\in V_2$ . Istotnie ścieżek tych jest dokładnie $\left|V_1\right|$ , więc każda z nich przechodzi dokładnie raz przez $V_1$ i dokładnie raz przez $V_2$ . Usuwając teraz z każdej takiej ścieżki wierzchołki $v_1,v_2$ , otrzymujemy pełne skojarzenie $V_1$ z $V_2$ .