PEE Moduł 6: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 254: | Linia 254: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd17.png]] | ||
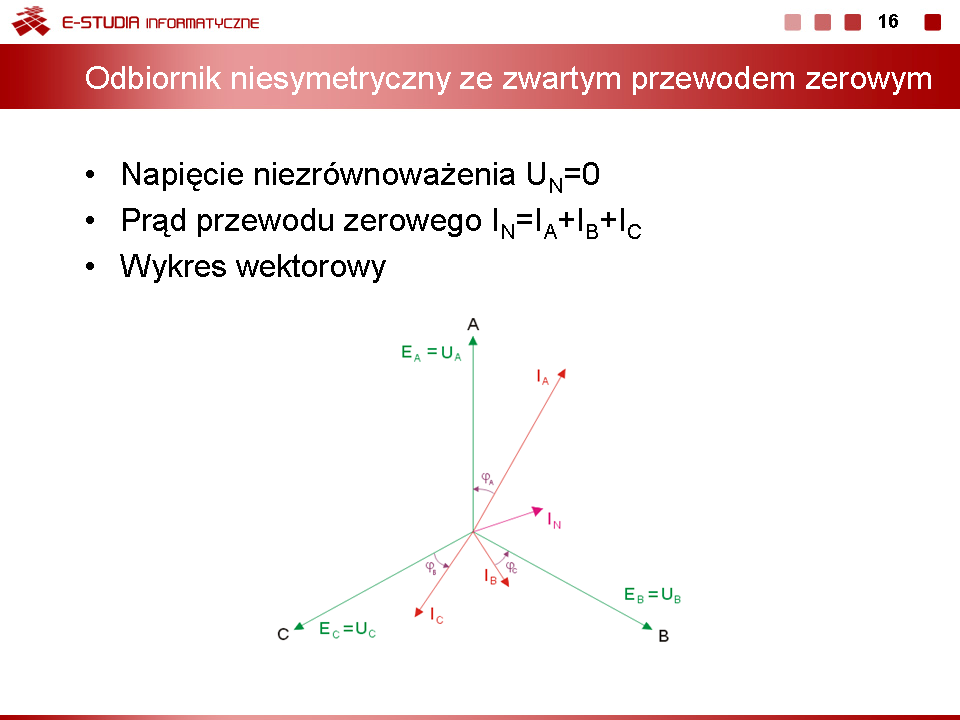
|valign="top"| | |valign="top"|''Przykład'' | ||
Obliczyć prądy i napięcia poszczególnych faz odbiornika w układzie przedstawionym na rysunku obok (slajd 17). Przyjąć zasilanie trójfazowe symetryczne o napięciu fazowym równym <math>400V</math>. Wartości parametrów obwodu są następujące: <math>R=40\Omega</math>, <math>X_C=30\Omega</math>, <math>X_L=60\Omega</math>, <math>X_{12}=10\Omega</math>, <math>X_{23}=20\Omega</math>, <math>X_{31}=20\Omega</math>. | |||
|} | |} | ||
| Linia 261: | Linia 264: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd18.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd18.png]] | ||
|valign="top"| | |valign="top"|''Rozwiązanie'' | ||
Ze względu na występowanie sprzężenia magnetycznego pierwszym etapem rozwiązania jest eliminacja tych sprzężeń. Układ odbiornika po likwidacji sprzężeń magnetycznych jest przedstawiony na rysunku obok (slajd 18). | |||
|} | |} | ||
| Linia 268: | Linia 273: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd19.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd19.png]] | ||
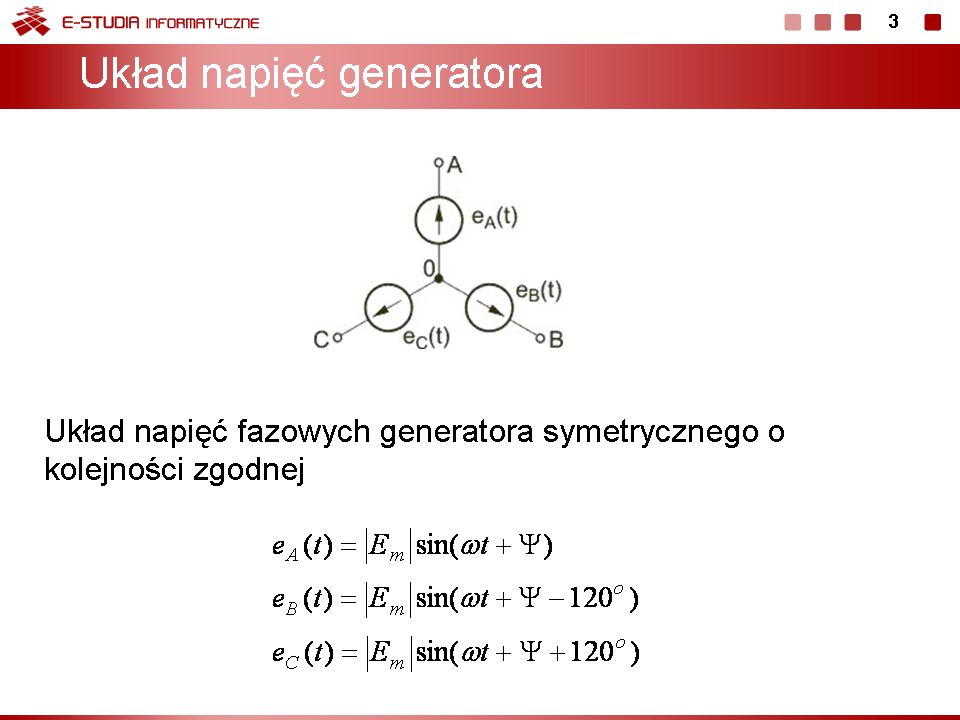
|valign="top"| | |valign="top"|Przyjmijmy układ napięć fazowych generatora w następującej postaci | ||
: <math>E_A=400e^{j0}</math> | |||
: <math>E_B=400e^{-j120}</math> | |||
: <math>E_C=400e^{j120}</math> | |||
Impedancje poszczególnych faz odbiornika z rysunku na slajdzie 18 są równe | |||
: <math>Z_A=40+j40=40\sqrt{2}e^{j45^\circ}</math> | |||
: <math>Z_B=j60=60e^{j90^\circ}</math> | |||
: <math>Z_C=0</math> | |||
|} | |} | ||
| Linia 275: | Linia 291: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd20.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd20.png]] | ||
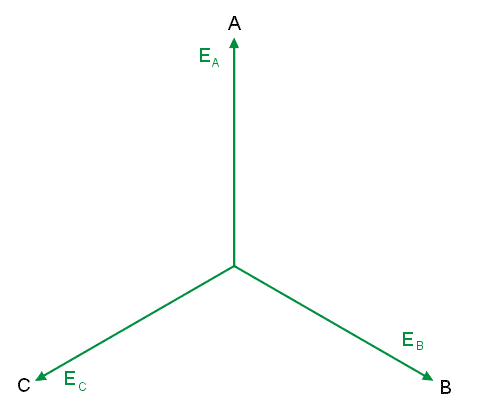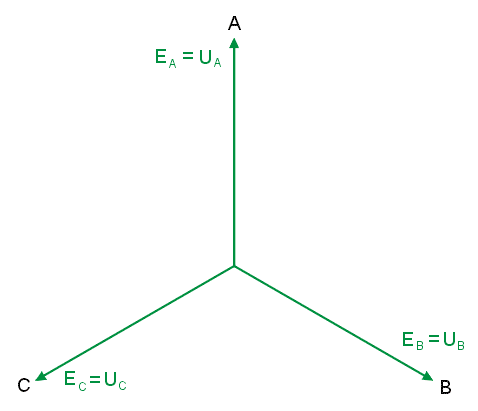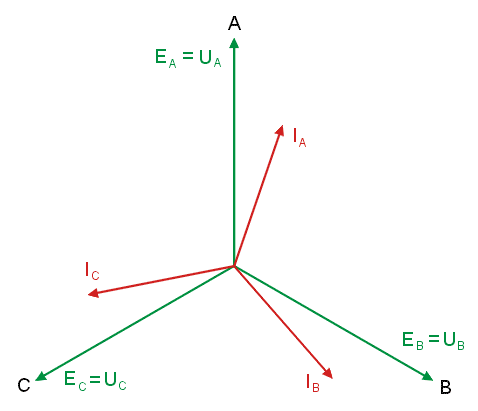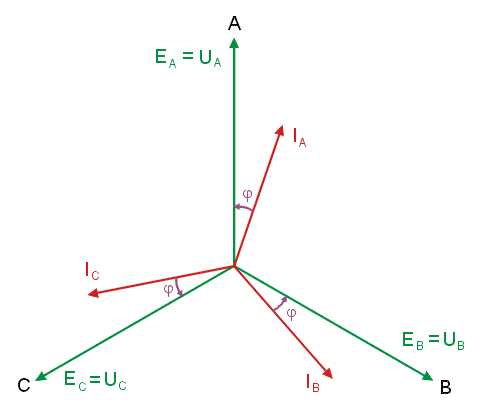
|valign="top"| | |valign="top"|Wobec zwarcia w fazie C odbiornika (<math>Z_C = 0</math>) nie zachodzi potrzeba stosowania wzoru | ||
: <math>U_N={E_AY_A+E_BY_B+E_CY_C \over (Y_A+Y_B+Y_C+Y_N)}</math> | |||
do wyznaczenia napięcia niezrównoważenia, gdyż <math>U_N = E_C</math>. W tej sytuacji poszczególne prądy fazowe są równe | |||
: <math>I_A={E_A-U_N \over Z_A}={400-400e^{j120^\circ} \over 40\sqrt{2}e^{j45^\circ}}=5\sqrt{2}e^{-j75^\circ}=1,8-j6,8</math> | |||
: <math>I_B={E_B-U_N \over Z_B}={400e^{-j120^\circ}-400e^{j120^\circ} \over 60e^{j90^\circ}}=-11,6</math> | |||
: <math>I_C=-I_A-I_B=9,8+j6,8</math> | |||
Po obliczeniu prądów na podstawie schematu zastępczego bez sprzężeń magnetycznych dla wyznaczenia napięć w układzie należy powrócić do obwodu ze sprzężeniami. Rzeczywiste napięcia na fazach odbiornika wynoszą | |||
: <math>U_A=RI_A+jX_LI_A+jX_{12}I_B+jX_{31}I_C=322+j263</math> | |||
: <math>U_B=jX_LI_B+jX_{12}I_A+jX_{23}I_C=-18-j335</math> | |||
: <math>U_C=jX_LI_C+jX_{31}I_A+jX_{23}I_B-jX_CI_C=-18</math> | |||
Zauważmy, że istnieje ogromna różnica między rzeczywistym napięciem <math>U_C</math> w fazie C, <math>U_C=-18</math>, a napięciem w tej samej fazie w obwodzie po likwidacji sprzężeń, <math>U_C=0</math>. Obwód po likwidacji sprzężeń jest równoważny obwodowi oryginalnemu jedynie pod względem prądowym. Napięcia na gałęziach zawierających cewki sprzężone nie odpowiadają ich odpowiednikom w obwodzie bez sprzężeń. | |||
|} | |} | ||
Wersja z 11:04, 1 sie 2006

|
Wykład 6. Układy trójfazowe |

|
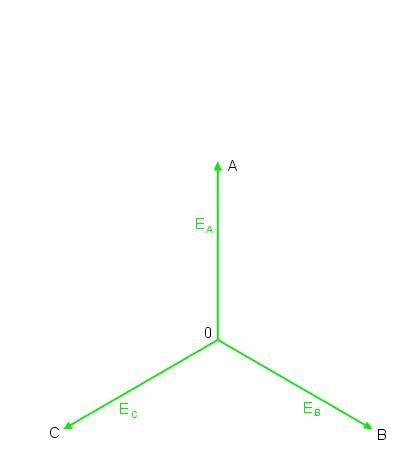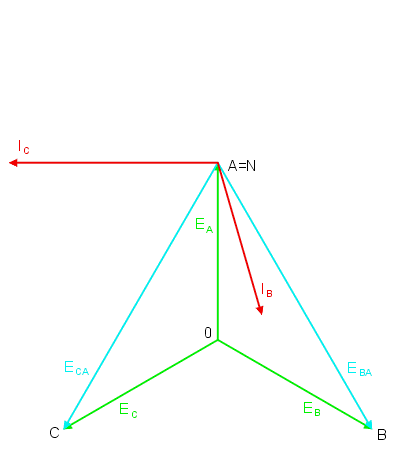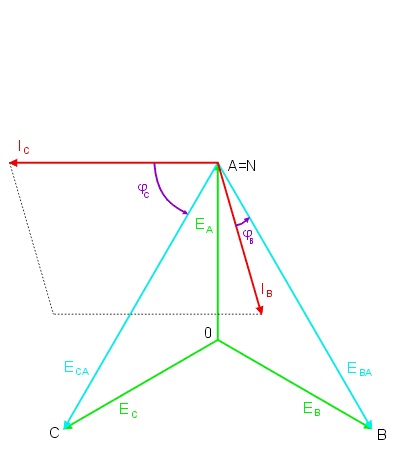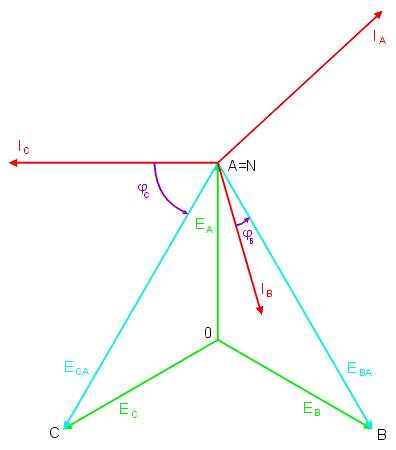
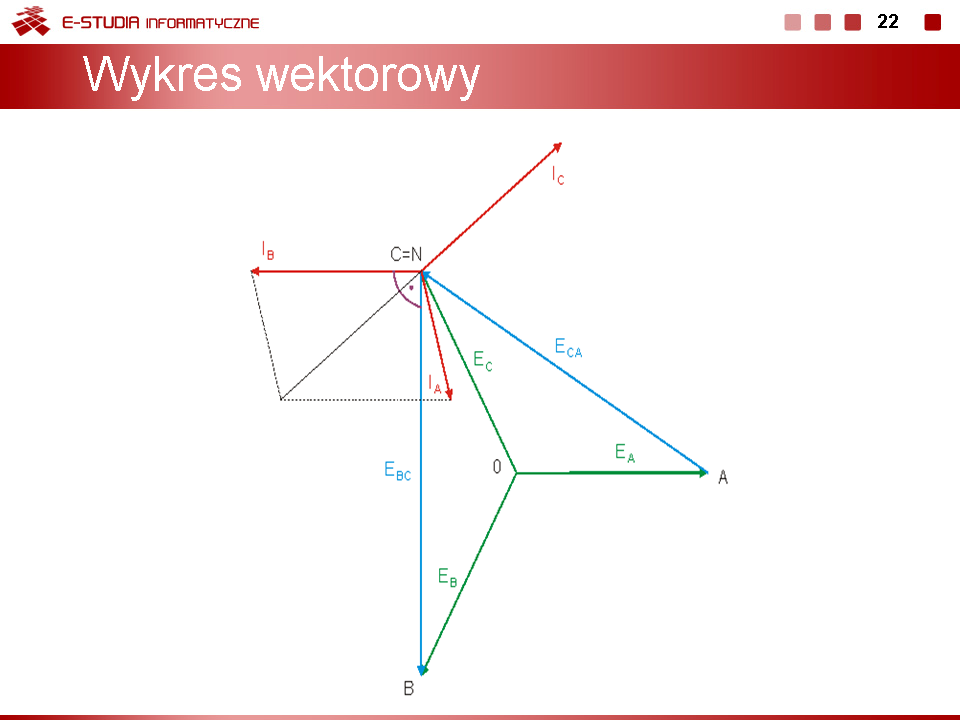
W pracy układu trójfazowego gwiazdowego można wyróżnić kilka szczególnych przypadków.
|

|
Przyjmijmy układ napięć fazowych generatora w następującej postaci
Impedancje poszczególnych faz odbiornika z rysunku na slajdzie 18 są równe |
|

|

|