Języki, automaty i obliczenia/Ćwiczenia 7: Twierdzenie Kleene'ego. Własności języków i gramatyk regularnych: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „.</math>” na „</math>.” |
m Zastępowanie tekstu – „,</math>” na „</math>,” |
||
| Linia 6: | Linia 6: | ||
(S_{\mathcal C},A,f_{\mathcal C},s_{\mathcal C},F_{\mathcal C})</math></center> | (S_{\mathcal C},A,f_{\mathcal C},s_{\mathcal C},F_{\mathcal C})</math></center> | ||
<center><math>S_{\mathcal B} = \{s_{\mathcal B},s_1,s_2\}, | <center><math>S_{\mathcal B} = \{s_{\mathcal B},s_1,s_2\}, | ||
\;\;F_{\mathcal B} = \{s_2\},\;\;\; S_{\mathcal C} = \{s_{\mathcal C},s\},\;\; F_{\mathcal C} = \{s\} | \;\;F_{\mathcal B} = \{s_2\},\;\;\; S_{\mathcal C} = \{s_{\mathcal C},s\},\;\; F_{\mathcal C} = \{s\}</math>,</center> | ||
gdzie | gdzie | ||
| Linia 14: | Linia 14: | ||
\hline b & s_{\mathcal C} & s_{\mathcal C} \\ \hline \end{array} </math></center> | \hline b & s_{\mathcal C} & s_{\mathcal C} \\ \hline \end{array} </math></center> | ||
skonstruuj automat <math>\mathcal A</math> taki, że <center><math>L({\mathcal A}) = L({\mathcal B}) \cap L({\mathcal C}) | skonstruuj automat <math>\mathcal A</math> taki, że <center><math>L({\mathcal A}) = L({\mathcal B}) \cap L({\mathcal C})</math>,</center> | ||
}} | }} | ||
| Linia 30: | Linia 30: | ||
Niech <math>A = \{a,b\}</math>. Dla automatu <center><math>{\mathcal B} = (S_{\mathcal | Niech <math>A = \{a,b\}</math>. Dla automatu <center><math>{\mathcal B} = (S_{\mathcal | ||
B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B}) | B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B})</math>,</center> | ||
gdzie | gdzie | ||
<center><math>S_{\mathcal B} = \{s_{\mathcal B},s_1,s_2\}, | <center><math>S_{\mathcal B} = \{s_{\mathcal B},s_1,s_2\}, | ||
\;\;F_{\mathcal B} = \{s_1\} | \;\;F_{\mathcal B} = \{s_1\}</math>,</center> | ||
a funkcja przejść zdefiniowana jest | a funkcja przejść zdefiniowana jest | ||
następująco: | następująco: | ||
| Linia 150: | Linia 150: | ||
Niech <math>A = \{a,b\}</math>. Skonstruuj automat <math>\mathcal A</math>, taki że | Niech <math>A = \{a,b\}</math>. Skonstruuj automat <math>\mathcal A</math>, taki że | ||
1. <math>L({\mathcal A}) = L({\mathcal B}) \cup L({\mathcal C}) | 1. <math>L({\mathcal A}) = L({\mathcal B}) \cup L({\mathcal C})</math>, gdzie <center><math>{\mathcal B} = | ||
(S_{\mathcal B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B}),\;\;\;\; {\mathcal C} = | (S_{\mathcal B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B}),\;\;\;\; {\mathcal C} = | ||
(S_{\mathcal C},A,f_{\mathcal C},s_{\mathcal C},F_{\mathcal C}) | (S_{\mathcal C},A,f_{\mathcal C},s_{\mathcal C},F_{\mathcal C})</math>,</center> | ||
<center><math>S_{\mathcal B} = | <center><math>S_{\mathcal B} = | ||
\{s_{\mathcal B},s_1,s_2\}, \;\;F_{\mathcal B} = \{s_2\},\;\;\; S_{\mathcal C} = | \{s_{\mathcal B},s_1,s_2\}, \;\;F_{\mathcal B} = \{s_2\},\;\;\; S_{\mathcal C} = | ||
\{s_{\mathcal C},{s'}_1,{s'}_2\},\;\; F_{\mathcal C} = \{{s'}_2\} | \{s_{\mathcal C},{s'}_1,{s'}_2\},\;\; F_{\mathcal C} = \{{s'}_2\}</math>,</center> | ||
| Linia 162: | Linia 162: | ||
\begin{array} {c|c|c|c|} f_{\mathcal C} &s_{\mathcal C} &{s'}_1&{s'}_2 \\ \hline a & {s'}_1 & {s'}_1& {s'}_2 \\ | \begin{array} {c|c|c|c|} f_{\mathcal C} &s_{\mathcal C} &{s'}_1&{s'}_2 \\ \hline a & {s'}_1 & {s'}_1& {s'}_2 \\ | ||
\hline b & {s'}_2 & {s'}_1& {s'}_2 \\ \hline \end{array} </math></center> | \hline b & {s'}_2 & {s'}_1& {s'}_2 \\ \hline \end{array} </math></center> | ||
2. <math>L({\mathcal A}) = L({\mathcal B})^* | 2. <math>L({\mathcal A}) = L({\mathcal B})^*</math>, gdzie <center><math>{\mathcal B} = | ||
(S_{\mathcal B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B}) | (S_{\mathcal B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B})</math>,</center> | ||
<center><math>S_{\mathcal B} = \{s_{\mathcal B},s_1,s_2,s_3\}, \;\;F_{\mathcal | <center><math>S_{\mathcal B} = \{s_{\mathcal B},s_1,s_2,s_3\}, \;\;F_{\mathcal | ||
B} = \{s_2\} | B} = \{s_2\}</math>,</center> | ||
Wersja z 09:28, 5 wrz 2023
Ćwiczenia 7
Ćwiczenie 1
gdzie
Ćwiczenie 2
gdzie
a funkcja przejść zdefiniowana jest następująco:
skonstruuj automat deterministyczny taki, że
Ćwiczenie 3
Dane są dwa automaty nad tym samym alfabetem
i . Udowodnij,
że istnieje liczba taka, że jeśli dla każdego słowa o długości spełniona jest implikacja
,
to
Ćwiczenie 4
Niech będzie dowolnym alfabetem, a językiem regularnym. Udowodnij, że język jest też językiem regularnym.
Ćwiczenie 5
Udowodnij, że następujące języki nie są regularne:
- ,
- .
Ćwiczenie 6
Niech . Skonstruuj automat , taki że
1. , gdzie
Podaj dwie konstrukcje:
- opartą na dowodzie twierdzenia Kleene'ego,
- z wykorzystaniem automatu z pustymi przejściami.
Ćwiczenie 7
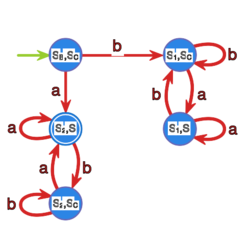
Skonstruuj minimalny automat , taki że , gdzie opisany jest
poniższym grafem: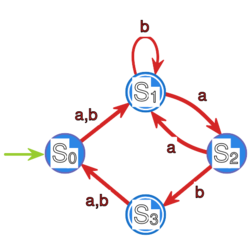
Ćwiczenie 8
Udowodnij, że następujące języki nie są regularne:
- ,
- .
Ćwiczenie 9
Zbuduj automat akceptujący język będący ogółem skończonych sekwencji binarnych, w których liczba zer jest podzielna przez dwa, a liczba jedynek przez 3, a następnie gramatykę generującą ten język.