PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 303: | Linia 303: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd19.png]] | ||
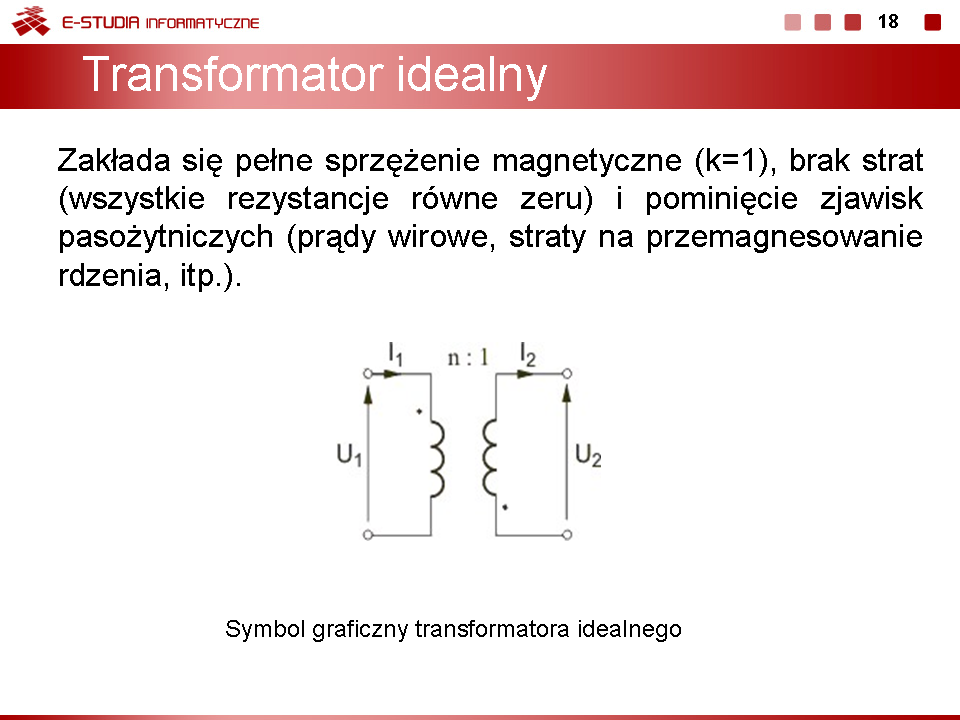
|valign="top"|Transformator idealny jest w pełni opisany poprzez tak zwaną '''przekładnię zwojową''', określającą stosunek napięcia pierwotnego do wtórnego ('''przekładnię napięciową''') na podstawie liczby zwojów pierwotnych i wtórnych. Przekładnia napięciowa transformatora idealnego niezależnie od sposobu wykonania i od obciążenia, powinna być równa przekładni zwojowej określonej wzorem | |valign="top"|Transformator idealny jest w pełni opisany poprzez tak zwaną '''przekładnię zwojową''', określającą stosunek napięcia pierwotnego do wtórnego ('''przekładnię napięciową''') na podstawie liczby zwojów pierwotnych i wtórnych. Przekładnia napięciowa transformatora idealnego niezależnie od sposobu wykonania i od obciążenia, powinna być równa przekładni zwojowej określonej wzorem | ||
| Linia 325: | Linia 325: | ||
<math>\begin{bmatrix}U_1\\I_1\end{bmatrix}=\begin{bmatrix}n&0 \\0&\frac{1}{n}\end{bmatrix}\begin{bmatrix}U_2\\I_2\end{bmatrix}</math> | <math>\begin{bmatrix}U_1\\I_1\end{bmatrix}=\begin{bmatrix}n&0 \\0&\frac{1}{n}\end{bmatrix}\begin{bmatrix}U_2\\I_2\end{bmatrix}</math> | ||
Powyższe równanie macierzowe nazywane jest równaniem łańcuchowym transformatora idealnego. Wykonanie transformatora idealnego w praktyce nie jest możliwe, jednak współczesne realizacje techniczne transformatorów zwłaszcza transformatory z rdzeniem ferromagnetycznym są bliskie ideału. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd20.png]] | |||
|valign="top"|'''Realizacja transformatora w układzie cewek magnetycznie sprzężonych''' | |||
Transformator rzeczywisty realizuje się w układzie cewek magnetycznie sprzężonych, nawiniętych na korpusie wykonanym zwykle z materiału ferromagnetycznego, zapewniającego bliskie idealnemu sprzężenie magnetyczne (k≈1). Model idealnego transformatora magnetycznego (bez uwzględnienia rezystancji uzwojeń) obciążonego impedancją <math>Z_o\,</math> jest przedstawiony na rysunku. | |||
Indukcyjności własne uzwojeń oznaczone są przez <math>L_1 i L_2</math> a indukcyjność wzajemna przez <math>M\,</math>, przy czym <math>M=k\sqrt{L_1L_2}</math> Napięcie zasilające wywołuje w obwodzie pierwotnym prąd <math>I_1\,</math>, wytwarzający strumień magnetyczny. Energia obwodu pierwotnego przenosi się do obwodu wtórnego poprzez sprzężenie magnetyczne, zaznaczone symbolicznie jako indukcyjność wzajemna <math>M\,</math>. Pod wpływem zaindukowanego napięcia przy zamkniętym obwodzie wtórnym płynie prąd <math>I_2\,</math>, odkładając na impedancji odbiornika napięcie <math>U_2\,</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd21.png]] | |||
|valign="top"|Analizując transformator w stanie ustalonym przy wymuszeniu sinusoidalnym zastosujemy metodę symboliczną. Z definicji sprzężenia magnetycznego obu cewek przy założonym zwrocie prądów i przyjęciu początków uzwojeń jak na rysunku wynikają następujące równania opisujące obwód | |||
<math>U_1=jX_l_1I_1+jX_MI_2</math> | |||
<math>U_2=-[jX_L_2I_2+jX_MI_1]</math> | |||
Znak minus występujący we wzorze na <math>U_2\,</math> wynika z kierunku <math>U_2\,</math> zaznaczonego na rysunku Z równań wynika następujący wzór określający napięcie wyjściowe | |||
<math>U_2=-[\frac{X_M}{X_{L1}}U_1+jI_2(\frac{X_{L1}X_{L2}-X_M^2}{X_{L1}})]</math> | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 10:44, 1 sie 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
|
|
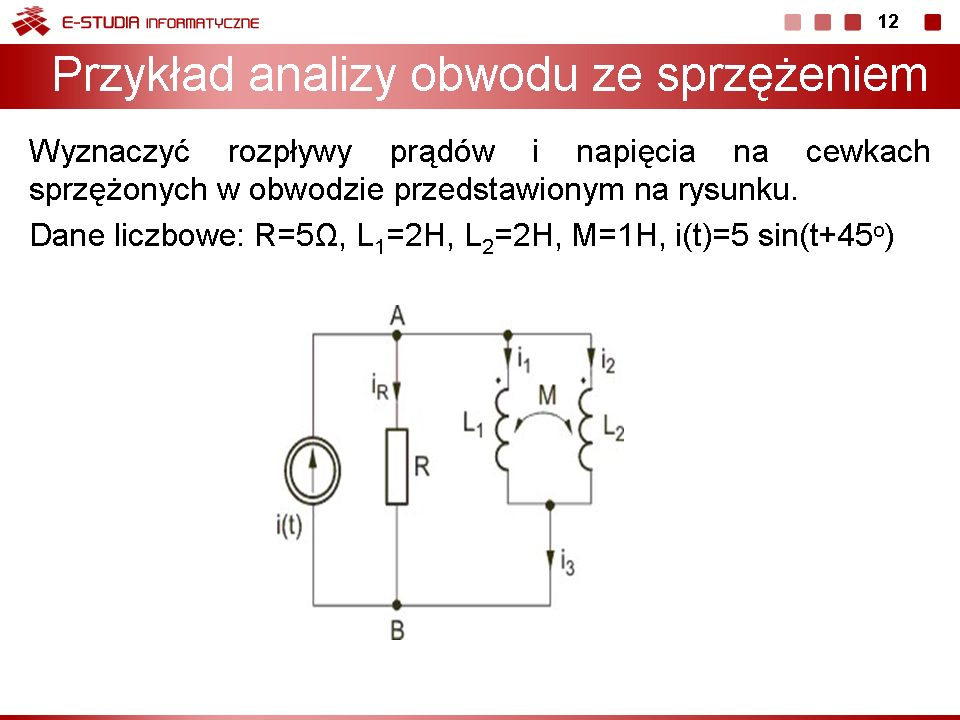
PRZYKŁAD
Wyznaczyć rozpływy prądów w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Rozwiązanie
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono na rysunku |

|
Wielkości symboliczne charakteryzujące elementy obwodu:
Impedancja zastępcza obwodu wobec
|