PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 277: | Linia 277: | ||
Uzwojenie, do którego jest zazwyczaj doprowadzone źródło energii elektrycznej, nazywamy uzwojeniem pierwotnym, natomiast uzwojenie, do którego jest dołączony odbiornik, nazywamy uzwojeniem wtórnym. Zaciski uzwojenia pierwotnego stanowią wejście układu, a zaciski uzwojenia wtórnego - wyjście. Odpowiednie napięcia i prądy w transformatorze nazywamy pierwotnymi lub wtórnymi. Wszystkie wielkości i parametry związane z uzwojeniem pierwotnym opatrzymy wskaźnikiem 1, a wielkości i parametry związane z uzwojeniem wtórnym – wskaźnikiem 2. | Uzwojenie, do którego jest zazwyczaj doprowadzone źródło energii elektrycznej, nazywamy uzwojeniem pierwotnym, natomiast uzwojenie, do którego jest dołączony odbiornik, nazywamy uzwojeniem wtórnym. Zaciski uzwojenia pierwotnego stanowią wejście układu, a zaciski uzwojenia wtórnego - wyjście. Odpowiednie napięcia i prądy w transformatorze nazywamy pierwotnymi lub wtórnymi. Wszystkie wielkości i parametry związane z uzwojeniem pierwotnym opatrzymy wskaźnikiem 1, a wielkości i parametry związane z uzwojeniem wtórnym – wskaźnikiem 2. | ||
Do uzwojenia pierwotnego przyłożone jest napięcie sinusoidalnie zmienne o wartości chwilowej <math>u_1(t)\,</math>. Wartość chwilową prądu w uzwojeniu pierwotnym oznaczymy przez <math>i_1(t)\,</math> Pod wpływem zmiennego w czasie prądu <math>i_1(t)\,</math> w przestrzeni otaczającej uzwojenie powstaje zmienny strumień magnetyczny <math>\phi\,</math> , będący superpozycją strumieni | Do uzwojenia pierwotnego przyłożone jest napięcie sinusoidalnie zmienne o wartości chwilowej <math>u_1(t)\,</math>. Wartość chwilową prądu w uzwojeniu pierwotnym oznaczymy przez <math>i_1(t)\,</math> Pod wpływem zmiennego w czasie prądu <math>i_1(t)\,</math> w przestrzeni otaczającej uzwojenie powstaje zmienny strumień magnetyczny <math>\phi\,</math> , będący superpozycją strumieni <math>\phi_1 i \phi_2</math> . Przy założeniu jego równomiernego rozkładu na przekroju S, strumień jest iloczynem indukcji magnetycznej B i przekroju S,<math>\phi =BS</math> Strumień ten kojarzy się zarówno z uzwojeniem pierwotnym o liczbie zwojów <math>z_1\,</math> wytwarzając strumień skojarzony <math>\psi_1=z_1\phi</math>, jak i uzwojeniem wtórnym o liczbie zwojów z2 wytwarzając w nim strumień skojarzony <math>\psi_1=z_1\phi</math> Zgodne z prawem indukcji elektromagnetycznej pod wpływem zmiennego w czasie strumienia magnetycznego indukuje się napięcie<math> u(t)\,</math> | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 10:26, 1 sie 2006

|
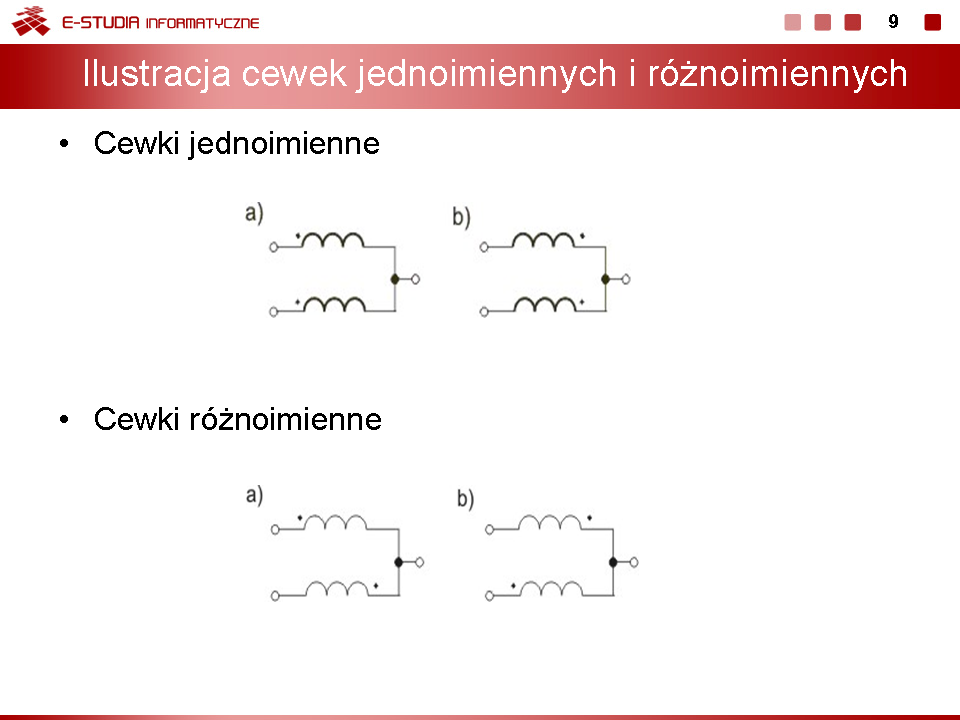
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
|
|
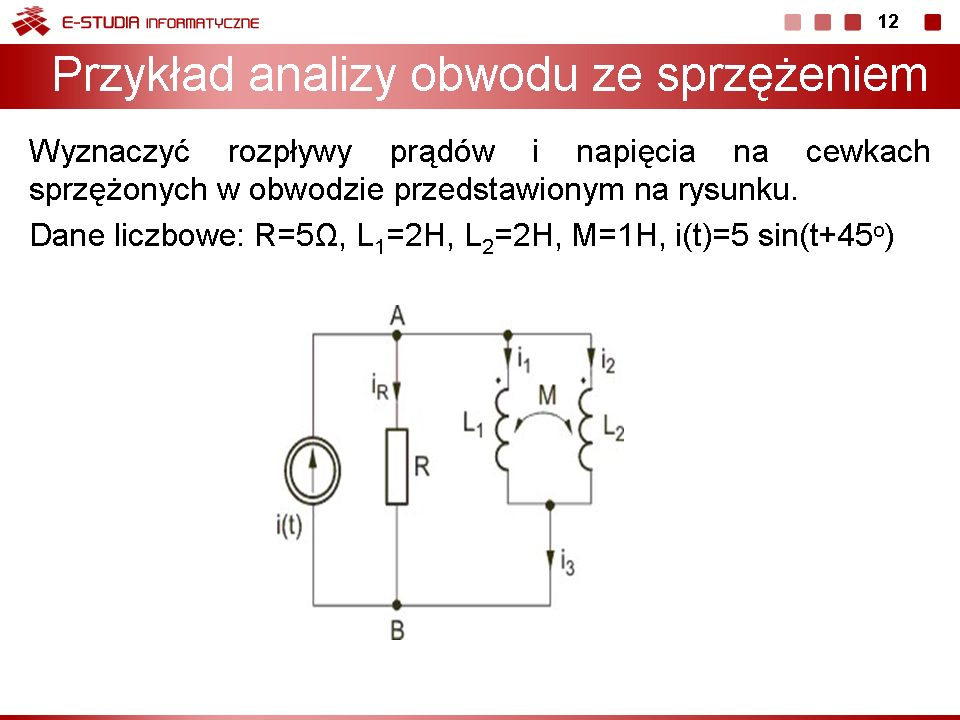
PRZYKŁAD
Wyznaczyć rozpływy prądów w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Rozwiązanie
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono na rysunku |

|
Wielkości symboliczne charakteryzujące elementy obwodu:
Impedancja zastępcza obwodu wobec
|