PF Moduł 12: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „\displaystyle ” na „” |
m Zastępowanie tekstu – „,</math>” na „</math>,” |
||
| Linia 16: | Linia 16: | ||
Prąd elektryczny to uporządkowany ruch ładunków elektrycznych pod wpływem pola elektrycznego. Nośnikami prądu mogą być ładunki dodatnie (np. jony w cieczy lub w gazie) i ładunki ujemne (elektrony w ciele stałym, elektrony i jony w cieczy lub w gazie). Jako kierunek prądu przyjęto kierunek ruchu nośników dodatnich, a więc prąd płynie od potencjału wyższego do potencjału niższego. | Prąd elektryczny to uporządkowany ruch ładunków elektrycznych pod wpływem pola elektrycznego. Nośnikami prądu mogą być ładunki dodatnie (np. jony w cieczy lub w gazie) i ładunki ujemne (elektrony w ciele stałym, elektrony i jony w cieczy lub w gazie). Jako kierunek prądu przyjęto kierunek ruchu nośników dodatnich, a więc prąd płynie od potencjału wyższego do potencjału niższego. | ||
'''Natężenie prądu''' jest określone jako szybkość przepływu ładunku, czyli stosunek ładunku <math>dq\ | '''Natężenie prądu''' jest określone jako szybkość przepływu ładunku, czyli stosunek ładunku <math>dq\</math>, przepływającego przez przekrój poprzeczny przewodnika w czasie <math>dt\</math>,, do tego czasu | ||
Jeśli w przepływie prądu uczestniczą różne nośniki ładunku, to natężenia prądu tych nośników dodają się. | Jeśli w przepływie prądu uczestniczą różne nośniki ładunku, to natężenia prądu tych nośników dodają się. | ||
Gęstość prądu jest wektorem, którego kierunek jest zgodny z kierunkiem przepływu prądu, zaś wartość jest określona przez stosunek natężenia prądu <math>dI\ | Gęstość prądu jest wektorem, którego kierunek jest zgodny z kierunkiem przepływu prądu, zaś wartość jest określona przez stosunek natężenia prądu <math>dI\</math>, przepływającego przez mały element powierzchni przekroju poprzecznego przewodnika <math>dS_{\perp}\</math>, do pola powierzchni tego elementu. | ||
Zatem <math>\overrightarrow{j}=j\overrightarrow{w}</math> , gdzie <math>\overrightarrow{w}\ | Zatem <math>\overrightarrow{j}=j\overrightarrow{w}</math> , gdzie <math>\overrightarrow{w}\</math>, jest wersorem wskazującym kierunek ruchu dodatnich nośników prądu przez powierzchnię <math>dS_{\perp}\</math>,. Natężenie prądu jest strumieniem wektora gęstości prądu przez daną powierzchnię. | ||
|} | |} | ||
| Linia 33: | Linia 33: | ||
Dla danego przewodnika stosunek napięcia między końcami przewodnika do natężenia prądu płynącego przez przewodnik jest wielkością stałą. Wielkość tę nazywamy oporem elektrycznym. | Dla danego przewodnika stosunek napięcia między końcami przewodnika do natężenia prądu płynącego przez przewodnik jest wielkością stałą. Wielkość tę nazywamy oporem elektrycznym. | ||
Z prawa tego wynika, że dla przewodnika natężenie prądu jest liniową funkcją napięcia, współczynnik kierunkowy prostej <math>I(U)\ | Z prawa tego wynika, że dla przewodnika natężenie prądu jest liniową funkcją napięcia, współczynnik kierunkowy prostej <math>I(U)\</math>, jest równy odwrotności oporu. | ||
Istnieją elementy przewodzące prąd dla których natężenie prądu nie jest liniową funkcją napięcia. | Istnieją elementy przewodzące prąd dla których natężenie prądu nie jest liniową funkcją napięcia. | ||
| Linia 45: | Linia 45: | ||
|valign="top"|'''12.3 Opór elektryczny''' | |valign="top"|'''12.3 Opór elektryczny''' | ||
'''Opór elektryczny''' jednorodnego przewodnika o stałym przekroju jest zależny od jego długości <math>l\ | '''Opór elektryczny''' jednorodnego przewodnika o stałym przekroju jest zależny od jego długości <math>l\</math>, i pola przekroju <math>S\</math>, oraz od rodzaju przewodnika, gdzie <math>\rho\</math>, to '''opór właściwy''' substancji, z której wykonany jest przewodnik. | ||
Wartość oporu właściwego silnie zależy od własności mikroskopowych substancji, z których wynika rodzaj nośników prądu (ładunek i masa) oraz ich koncentracja (liczba nośników w jednostce objętości). W przewodnikach (metalach) nośnikami są elektrony. Ich koncentracja jest duża, tego rzędu co koncentracja atomów, stąd małe wartości oporu właściwego. | Wartość oporu właściwego silnie zależy od własności mikroskopowych substancji, z których wynika rodzaj nośników prądu (ładunek i masa) oraz ich koncentracja (liczba nośników w jednostce objętości). W przewodnikach (metalach) nośnikami są elektrony. Ich koncentracja jest duża, tego rzędu co koncentracja atomów, stąd małe wartości oporu właściwego. | ||
Opór właściwy metali rośnie wraz ze wzrostem temperatury. Wg. najprostszego modelu zależność ta ma charakter liniowy, gdzie <math>\alpha\ | Opór właściwy metali rośnie wraz ze wzrostem temperatury. Wg. najprostszego modelu zależność ta ma charakter liniowy, gdzie <math>\alpha\</math>, jest temperaturowym współczynnikiem oporu. | ||
W izolatorach (dielektrykach) koncentracja nośników jest mała, stąd duże wartości oporu właściwego. | W izolatorach (dielektrykach) koncentracja nośników jest mała, stąd duże wartości oporu właściwego. | ||
| Linia 57: | Linia 57: | ||
W półprzewodnikach samoistnych (np. german, krzem) koncentracja nośników (elektrony i dziury) rośnie ze wzrostem temperatury, co prowadzi do zmniejszania wartości oporu właściwego. Silny wpływ na koncentrację nośników mają domieszki. | W półprzewodnikach samoistnych (np. german, krzem) koncentracja nośników (elektrony i dziury) rośnie ze wzrostem temperatury, co prowadzi do zmniejszania wartości oporu właściwego. Silny wpływ na koncentrację nośników mają domieszki. | ||
'''Przewodnictwo właściwe''' <math>\sigma\ | '''Przewodnictwo właściwe''' <math>\sigma\</math>, to odwrotność oporu właściwego <math>\rho\</math>,. | ||
|} | |} | ||
| Linia 67: | Linia 67: | ||
|valign="top"|'''12.4 Mikroskopowy opis przepływu prądu elektrycznego w przewodniku.''' | |valign="top"|'''12.4 Mikroskopowy opis przepływu prądu elektrycznego w przewodniku.''' | ||
W jednorodnym przewodzie o przekroju <math>S\ | W jednorodnym przewodzie o przekroju <math>S\</math>, i koncentracji elektronów <math>n\</math>, pole elektryczne działa na elektrony siłą <math>\overrightarrow{F}=-e\overrightarrow{E}</math> , zmuszając je do określonego ruchu. Natężenie prądu można wyznaczyć licząc ile elektronów przepłynie w czasie <math>dt\</math>, przez wybrany przekrój przewodu. Prowadzi to do wzorów określających natężenie prądu i powierzchniową gęstość prądu, gdzie <math>n\</math>, jest koncentracją elektronów (liczba elektronów w jednostce objętości przewodnika), <math>e\</math>, - ładunkiem elementarnym, zaś <math>u\</math>, - prędkością unoszenia elektronów w kierunku wymuszonym przez pole elektryczne. Wzór określający zależność gęstości prądu od natężenia pola elektrycznego jest równoważny prawu Ohma. | ||
Poruszając się w kierunku wymuszonym przez pole elektryczne elektrony nie rezygnują z bezładnego ruchu cieplnego. Według prostego modelu klasycznego „gaz” elektronowy opisujemy podobnie jak gaz doskonały. Oznaczmy przez v średnią prędkość ruchu cieplnego elektronów w przewodniku, a przez <math>u\ | Poruszając się w kierunku wymuszonym przez pole elektryczne elektrony nie rezygnują z bezładnego ruchu cieplnego. Według prostego modelu klasycznego „gaz” elektronowy opisujemy podobnie jak gaz doskonały. Oznaczmy przez v średnią prędkość ruchu cieplnego elektronów w przewodniku, a przez <math>u\</math>, średnią prędkość unoszenia elektronów w tym przewodniku, gdy płynie w nim prąd stały. Przewodnik znajduje się w temperaturze pokojowej. | ||
Wartość prędkości średniej ruchu cieplnego można oszacować wykorzystując wzory: | Wartość prędkości średniej ruchu cieplnego można oszacować wykorzystując wzory: | ||
| Linia 77: | Linia 77: | ||
wartość prędkości unoszenia elektronów można oszacować wykorzystując wzory | wartość prędkości unoszenia elektronów można oszacować wykorzystując wzory | ||
:<math>\begin{matrix}I=neuS & \Longrightarrow &u=\frac{I}{neS}\approx 2\cdot 10^{-5} m/s \end{matrix}</math> dla typowych wartości <math>I, n, S\ | :<math>\begin{matrix}I=neuS & \Longrightarrow &u=\frac{I}{neS}\approx 2\cdot 10^{-5} m/s \end{matrix}</math> dla typowych wartości <math>I, n, S\</math>,: | ||
<math>I = 1A\ | <math>I = 1A\</math>,, grubość miedzianego przewodu <math>d = 2mm\</math>,, <math>n = 8,5\cdot 10^{28}/m3</math> | ||
(każdy atom miedzi daje jeden elektron swobodny, zatem znając masę molową miedzi <math>\mu= 63,5g/mol</math>, gęstość miedzi <math>\rho= 8,96g/cm^3</math> i liczbę Avogadro <math>N_A = 6,02\cdot 1023/mol</math> można obliczyć koncentrację elektronów <math>n\ | (każdy atom miedzi daje jeden elektron swobodny, zatem znając masę molową miedzi <math>\mu= 63,5g/mol</math>, gęstość miedzi <math>\rho= 8,96g/cm^3</math> i liczbę Avogadro <math>N_A = 6,02\cdot 1023/mol</math> można obliczyć koncentrację elektronów <math>n\</math>,). | ||
Warto zauważyć, że prędkość elektronów będących nośnikami prądu jest niezwykle mała w porównaniu z prędkością ruchu cieplnego. Można powiedzieć, że prąd płynie bardzo wolno. Oczywiście sygnał, który nakazuje elektronom przewodnictwa płynąć w określonym kierunku rozchodzi się niezwykle szybko. Sygnałem tym jest pole elektryczne, które rozchodzi się z prędkością równą prędkości światła. | Warto zauważyć, że prędkość elektronów będących nośnikami prądu jest niezwykle mała w porównaniu z prędkością ruchu cieplnego. Można powiedzieć, że prąd płynie bardzo wolno. Oczywiście sygnał, który nakazuje elektronom przewodnictwa płynąć w określonym kierunku rozchodzi się niezwykle szybko. Sygnałem tym jest pole elektryczne, które rozchodzi się z prędkością równą prędkości światła. | ||
| Linia 95: | Linia 95: | ||
|valign="top"|'''12.5 Praca i moc''' | |valign="top"|'''12.5 Praca i moc''' | ||
'''Praca''' <math>dW\ | '''Praca''' <math>dW\</math>, wykonana przez pole elektryczne na wymuszenie przepływu ładunku dq w czasie <math>dt\</math>, powoduje wzrost energii wewnętrznej przewodnika (wzrost temperatury), a w konsekwencji do otoczenia może przepłynąć ciepło <math>dQ =dW</math>. | ||
Pracę wykonaną w czasie <math>t\ | Pracę wykonaną w czasie <math>t\</math>, otrzymamy po zsumowaniu porcji <math>dW\</math>,, które w przypadku prądu o stałym natężeniu daje wartość <math>W=UIt</math>. Wykorzystując prawo Ohma wzór ten można przedstawić w trzech postaciach. | ||
'''Moc''' jest równa szybkości wykonywania pracy i może być przedstawiona za pomocą trzech wzorów. | '''Moc''' jest równa szybkości wykonywania pracy i może być przedstawiona za pomocą trzech wzorów. | ||
| Linia 111: | Linia 111: | ||
|valign="top"|'''12.6 Siła elektromotoryczna ''' | |valign="top"|'''12.6 Siła elektromotoryczna ''' | ||
Siła elektromotoryczna jest różnicą potencjałów wytwarzaną przez źródło prądu, czyli urządzenie przetwarzające energię (chemiczną, mechaniczną, ...) na energię elektryczną. Jej wartość jest określona przez wydatek energetyczny źródła <math>dW\ | Siła elektromotoryczna jest różnicą potencjałów wytwarzaną przez źródło prądu, czyli urządzenie przetwarzające energię (chemiczną, mechaniczną, ...) na energię elektryczną. Jej wartość jest określona przez wydatek energetyczny źródła <math>dW\</math>, na wymuszenie przepływu ładunku <math>dq\</math>,, przypadający na jednostkę ładunku. | ||
Większe znaczenie praktyczne ma określenie siły elektromotorycznej jako napięcia na zaciskach źródła, gdy prąd w obwodzie zawierającym źródło nie płynie. | Większe znaczenie praktyczne ma określenie siły elektromotorycznej jako napięcia na zaciskach źródła, gdy prąd w obwodzie zawierającym źródło nie płynie. | ||
| Linia 135: | Linia 135: | ||
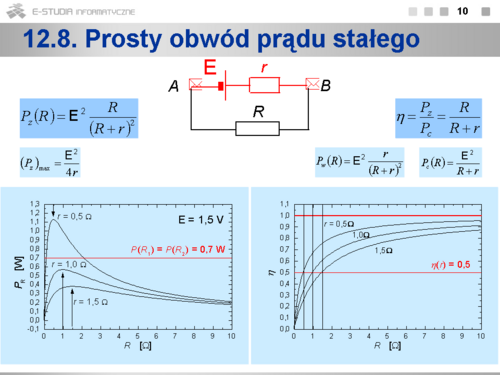
|valign="top"|'''12.8 Prosty obwód prądu stałego''' | |valign="top"|'''12.8 Prosty obwód prądu stałego''' | ||
Składa się w swojej podstawowej wersji ze źródła o sile elektromotorycznej <math>E\ | Składa się w swojej podstawowej wersji ze źródła o sile elektromotorycznej <math>E\</math>, i oporze wewnętrznym <math>r\</math>, oraz obwodu zewnętrznego o oporze <math>R\</math>,. | ||
Natężenie prądu w obwodzie osiąga wartość największą dla <math>R = 0</math>, jest to tzw. prąd zwarcia <math>I_z\ | Natężenie prądu w obwodzie osiąga wartość największą dla <math>R = 0</math>, jest to tzw. prąd zwarcia <math>I_z\</math>,. | ||
Napięcie na zaciskach źródła <math>U_{AB}\ | Napięcie na zaciskach źródła <math>U_{AB}\</math>, dąży do wartości równej sile elektromotorycznej, gdy <math>R\to \infty\</math>, . | ||
Moc w oporniku zewnętrznym <math>R\ | Moc w oporniku zewnętrznym <math>R\</math>, osiąga wartość największą dla <math>R=r</math>. | ||
Moc całkowita <math>P_c\ | Moc całkowita <math>P_c\</math>, jest równa sumie mocy <math>P_z\</math>, w obwodzie zewnętrznym i mocy <math>P_w\</math>, wewnątrz źródła: | ||
:<math>P_c(R)=P_z(R)+P_w(R)</math> | :<math>P_c(R)=P_z(R)+P_w(R)</math> | ||
| Linia 151: | Linia 151: | ||
Na rysunkach zostały przedstawione przykładowe wykresy zależności natężenia prądu, napięcia na zaciskach źródła, mocy w obwodzie zewnętrznym i sprawności od wartości oporu zewnętrznego. | Na rysunkach zostały przedstawione przykładowe wykresy zależności natężenia prądu, napięcia na zaciskach źródła, mocy w obwodzie zewnętrznym i sprawności od wartości oporu zewnętrznego. | ||
Z charakteru zależności mocy w obwodzie zewnętrznym od wartości oporu zewnętrznego wynika, że określoną moc P można uzyskać dla dwóch różnych wartości oporu <math>R_1<r\ | Z charakteru zależności mocy w obwodzie zewnętrznym od wartości oporu zewnętrznego wynika, że określoną moc P można uzyskać dla dwóch różnych wartości oporu <math>R_1<r\</math>, i <math>R_2>r\</math>,. Na podstawie wykresu zależności sprawności od oporu zewnętrznego można stwierdzić, że bardziej korzystny jest wybór oporu <math>R > r\</math>,, gdyż większa jest sprawność. | ||
|} | |} | ||
| Linia 165: | Linia 165: | ||
'''Obliczanie oporu zastępczego układu oporników''' | '''Obliczanie oporu zastępczego układu oporników''' | ||
Jeśli układ oporników podłączymy do źródła napięcia <math>U_0\ | Jeśli układ oporników podłączymy do źródła napięcia <math>U_0\</math>, to popłynie prąd o natężeniu <math>I\</math>,. Opór zastępczy układu, to opór opornika, przez który po podłączeniu do takiego źródła popłynie prąd o takim samym natężeniu. | ||
Wynika stąd ogólna i uniwersalna metoda obliczania oporu zastępczego: należy obliczyć natężenie prądu, który popłynie do danego układu oporników po podłączeniu do źródła napięcia <math>U_0\ | Wynika stąd ogólna i uniwersalna metoda obliczania oporu zastępczego: należy obliczyć natężenie prądu, który popłynie do danego układu oporników po podłączeniu do źródła napięcia <math>U_0\</math>,. To natężenie prądu będzie proporcjonalne do napięcia, a współczynnik proporcjonalności to odwrotność oporu zastępczego układu <math>I=\frac{1}{R}\cdot U_0</math> . Za pomocą tej metody można obliczyć opór dowolnego układu oporników, bez konieczności ustalania jak są połączone oporniki, a więc nawet bez znajomości wzorów na łączenie szeregowe, równoległe, łączenia w trójkąt i w gwiazdę, ... . Do obliczania natężenia prądu <math>I\</math>, wykorzystywane są dwa podstawowe prawa fizyczne: | ||
*zasada zachowania ładunku (czyli tzw. pierwsze prawo Kirchhoffa), | *zasada zachowania ładunku (czyli tzw. pierwsze prawo Kirchhoffa), | ||
| Linia 174: | Linia 174: | ||
Spośród różnych możliwych połączeń oporników wyróżniamy dwa podstawowe - połączenie szeregowe i połączenie równoległe. | Spośród różnych możliwych połączeń oporników wyróżniamy dwa podstawowe - połączenie szeregowe i połączenie równoległe. | ||
'''Szeregowe połączenie oporników.''' Oporniki uznajemy za połączone szeregowo, jeżeli płynie przez nie prąd o takim samym natężeniu. Układ <math>n\ | '''Szeregowe połączenie oporników.''' Oporniki uznajemy za połączone szeregowo, jeżeli płynie przez nie prąd o takim samym natężeniu. Układ <math>n\</math>, oporników połączonych szeregowo można zastąpić opornikiem o oporze równym sumie ich oporów | ||
'''Równoległe połączenie oporników.''' Oporniki uznajemy za połączone równolegle, jeżeli napięcie na nich ma taką samą wartość. Układ <math>n\ | '''Równoległe połączenie oporników.''' Oporniki uznajemy za połączone równolegle, jeżeli napięcie na nich ma taką samą wartość. Układ <math>n\</math>, oporników połączonych równolegle można zastąpić opornikiem o oporze, którego odwrotność jest równa sumie odwrotności ich oporów | ||
Układy oporników spotykane w zadaniach są często zagmatwane. Aby obliczyć opór takiego układu, staramy się narysować go w prostszy sposób, ustalając które oporniki są połączone szeregowo a które równolegle. Układ oporników można oczywiście przekształcać tylko w taki sposób, aby natężenia prądów płynących przez poszczególne oporniki nie uległy zmianie. | Układy oporników spotykane w zadaniach są często zagmatwane. Aby obliczyć opór takiego układu, staramy się narysować go w prostszy sposób, ustalając które oporniki są połączone szeregowo a które równolegle. Układ oporników można oczywiście przekształcać tylko w taki sposób, aby natężenia prądów płynących przez poszczególne oporniki nie uległy zmianie. | ||
| Linia 199: | Linia 199: | ||
'''Łączenie źródeł napięcia''' | '''Łączenie źródeł napięcia''' | ||
Podstawowe sposoby połączenia <math>n\ | Podstawowe sposoby połączenia <math>n\</math>, źródeł napięcia o sile elektromotorycznej <math>E\</math>, i oporności wewnętrznej <math>r\</math>, w baterię to połączenie szeregowe i połączenie równoległe. | ||
W przypadku połączenia szeregowego siła elektromotoryczna baterii jest sumą sił elektromotorycznych źródeł, opór wewnętrzny baterii jest sumą oporów wewnętrznych źródeł. | W przypadku połączenia szeregowego siła elektromotoryczna baterii jest sumą sił elektromotorycznych źródeł, opór wewnętrzny baterii jest sumą oporów wewnętrznych źródeł. | ||
| Linia 240: | Linia 240: | ||
'''Przykład 12.2''' | '''Przykład 12.2''' | ||
Kondensator składa się z dwóch kulistych, współśrodkowych powierzchni metalowych. Przestrzeń między tymi powierzchniami wypełniona jest ebonitem. Kondensator naładowano ładunkiem <math>Q\ | Kondensator składa się z dwóch kulistych, współśrodkowych powierzchni metalowych. Przestrzeń między tymi powierzchniami wypełniona jest ebonitem. Kondensator naładowano ładunkiem <math>Q\</math>,. Po jakim czasie od chwili naładowania ładunek zmaleje o połowę? Względna przenikalność elektryczna ebonitu wynosi <math>\varepsilon_r = 3,1</math> a oporność właściwa <math>\rho = 10^{13} \Omega \cdot m</math>. | ||
| Linia 263: | Linia 263: | ||
:<math>\begin{matrix}Q(t)=Q_0e^{-t/{\tau}}; &\tau=\varepsilon_0\varepsilon_r\rho \approx 274s \end{matrix}</math> | :<math>\begin{matrix}Q(t)=Q_0e^{-t/{\tau}}; &\tau=\varepsilon_0\varepsilon_r\rho \approx 274s \end{matrix}</math> | ||
Pojemność kondensatora kulistego i opór warstwy kulistej zależą od parametrów geometrycznych oraz odpowiedniego parametru substancji. Iloczyn pojemności i oporu (stała czasowa rozładowania kondensatora) zależy tylko od stałych materiałowych: <math>\varepsilon_r\ | Pojemność kondensatora kulistego i opór warstwy kulistej zależą od parametrów geometrycznych oraz odpowiedniego parametru substancji. Iloczyn pojemności i oporu (stała czasowa rozładowania kondensatora) zależy tylko od stałych materiałowych: <math>\varepsilon_r\</math>, i <math>\rho\</math>, . | ||
:<math>\begin{matrix}Q(t_{1/2})= \frac{Q_0}{2}; &t_{1/2}=\tau ln2\approx 190s \end{matrix}</math> | :<math>\begin{matrix}Q(t_{1/2})= \frac{Q_0}{2}; &t_{1/2}=\tau ln2\approx 190s \end{matrix}</math> | ||
| Linia 275: | Linia 275: | ||
= Zadania = | = Zadania = | ||
'''1.''' Dwie kule metalowe o promieniu a umieszczono w ośrodku przewodzącym o stałej oporności właściwej <math>\rho\ | '''1.''' Dwie kule metalowe o promieniu a umieszczono w ośrodku przewodzącym o stałej oporności właściwej <math>\rho\</math>,, odległość między ich środkami wynosi <math>d >> a</math>. Obliczyć natężenie prądu, jaki popłynie podłączeniu kul do źródła stałego napięcia <math>U\</math>,. | ||
| Linia 286: | Linia 286: | ||
<hr width="100%"> | <hr width="100%"> | ||
'''2.''' Do źródła prądu o oporze wewnętrznym <math>r = 1\Omega</math> podłączono dwa jednakowe oporniki <math>R\ | '''2.''' Do źródła prądu o oporze wewnętrznym <math>r = 1\Omega</math> podłączono dwa jednakowe oporniki <math>R\</math>, połączone raz szeregowo, a raz równolegle. W obu przypadkach otrzymano taką samą moc <math>P\</math>, w obwodzie zewnętrznym. Obliczyć wartość oporności <math>R\</math>,. Jaką część mocy całkowitej stanowi moc <math>P\</math>, w obu przypadkach? Ile razy moc <math>P\</math>, jest mniejsza od maksymalnej mocy, jaką można uzyskać z tego źródła na oporniku zewnętrznym? | ||
| Linia 297: | Linia 297: | ||
<hr width="100%"> | <hr width="100%"> | ||
'''3.''' Z drutu o średnicy <math>d\ | '''3.''' Z drutu o średnicy <math>d\</math>, i oporze właściwym <math>\rho\</math>, , zrobiono sześcian o krawędzi <math>a\</math>,. Obliczyć opór zastępczy, gdy napięcie <math>U_0\</math>, jest podłączone: | ||
:'''a.''' do wierzchołków leżących na końcach przekątnej sześcianu, | :'''a.''' do wierzchołków leżących na końcach przekątnej sześcianu, | ||
| Linia 314: | Linia 314: | ||
<hr width="100%"> | <hr width="100%"> | ||
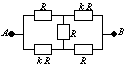
'''4.''' Obliczyć natężenia prądu płynącego przez oporniki oraz opór zastępczy <math>R_{AB}\ | '''4.''' Obliczyć natężenia prądu płynącego przez oporniki oraz opór zastępczy <math>R_{AB}\</math>, układu oporników przedstawionego na rysunku, po podłączeniu źródła napięcia <math>U\</math>,. Dane są: <math>U,\, R\, i\, k\in R_{+}</math>. Przedyskutować zależność oporu <math>R_{AB}\</math>, od wartości parametru <math>k\</math>,. | ||
:[[Grafika:PF_M12_Zad_Rys1.png]] | :[[Grafika:PF_M12_Zad_Rys1.png]] | ||
| Linia 330: | Linia 330: | ||
Dla <math>k = 0</math> opór układu przyjmuje wartość <math>R_{AB} = R/3</math>, a więc mamy układ trzech oporników połączonych równolegle. | Dla <math>k = 0</math> opór układu przyjmuje wartość <math>R_{AB} = R/3</math>, a więc mamy układ trzech oporników połączonych równolegle. | ||
Dla <math>k = 1</math> opór układu przyjmuje wartość <math>R\ | Dla <math>k = 1</math> opór układu przyjmuje wartość <math>R\</math>,. Ponieważ przez środkowy opornik prąd nie płynie (natężenie prądu </math>I_3 = 0</math>), układ składa się z dwóch równoległych gałęzi oporników połączonych szeregowo. | ||
Dla <math>k\to \infty\ | Dla <math>k\to \infty\</math>, opór układu dąży do wartości <math>3R\</math>,, natężenie prądu <math>I_2\</math>, do zera, a więc mamy układ trzech oporników połączonych szeregowo. | ||
Z dyskusji rozwiązania wynika, że opór tego układu oporników zawiera się w przedziale | Z dyskusji rozwiązania wynika, że opór tego układu oporników zawiera się w przedziale | ||
Wersja z 09:36, 5 wrz 2023
Wykład
 |
Materiały do ćwiczeń
Przykład 12.1
W przedstawionym obwodzie przewody łączące oporniki mają opór bliski zeru.
Obliczyć natężenie prądu w przewodzie AB. Dane: U, R
Przykład 12.2
Kondensator składa się z dwóch kulistych, współśrodkowych powierzchni metalowych. Przestrzeń między tymi powierzchniami wypełniona jest ebonitem. Kondensator naładowano ładunkiem Parser nie mógł rozpoznać (błąd składni): {\displaystyle Q\} ,. Po jakim czasie od chwili naładowania ładunek zmaleje o połowę? Względna przenikalność elektryczna ebonitu wynosi a oporność właściwa .
Zadania
1. Dwie kule metalowe o promieniu a umieszczono w ośrodku przewodzącym o stałej oporności właściwej Parser nie mógł rozpoznać (błąd składni): {\displaystyle \rho\} ,, odległość między ich środkami wynosi . Obliczyć natężenie prądu, jaki popłynie podłączeniu kul do źródła stałego napięcia Parser nie mógł rozpoznać (błąd składni): {\displaystyle U\} ,.
2. Do źródła prądu o oporze wewnętrznym podłączono dwa jednakowe oporniki Parser nie mógł rozpoznać (błąd składni): {\displaystyle R\} , połączone raz szeregowo, a raz równolegle. W obu przypadkach otrzymano taką samą moc Parser nie mógł rozpoznać (błąd składni): {\displaystyle P\} , w obwodzie zewnętrznym. Obliczyć wartość oporności Parser nie mógł rozpoznać (błąd składni): {\displaystyle R\} ,. Jaką część mocy całkowitej stanowi moc Parser nie mógł rozpoznać (błąd składni): {\displaystyle P\} , w obu przypadkach? Ile razy moc Parser nie mógł rozpoznać (błąd składni): {\displaystyle P\} , jest mniejsza od maksymalnej mocy, jaką można uzyskać z tego źródła na oporniku zewnętrznym?
3. Z drutu o średnicy Parser nie mógł rozpoznać (błąd składni): {\displaystyle d\} , i oporze właściwym Parser nie mógł rozpoznać (błąd składni): {\displaystyle \rho\} , , zrobiono sześcian o krawędzi Parser nie mógł rozpoznać (błąd składni): {\displaystyle a\} ,. Obliczyć opór zastępczy, gdy napięcie Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_0\} , jest podłączone:
- a. do wierzchołków leżących na końcach przekątnej sześcianu,
- b. do wierzchołków leżących na końcach krawędzi sześcianu,
- c. do wierzchołków leżących na końcach przekątnej ściany bocznej sześcianu.
4. Obliczyć natężenia prądu płynącego przez oporniki oraz opór zastępczy Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_{AB}\} , układu oporników przedstawionego na rysunku, po podłączeniu źródła napięcia Parser nie mógł rozpoznać (błąd składni): {\displaystyle U\} ,. Dane są: . Przedyskutować zależność oporu Parser nie mógł rozpoznać (błąd składni): {\displaystyle R_{AB}\} , od wartości parametru Parser nie mógł rozpoznać (błąd składni): {\displaystyle k\} ,.
Słowa kluczowe
- natężenie prądu
- gęstość prądu
- prawo Ohma
- opór elektryczny
- opór właściwy
- przewodnictwo właściwe
- koncentracja nośników prądu
- prędkość unoszenia
- praca i moc prądu
- siła elektromotoryczna
- opór wewnętrzny źródła
- prawa Kirchhoffa
- opór zastępczy