PEE Moduł 6: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 138: | Linia 138: | ||
|valign="top"|'''Układ gwiazdowy faz generatora i odbiornika''' | |valign="top"|'''Układ gwiazdowy faz generatora i odbiornika''' | ||
Rozpatrzmy układ połączeń gwiazdowych odbiornika i generatora (gwiazda-gwiazda) z oznaczeniami prądów i napięć przedstawionymi na | Rozpatrzmy układ połączeń gwiazdowych odbiornika i generatora (gwiazda-gwiazda) z oznaczeniami prądów i napięć przedstawionymi na rysunku obok (slajd nr 10). | ||
Punkt 0 oznacza punkt wspólny faz generatora. Punkt <math>N\,</math> jest punktem wspólnym impedancji fazowych odbiornika. Zakładamy symetrię napięć fazowych generatora i dowolne wartości impedancji odbiornika. Przyjmijmy do analizy układ czteroprzewodowy z impedancją przewodu zerowego równa <math>Z_N</math>. Wartość impedancji <math>Z_N</math> może być dowolna, w szczególności zerowa (bezpośrednie zwarcie punktów wspólnych generatora i odbiornika) lub nieskończona (układ trójprzewodowy bez przewodu zerowego). Napięcie między punktem zerowym odbiornika i generatora oznaczymy przez <math>U_N</math> i nazywać będziemy '''napięciem niezrównoważenia'''. | |||
|} | |} | ||
| Linia 146: | Linia 147: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd11.png]] | ||
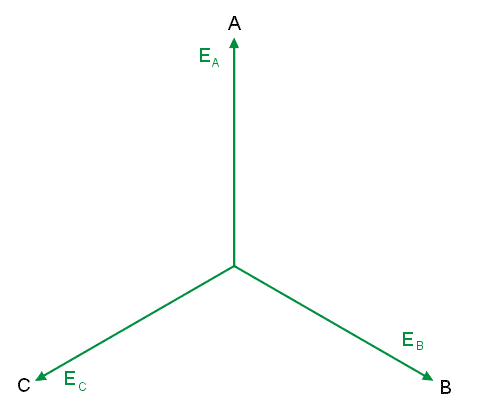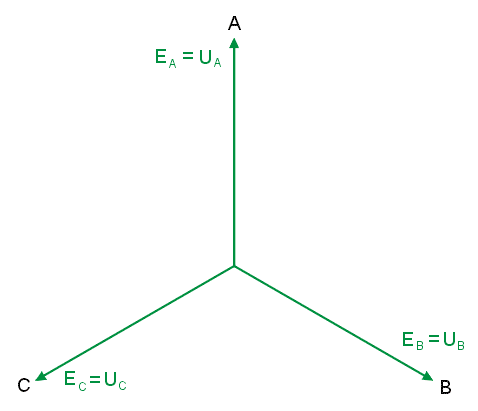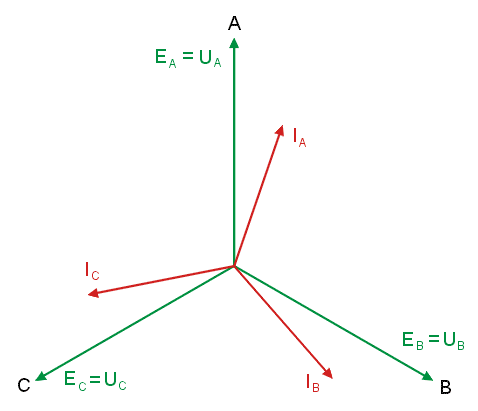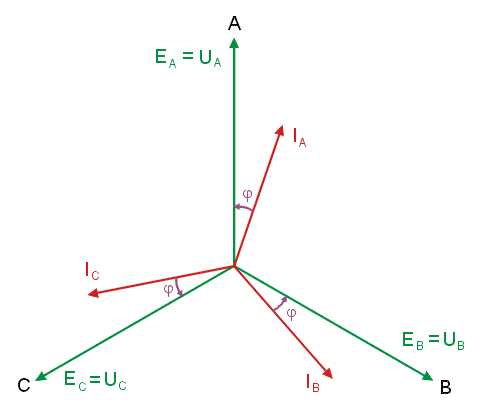
|valign="top"|Układ napięć trójfazowych odbiornika tworzą napięcia na poszczególnych jego fazach, czyli <math>U_A</math>, <math>U_B</math>, <math>U_C</math>. W efekcie w obwodzie trójfazowym o połączeniu gwiazda-gwiazda wyróżnia się dwa układy napięć trójfazowych gwiazdowych: generatora <math>E_A</math>, <math>E_B</math>, <math>E_C</math> i odbiornika <math>U_A</math>, <math>U_B</math>, <math>U_C</math>. | |||
Dla obliczenia prądów w obwodzie należy wyznaczyć układ napięć odbiornikowych. Najlepiej dokonać tego wyznaczając napięcie <math>U_N</math>. Zastosujemy metodę potencjałów węzłowych przy założeniu, że punkt 0 jest węzłem odniesienia a poszukiwany potencjał węzłowy jest równy <math>U_N</math>. Zgodnie z metodą potencjałów węzłowych otrzymuje się | |||
: <math>E_AY_A+E_BY_B+E_CY_C=U_N(Y_A+Y_B+Y_C+Y_N)</math> | |||
Stąd | |||
: <math>U_N={E_AY_A+E_BY_B+E_CY_C \over (Y_A+Y_B+Y_C+Y_N)}</math> | |||
gdzie wielkości oznaczone symbolem <math>Y\,</math> są admitancjami: <math>Y_A={1 \over Z_A}</math>, <math>Y_B={1 \over Z_B}</math>, <math>Y_C={1 \over Z_C}</math> oraz <math>Y_N={1 \over Z_N}</math>. Wyznaczenie wartości napięcia <math>U_N</math> pozwala obliczyć wartości napięć odbiornikowych. Z prawa napięciowego Kirchhoffa napisanego dla trzech oczek w obwodzie wynika | |||
: <math>U_A=E_A-U_N</math> | |||
: <math>U_B=E_B-U_N</math> | |||
: <math>U_C=E_C-U_N</math> | |||
Przy znanych wartościach admitancji odbiornika obliczenie prądu polega na zastosowaniu prawa Ohma. Mianowicie | |||
: <math>I_A=Y_AU_A</math> | |||
: <math>I_B=Y_BU_B</math> | |||
: <math>I_C=Y_CU_C</math> | |||
: <math>I_N=Y_NU_N</math> | |||
Suma prądów w węźle <math>N\,</math> jest równa zeru, zatem <math>I_A+I_B+I_C=I_N</math>. Moce wydzielone w odbiorniku trójfazowym oblicza się jako sumę mocy wydzielonych w poszczególnych fazach odbiornika, czyli | |||
: <math>S_A=P_A+jQ_A=U_AI_A^*</math> | |||
: <math>S_B=P_B+jQ_B=U_BI_B^*</math> | |||
: <math>S_C=P_C+jQ_C=U_CI_C^*</math> | |||
Moc wydzielona na impedancji przewodu zerowego oznacza moc strat. Jest ona równa | |||
: <math>S_N=P_N+jQ_N=U_NI_N^*</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd12.png]] | |||
|valign="top"|Otrzymane wyniki można zinterpretować na wykresie wektorowym prądów i napięć w obwodzie. Rysunek poniżej (oraz na slajdzie nr 12) przedstawia przypadek obciążenia niesymetrycznego. | |||
[[Grafika:PEE_M6_anim_3.gif]] | |||
Widoczne są dwie gwiazdy napięć fazowych: generatora o środku w punkcie <math>0\,</math> i odbiornika o środku w punkcie <math>N\,</math>. Dla obu gwiazd obowiązuje jeden trójkąt napięć międzyfazowych. Przesunięcie potencjału punktu <math>N\,</math> względem <math>0\,</math> (napięcie <math>U_N</math> różne od zera) jest spowodowane niesymetrią odbiornika. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd13.png]] | |||
|valign="top"|W pracy układu trójfazowego gwiazdowego można wyróżnić kilka szczególnych przypadków. | |||
* '''Odbiornik symetryczny''' (<math>Z_A=Z_B=Z_C=Z</math>) z dowolną wartością impedancji przewodu zerowego | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd14.png]] | |||
|valign="top"|W tym przypadku napięcie niezrównoważenia <math>U_N=0</math>, a prąd przewodu zerowego <math>I_N=0</math>. Wszystkie prądy fazowe są równe co do amplitydy i przesunięte w fazie o <math>120^\circ</math>. Rysunek poniżej (oraz na slajdzie nr 14) przedstawia wykres wektorowy prądów i napięć dla tego przypadku. | |||
[[Grafika:PEE_M6_anim_4.gif]] | |||
Odbiornik symetryczny jest jednym z częściej występujących przypadków w praktyce. Przykładami takich odbiorników są: silniki elektryczne trójfazowe czy piece grzejne trójfazowe (zwykle o dużej mocy). | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd15.png]] | |||
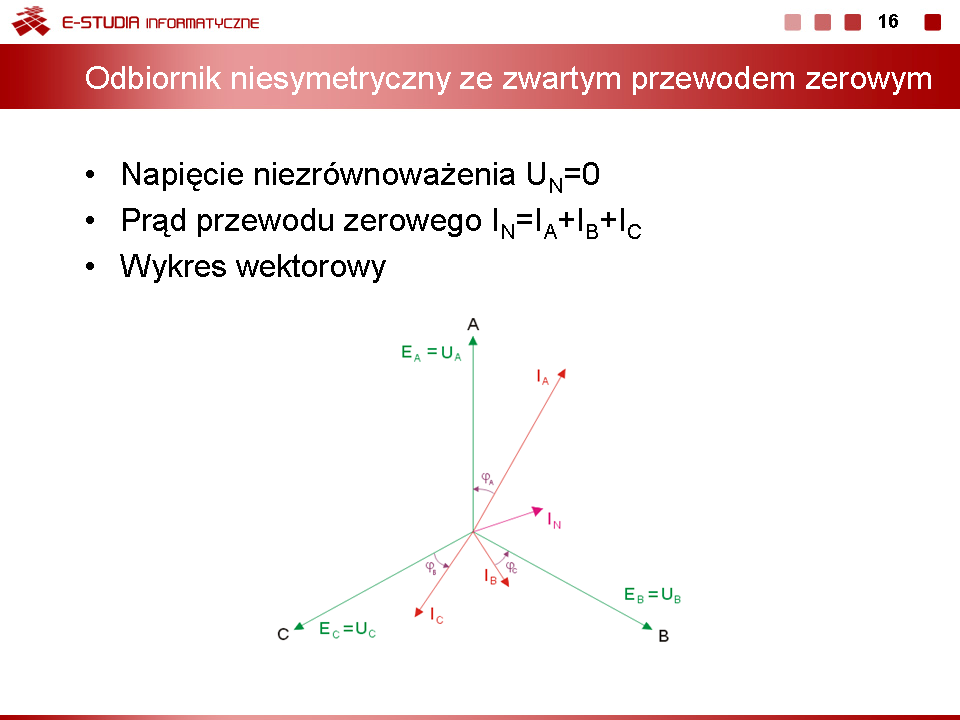
|valign="top"|* Odbiornik niesymetryczny przy zwartym przewodzie zerowym | |||
W tym przypadku napięcie niezrównoważenia <math>U_N=0</math>, a prąd przewodu zerowego <math>I_N \neq 0</math>. Prądy fazowe są wówczas określane bezpośrednio na podstawie układu napięć generatorowych. Suma tych prądów w ogólnym przypadku odbiornika niesymetrycznego jest różna od zera | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd16.png]] | |||
|valign="top"| | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd17.png]] | |||
|valign="top"| | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd18.png]] | |||
|valign="top"| | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd19.png]] | |||
|valign="top"| | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd20.png]] | |||
|valign="top"| | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M6_Slajd21.png]] | |||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 152: | Linia 270: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd22.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 159: | Linia 277: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M6_Slajd23.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
Wersja z 10:36, 1 sie 2006

|
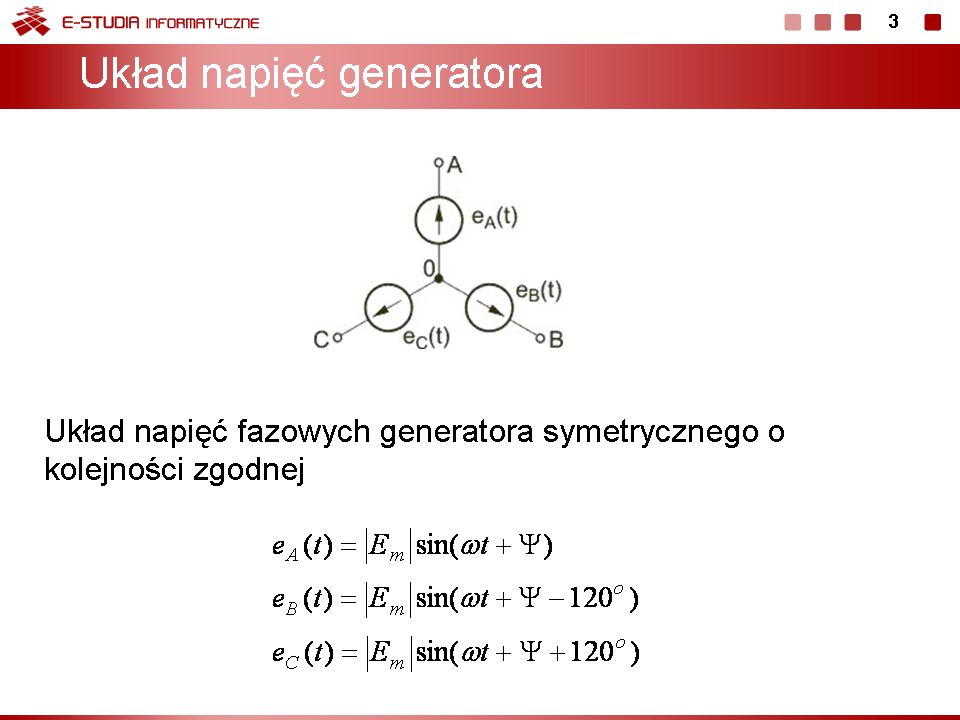
Wykład 6. Układy trójfazowe |

|
W pracy układu trójfazowego gwiazdowego można wyróżnić kilka szczególnych przypadków.
|

|

|

|

|

|
|

|

|