Matematyka dyskretna 1/Test 14: Grafy III: Różnice pomiędzy wersjami

Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
← poprzednia edycjanastępna edycja →
WizualnieWikikod
m Zastępowanie tekstu - "<div class="thumb t(.*)"><div style="width:(.*)px;"> <flash>file=(.*)\.swf\|width=(.*)\|height=(.*)<\/flash> <div\.thumbcaption>(.*)<\/div><\/div> <\/div>" na "$4x$5px|thumb|$1|$6"
m Zastępowanie tekstu – „\displaystyle ” na „”
Linia 10: Linia 10:
</quiz>  
</quiz>  


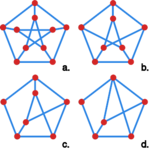
<quiz>Który z grafów przedstawionych na Rysunku 2 jest homeomorficzny z kliką  <math>\displaystyle \mathcal{K}_{5} </math> ?
<quiz>Który z grafów przedstawionych na Rysunku 2 jest homeomorficzny z kliką  <math>\mathcal{K}_{5} </math> ?


<wrongoption>graf przedstawiony na rysunku 2.a.</wrongoption>
<wrongoption>graf przedstawiony na rysunku 2.a.</wrongoption>
Linia 19: Linia 19:




<quiz>Spójny graf planarny o  <math>\displaystyle 20 </math>  wierzchołkach, z których każdy jest stopnia  <math>\displaystyle 3 </math>  ma:
<quiz>Spójny graf planarny o  <math>20 </math>  wierzchołkach, z których każdy jest stopnia  <math>3 </math>  ma:
<wrongoption> <math>\displaystyle 11 </math>  ścian</wrongoption>
<wrongoption> <math>11 </math>  ścian</wrongoption>
<rightoption> <math>\displaystyle 12 </math>  ścian</rightoption>
<rightoption> <math>12 </math>  ścian</rightoption>
<wrongoption> <math>\displaystyle 22 </math>  ścian</wrongoption>
<wrongoption> <math>22 </math>  ścian</wrongoption>
<wrongoption> <math>\displaystyle 24 </math>  ścian</wrongoption>
<wrongoption> <math>24 </math>  ścian</wrongoption>
</quiz>  
</quiz>  




<quiz>Ile spójnych składowych ma graf planarny o <math>\displaystyle 121 </math>  wierzchołkach, <math>\displaystyle 53 </math> krawędziach, oraz  <math>\displaystyle 30 </math>  ścianach?
<quiz>Ile spójnych składowych ma graf planarny o <math>121 </math>  wierzchołkach, <math>53 </math> krawędziach, oraz  <math>30 </math>  ścianach?
<rightoption> <math>\displaystyle 98 </math> </rightoption>
<rightoption> <math>98 </math> </rightoption>
<wrongoption> <math>\displaystyle 99 </math> </wrongoption>
<wrongoption> <math>99 </math> </wrongoption>
<wrongoption> <math>\displaystyle 100 </math> </wrongoption>
<wrongoption> <math>100 </math> </wrongoption>
<wrongoption> <math>\displaystyle 143 </math> </wrongoption>
<wrongoption> <math>143 </math> </wrongoption>
</quiz>  
</quiz>  




<quiz>Niech  <math>\displaystyle \mathbf{G}^* </math>  będzie grafem geometrycznie dualnym do  
<quiz>Niech  <math>\mathbf{G}^* </math>  będzie grafem geometrycznie dualnym do  
grafu płaskiego  <math>\displaystyle \mathbf{G} </math> .
grafu płaskiego  <math>\mathbf{G} </math> .
Podzbiór  <math>\displaystyle C </math>  zbioru krawędzi grafu  <math>\displaystyle \mathbf{G} </math>  jest cyklem w grafie  <math>\displaystyle \mathbf{G} </math>   
Podzbiór  <math>C </math>  zbioru krawędzi grafu  <math>\mathbf{G} </math>  jest cyklem w grafie  <math>\mathbf{G} </math>   
wtedy i tylko wtedy, gdy zbiór krawędzi dualnych do krawędzi zbioru  <math>\displaystyle C </math>  
wtedy i tylko wtedy, gdy zbiór krawędzi dualnych do krawędzi zbioru  <math>C </math>  
<wrongoption>posiada parzystą liczbę elementów</wrongoption>
<wrongoption>posiada parzystą liczbę elementów</wrongoption>
<wrongoption>posiada nieparzystą liczbę elementów</wrongoption>
<wrongoption>posiada nieparzystą liczbę elementów</wrongoption>
<wrongoption>jest cyklem grafu  <math>\displaystyle \mathbf{G}^* </math> </wrongoption>
<wrongoption>jest cyklem grafu  <math>\mathbf{G}^* </math> </wrongoption>
<rightoption>jest rozcięciem grafu  <math>\displaystyle \mathbf{G}^* </math> </rightoption>
<rightoption>jest rozcięciem grafu  <math>\mathbf{G}^* </math> </rightoption>
</quiz>  
</quiz>  




<quiz>Spójny graf prosty, który nie jest pełny, i w którym wszystkie wierzchołki  mają stopień nie większy niż  <math>\displaystyle k </math> jest:
<quiz>Spójny graf prosty, który nie jest pełny, i w którym wszystkie wierzchołki  mają stopień nie większy niż  <math>k </math> jest:
<wrongoption> <math>\displaystyle \left( k-1 \right) </math> -kolorowalny</wrongoption>
<wrongoption> <math>\left( k-1 \right) </math> -kolorowalny</wrongoption>
<rightoption> <math>\displaystyle k </math> -kolorowalny</rightoption>
<rightoption> <math>k </math> -kolorowalny</rightoption>
<rightoption> <math>\displaystyle \left( k+1 \right) </math> -kolorowalny</rightoption>
<rightoption> <math>\left( k+1 \right) </math> -kolorowalny</rightoption>
<rightoption> <math>\displaystyle 2k </math> -kolorowalny</rightoption>
<rightoption> <math>2k </math> -kolorowalny</rightoption>
</quiz>  
</quiz>  




<quiz>Iloma kolorami można pokolorować polityczną mapę Europy?
<quiz>Iloma kolorami można pokolorować polityczną mapę Europy?
<wrongoption> <math>\displaystyle 3 </math> </wrongoption>
<wrongoption> <math>3 </math> </wrongoption>
<rightoption> <math>\displaystyle 4 </math> </rightoption>
<rightoption> <math>4 </math> </rightoption>
<rightoption> <math>\displaystyle 5 </math> </rightoption>
<rightoption> <math>5 </math> </rightoption>
<rightoption> <math>\displaystyle 6 </math> </rightoption>
<rightoption> <math>6 </math> </rightoption>
</quiz>  
</quiz>  




<quiz>W grafie prostym zachodzi:
<quiz>W grafie prostym zachodzi:
<rightoption> <math>\displaystyle \chi\!\left( \mathbf{G} \right)\leq\chi_s\!\left( \mathbf{G} \right)+1 </math> </rightoption>
<rightoption> <math>\chi\!\left( \mathbf{G} \right)\leq\chi_s\!\left( \mathbf{G} \right)+1 </math> </rightoption>
<wrongoption> <math>\displaystyle \chi\!\left( \mathbf{G} \right)\leq\chi_s\!\left( \mathbf{G} \right) </math> </wrongoption>
<wrongoption> <math>\chi\!\left( \mathbf{G} \right)\leq\chi_s\!\left( \mathbf{G} \right) </math> </wrongoption>
<wrongoption> <math>\displaystyle \chi\!\left( \mathbf{G} \right)\geq\chi_s\!\left( \mathbf{G} \right)+1 </math> </wrongoption>
<wrongoption> <math>\chi\!\left( \mathbf{G} \right)\geq\chi_s\!\left( \mathbf{G} \right)+1 </math> </wrongoption>
<wrongoption> <math>\displaystyle \chi\!\left( \mathbf{G} \right)=\chi_s\!\left( \mathbf{G} \right) </math> </wrongoption>
<wrongoption> <math>\chi\!\left( \mathbf{G} \right)=\chi_s\!\left( \mathbf{G} \right) </math> </wrongoption>
</quiz>  
</quiz>  




<quiz>Pełny graf dwudzielny <math>\displaystyle K_{50,50}</math>:
<quiz>Pełny graf dwudzielny <math>K_{50,50}</math>:
<rightoption> jest grafem Hamiltonowskim</rightoption>
<rightoption> jest grafem Hamiltonowskim</rightoption>
<rightoption> jest grafem Eulerowskim</rightoption>
<rightoption> jest grafem Eulerowskim</rightoption>

Wersja z 08:49, 28 sie 2023

Rysunek 1
Rysunek 2

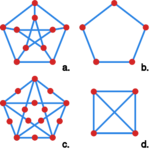
Który z grafów przedstawionych na Rysunku 1 jest planarny?

graf przedstawiony na rysunku 1.a.

graf przedstawiony na rysunku 1.b.

graf przedstawiony na rysunku 1.c.

graf przedstawiony na rysunku 1.d.

Który z grafów przedstawionych na Rysunku 2 jest homeomorficzny z kliką 𝒦5 ?

graf przedstawiony na rysunku 2.a.

graf przedstawiony na rysunku 2.b.

graf przedstawiony na rysunku 2.c.

graf przedstawiony na rysunku 2.d.


Spójny graf planarny o 20 wierzchołkach, z których każdy jest stopnia 3 ma:

11 ścian

12 ścian

22 ścian

24 ścian


Ile spójnych składowych ma graf planarny o 121 wierzchołkach, 53 krawędziach, oraz 30 ścianach?

98

99

100

143


Niech 𝐆* będzie grafem geometrycznie dualnym do grafu płaskiego 𝐆 . Podzbiór C zbioru krawędzi grafu 𝐆 jest cyklem w grafie 𝐆 wtedy i tylko wtedy, gdy zbiór krawędzi dualnych do krawędzi zbioru C

posiada parzystą liczbę elementów

posiada nieparzystą liczbę elementów

jest cyklem grafu 𝐆*

jest rozcięciem grafu 𝐆*


Spójny graf prosty, który nie jest pełny, i w którym wszystkie wierzchołki mają stopień nie większy niż k jest:

(k−1) -kolorowalny

k -kolorowalny

(k+1) -kolorowalny

2k -kolorowalny


Iloma kolorami można pokolorować polityczną mapę Europy?

3

4

5

6


W grafie prostym zachodzi:

χ(𝐆)≤χs(𝐆)+1

χ(𝐆)≤χs(𝐆)

χ(𝐆)≥χs(𝐆)+1

χ(𝐆)=χs(𝐆)


Pełny graf dwudzielny K50,50:

jest grafem Hamiltonowskim

jest grafem Eulerowskim

jest lasem

jest dwukolorowalny

jest 49-kolorowalny

Źródło: „https://wazniak.mimuw.edu.pl/index.php?title=Matematyka_dyskretna_1/Test_14:_Grafy_III&oldid=79721”