PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 188: | Linia 188: | ||
Przyjąć następujące wartości parametrów elementów obwodu: <math>R=5\Omega, L1=2H, L2=2H, M=1H</math> oraz <math>i(t)=5sin(t+45^o)A</math>. | Przyjąć następujące wartości parametrów elementów obwodu: <math>R=5\Omega, L1=2H, L2=2H, M=1H</math> oraz <math>i(t)=5sin(t+45^o)A</math>. | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd13.png]] | |||
|valign="top"|'''Rozwiązanie''' | |||
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono na rysunku | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd14.png]] | |||
|valign="top"|Wielkości symboliczne charakteryzujące elementy obwodu: | |||
<math>I=\frac{5}{\sqrt2}e^{j45^o}</math> | |||
<math>Z_1=j\omega(L_1-M)=j1</math> | |||
<math>Z_2=j\omega(L_2-M)=0</math> | |||
<math>Z_M=j\omega M=j1</math> | |||
Impedancja zastępcza obwodu wobec <math>Z_2=0</math> | |||
<math>Z=\frac{RZ_M}{R+Z_M}=\frac{1}{\sqrt2}e^{j45^o}</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd15.png]] | |||
|valign="top"|Napięcie <math>U_A_B\,</math> | |||
<math>U_{AB}=ZI=j5</math> | |||
Prądy: | |||
<math>I_R=\frac{U_{AB}}{R}=j5</math> | |||
<math>I_1=0</math> | |||
<math>I_2=I_3\frac{U_{AB}}{Z_M}=5</math> | |||
Napięcia na elementach równoległych w obwodzie oryginalnym i zastępczym są sobie równe i wynoszą <math>U_{AB}=j5</math> Można to łatwo sprawdzić w obwodzie oryginalnym obliczając napięcia na cewkach sprzężonych. Mianowicie | |||
<math>U_{L_1}=j\omega L_1I_1+j\omega MI_2=j5</math> | |||
<math>U_{L_2}=j\omega L_2I_2+j\omega MI_1=j5</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd16.png]] | |||
|valign="top"|'''Transformator ''' | |||
'''Podstawy fizyczne działania transformatora''' | |||
Transformator jest układem przetwarzającym napięcie wejściowe w napięcie wyjściowe za pośrednictwem strumienia magnetycznego przy braku bezpośredniego połączenia galwanicznego między obu zaciskami (wejściowymi i wyjściowymi). Transformatory mogą być stosowane do różnych celów, ale podstawowym ich zadaniem jest zmiana wartości napięcia wejściowego na inną wartość napięcia wyjściowego. Może to być zarówno podwyższenie jak i obniżenie wartości. Przy zmianie napięcia ulegają odpowiedniej zmianie również prądy w uzwojeniach transformatora. | |||
W analizie teoretycznej przyjmować będziemy transformator idealizowany, czyli taki w którym nie ma strat energii, nie istnieje zjawisko rozpraszania strumienia magnetycznego (współczynnik sprzężenia magnetycznego k=1), nie występują efekty pasożytnicze (np. pojemności międzyzwojowe), nie uwzględniona jest rezystancja uzwojeń, zjawiska prądów wirowych itp. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd1.png]] | |||
|valign="top"|Przekazywanie energii elektrycznej z jednego obwodu do drugiego następuje za pośrednictwem pola elektromagnetycznego (strumienia magnetycznego). Na rysunku przedstawiono poglądowy schemat transformatora zasilanego napięciem <math>U_1\,</math> i obciążonego po stronie wtórnej impedancją <math>Z_o\,</math>. | |||
Uzwojenie, do którego jest zazwyczaj doprowadzone źródło energii elektrycznej, nazywamy uzwojeniem pierwotnym, natomiast uzwojenie, do którego jest dołączony odbiornik, nazywamy uzwojeniem wtórnym. Zaciski uzwojenia pierwotnego stanowią wejście układu, a zaciski uzwojenia wtórnego - wyjście. Odpowiednie napięcia i prądy w transformatorze nazywamy pierwotnymi lub wtórnymi. Wszystkie wielkości i parametry związane z uzwojeniem pierwotnym opatrzymy wskaźnikiem 1, a wielkości i parametry związane z uzwojeniem wtórnym – wskaźnikiem 2. | |||
Do uzwojenia pierwotnego przyłożone jest napięcie sinusoidalnie zmienne o wartości chwilowej <math>u_1(t)\,</math>. Wartość chwilową prądu w uzwojeniu pierwotnym oznaczymy przez <math>i_1(t)\,</math> Pod wpływem zmiennego w czasie prądu <math>i_1(t)\,</math> w przestrzeni otaczającej uzwojenie powstaje zmienny strumień magnetyczny <math>\phi\,</math> , będący superpozycją strumieni i . Przy założeniu jego równomiernego rozkładu na przekroju S, strumień jest iloczynem indukcji magnetycznej B i przekroju S, . Strumień ten kojarzy się zarówno z uzwojeniem pierwotnym o liczbie zwojów z1 wytwarzając strumień skojarzony , jak i uzwojeniem wtórnym o liczbie zwojów z2 wytwarzając w nim strumień skojarzony . Zgodne z prawem indukcji elektromagnetycznej pod wpływem zmiennego w czasie strumienia magnetycznego indukuje się napięcie u(t) | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 10:01, 1 sie 2006

|
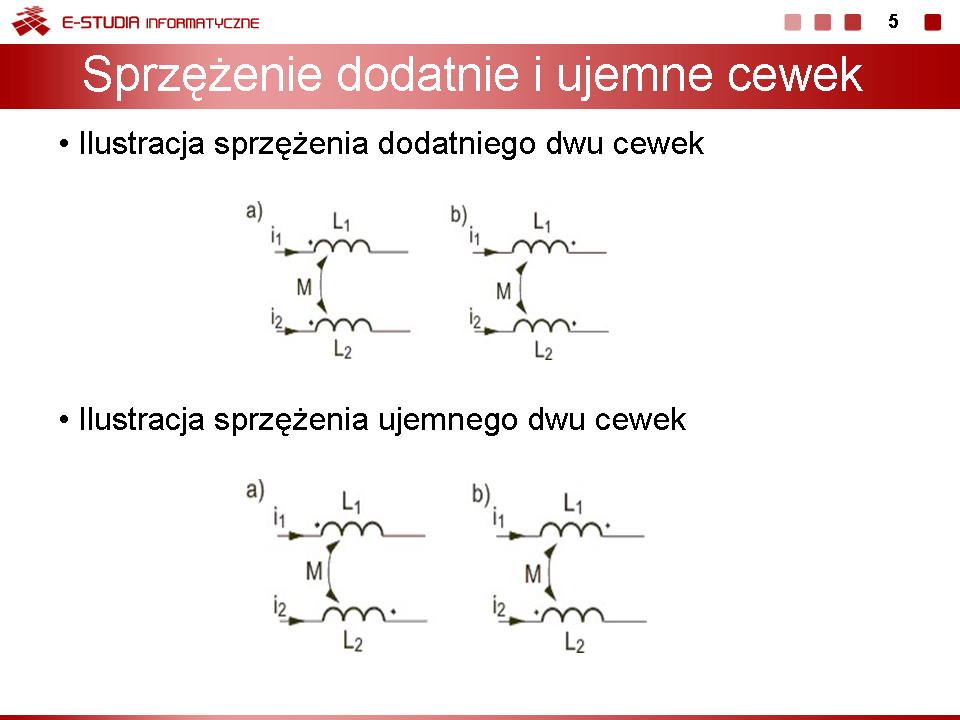
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
|
|
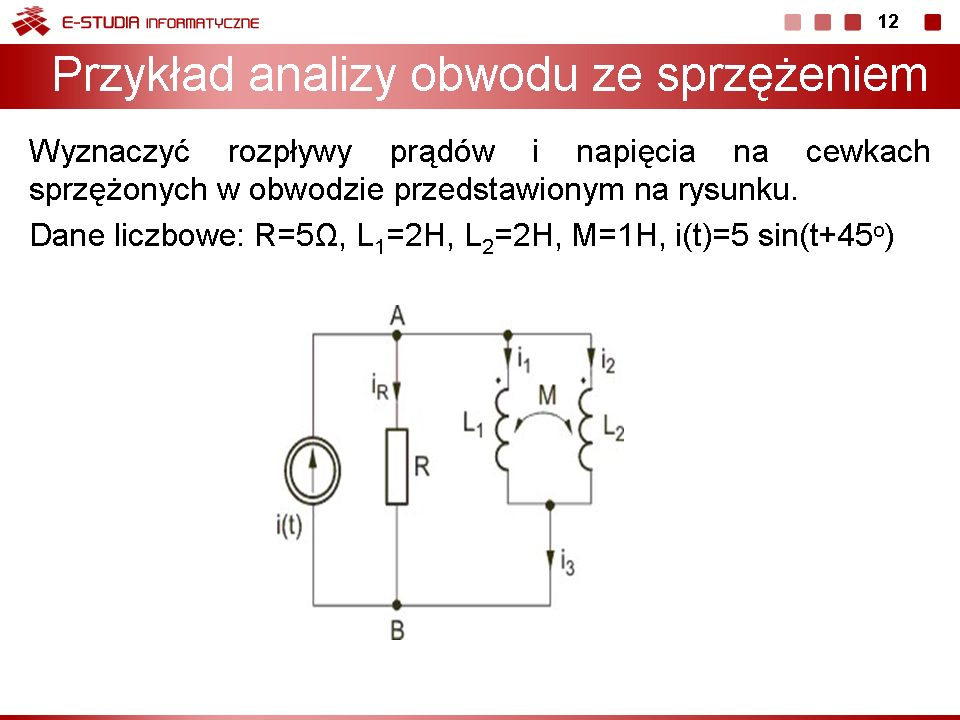
PRZYKŁAD
Wyznaczyć rozpływy prądów w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Rozwiązanie
Postać obwodu po eliminacji sprzężenia magnetycznego przedstawiono na rysunku |

|
Wielkości symboliczne charakteryzujące elementy obwodu:
Impedancja zastępcza obwodu wobec
|