PEE Moduł 5

Wykład 5. Obwody ze sprzężeniami magnetycznymi

---

Zjawiska fizyczne przy sprzężeniu magnetycznym cewek Przyjmijmy, że dwie cewki są położone blisko siebie w taki sposób, że strumień magnetyczny jednej cewki przenika również drugą. Całkowity strumień skojarzony z daną cewką (strumień skojarzony jest sumą strumieni $\varphi$ każdego zwoju cewki, co przy z zwojach o identycznym strumieniu daje $\psi =z\varphi$ jest wtedy sumą obu strumieni, jeśli ich kierunki są zgodne lub ich różnicą, jeśli kierunki strumieni są przeciwne. Strumienie obu cewek zapiszemy wówczas w postaci. ${\psi }_1={\psi }_1{}_1\pm {\psi }_1{}_2$ ${\psi }_2={\psi }_2{}_2\pm {\psi }_2{}_1$

---

Strumień ${\psi }_1{}_1$ występujący w cewce pierwszej pochodzi od prądu tej cewki a strumień jest wytworzony przez cewkę drugą i przenika przez cewkę pierwszą. Podobnie strumień ${\psi }_2{}_2$ pojawiający się w cewce drugiej pochodzi od prądu tej cewki a strumień pochodzący od prądu cewki pierwszej przenika przez cewkę drugą. Uwzględniając pojęcie indukcyjności własnej i wzajemnej wprowadzone w rozdziale pierwszym dla cewek liniowych sprzężonych magnetycznie obowiązują następujące relacje: Indukcyjności własne $L_1=\frac{{\psi }_1{}_1}{i_1}$ $L_2=\frac{{\psi }_2{}_2}{i_2}$ Indukcyjności wzajemne $M_1{}_2=\frac{{\psi }_1{}_2}{i_2}$ $M_2{}_{=}\frac{{\psi }_2{}_1}{i_1}$ Dla środowisk o tej samej przenikalności magnetycznej obie indukcyjności wzajemne są sobie równe, to znaczy $M_1{}_2=M_2{}_1=M$ Dla dwu cewek sprzężonych magnetycznie definiuje się współczynnik sprzężenia jako średnią geometryczną współczynników sprzężenia obu cewek, przy czym współczynnik sprzężenia jednej cewki z drugą jest określany jako stosunek strumienia głównego cewki pochodzącego od prądu własnego do strumienia całkowitego cewki. Współczynnik sprzężenia cewek oznaczać będziemy literą $k$. Spełnia on następującą relację $M=k\sqrt{L_1{L}_2}$ Przy idealnym (pełnym) sprzężeniu cewek wartość współczynnika sprzężenia jest równa jeden (k=1). Indukcyjność wzajemna jest wówczas średnią geometryczną indukcyjności własnych obu cewek. Przy braku sprzężenia magnetycznego między cewkami wartość k=0.

---

Sprzężenie magnetyczne powoduje indukowanie się napięcia w cewce od zmian prądu własnego cewki i od zmian prądu cewki z nią sprzężonej. Wzory określające odpowiednie napięcia na cewkach sprzężonych magnetycznie dane są wówczas w postaci Parser nie mógł rozpoznać (nieznana funkcja „\L”): {\displaystyle u_1=\frac{d\psi_1}{dt}\L_1\frac{di_1}{dt}\pm M\frac{di_2}{dt}} Parser nie mógł rozpoznać (nieznana funkcja „\L”): {\displaystyle u_2=\frac{d\psi_2}{dt}\L_2\frac{di_2}{dt}\pm M\frac{di_1}{dt}} Znak plus lub minus występujący we wzorze odpowiada sprzężeniu bądź dodatniemu (znak plus) bądź ujemnemu (znak minus). Rodzaj sprzężenia zależy od kierunku prądu cewki względem początku uzwojenia.

---

Zauważmy, że przy istnieniu sprzężenia magnetycznego w cewce generowane jest napięcie na cewce nawet przy prądzie własnym cewki równym zeru. Oznacza to przenoszenie się energii z jednego obwodu do drugiego drogą magnetyczną.

---

---

Analiza obwodów magnetycznie sprzężonych przy wymuszeniu sinusoidalnym Równania symboliczne elementów sprzężonych magnetycznie Analiza obwodów ze sprzężeniami magnetycznymi w stanie ustalonym przy wymuszeniu sinusoidalnym może być przeprowadzona przy zastosowaniu metody symbolicznej, w której w miejsce różniczkowania wprowadza się działania na liczbach zespolonych. Dla wymuszenia sinusoidalnego wzory różniczkowe upraszczają się do zależności algebraicznych typu zespolonego, które podobnie jak dla indukcyjności własnych wyprowadzonych w rozdziale drugim można zapisać w postaci Parser nie mógł rozpoznać (nieznana funkcja „\omeha”): {\displaystyle U_1=j\omega L_1I_1\pm j\omeha MI_2} Parser nie mógł rozpoznać (nieznana funkcja „\omeha”): {\displaystyle U_2=j\omega L_2I_2\pm j\omeha MI_1} Znak plus obowiązuje dla sprzężenia dodatniego (strumienie magnetyczne obu cewek sumują się) a znak minus dla sprzężenia ujemnego (strumienie magnetyczne obu cewek odejmują się). Jak widać z powyższych wzorów cewki sprzężone magnetycznie reprezentują sobą reaktancje, przy czym można tu wyróżnić dwa rodzaje reaktancji: reaktancję indukcyjną własną (zwaną dotąd reaktancją indukcyjną) i reaktancję indukcyjną wzajemną. Wprowadźmy następujące oznaczenia $X_M=\omega M$ reaktancja indukcyjna wzajemna $Z_M=j\omega M$ impedancja indukcyjna wzajemna

---

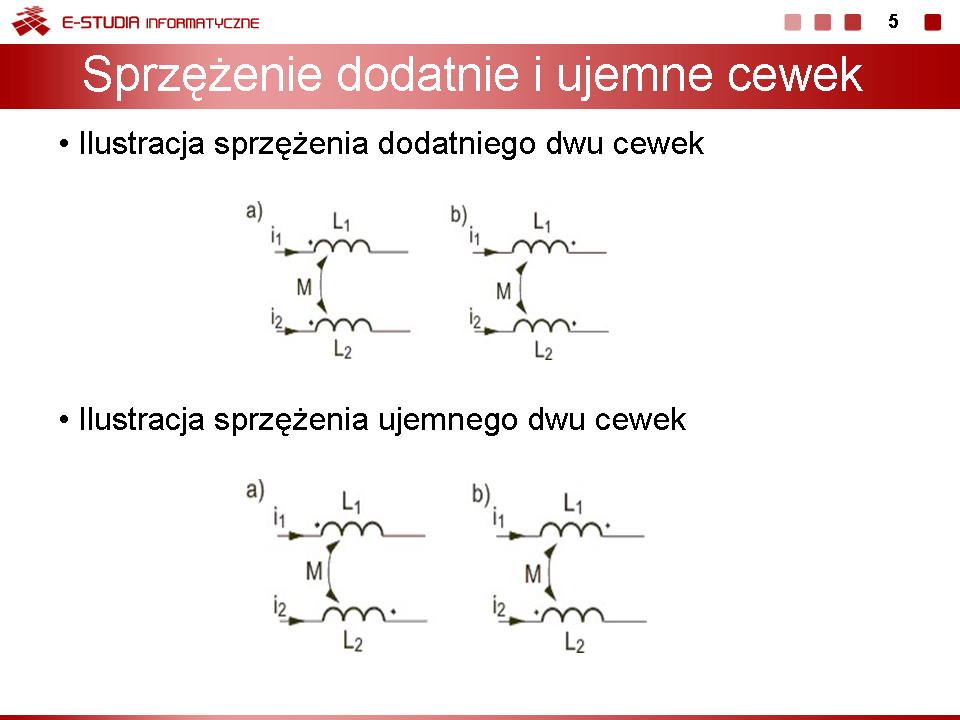
Napięcie skuteczne zespolone na cewkach sprzężonych można wówczas opisać następującymi wzorami $U_1=Z_{L1}{I}_1\pm Z_M{I}_2=j\omega L_1{I}_1\pm j\omega M{I}_2$ $U_2=Z_{L1}{I}_2\pm Z_M{I}_1=j\omega L_2{I}_2\pm j\omega M{I}_1$ w których $Z_{L1}$ oraz $Z_{L2}$ oznaczają impedancje indukcyjności własnych cewki pierwszej i drugiej, $Z_{L1}=j\omega L_1,Z_{L2}=j\omega L_2$ , . Dla wyznaczenia wartości skutecznej napięcia na cewce sprzężonej muszą być znane zarówno wartości skuteczne prądu jednej cewki jak i drugiej, sprzężonej z nią. Znak sprzężenia (plus lub minus) powoduje odejmowanie (sprzężenie ujemne) lub dodawanie (sprzężenie dodatnie) napięć pochodzących od sprzężenia.

---

Najważniejszym elementem analizy obwodów ze sprzężeniami magnetycznymi jest wyznaczenie prądów poszczególnych gałęzi w obwodzie. 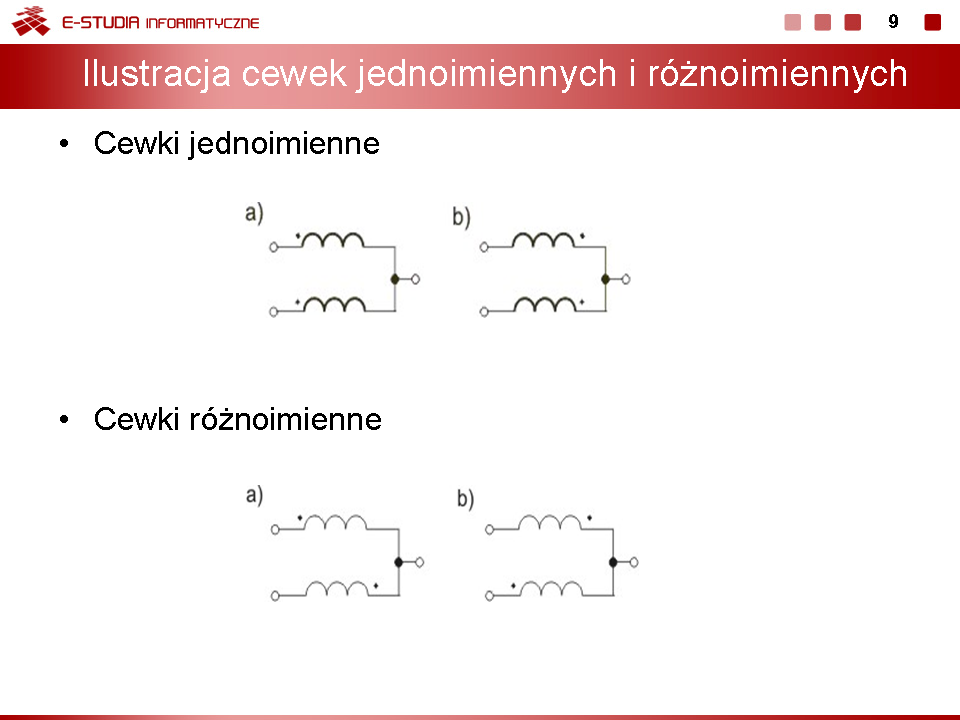Bezpośrednie zastosowanie poznanych dotąd metod analizy obwodów (metoda węzłowa, oczkowa, Thevenina czy Nortona) wymaga w pierwszej kolejności wyeliminowania sprzężenia magnetycznego cewek, a więc pozbycia się wpływu prądu jednej cewki na napięcie cewki drugiej Eliminacja sprzężeń magnetycznych Eliminacja sprzężeń magnetycznych jest możliwa bezpośrednio na podstawie analizy struktury obwodu i uwzględnienia położenia początków uzwojeń cewek względem węzłów wspólnych (lub uznanych za wspólne przy braku ich bezpośredniego połączenia). W tym przypadku można wyróżnić dwa rodzaje połączeń: dwie cewki sprzężone magnetycznie mają jednakowo usytuowane początki uzwojeń względem węzła - takie cewki uważać będziemy za jednoimienne dwie cewki sprzężone magnetycznie mają przeciwnie usytuowane początki uzwojeń względem węzła - takie cewki uważać będziemy za różnoimienne.

---

Wykład 5. Obwody ze sprzężeniami magnetycznymi

---