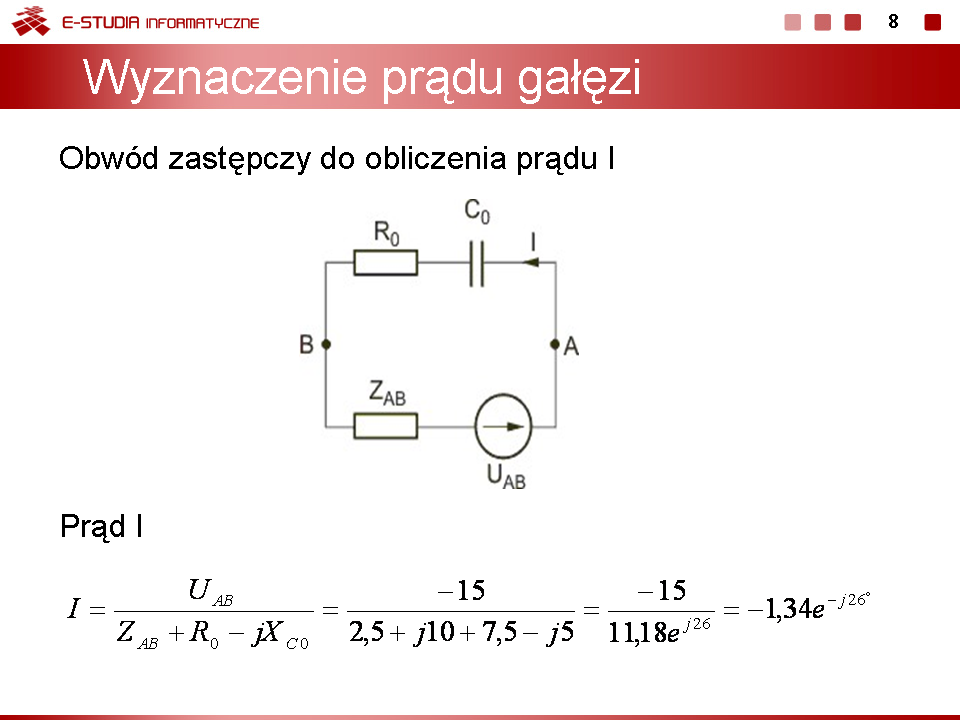
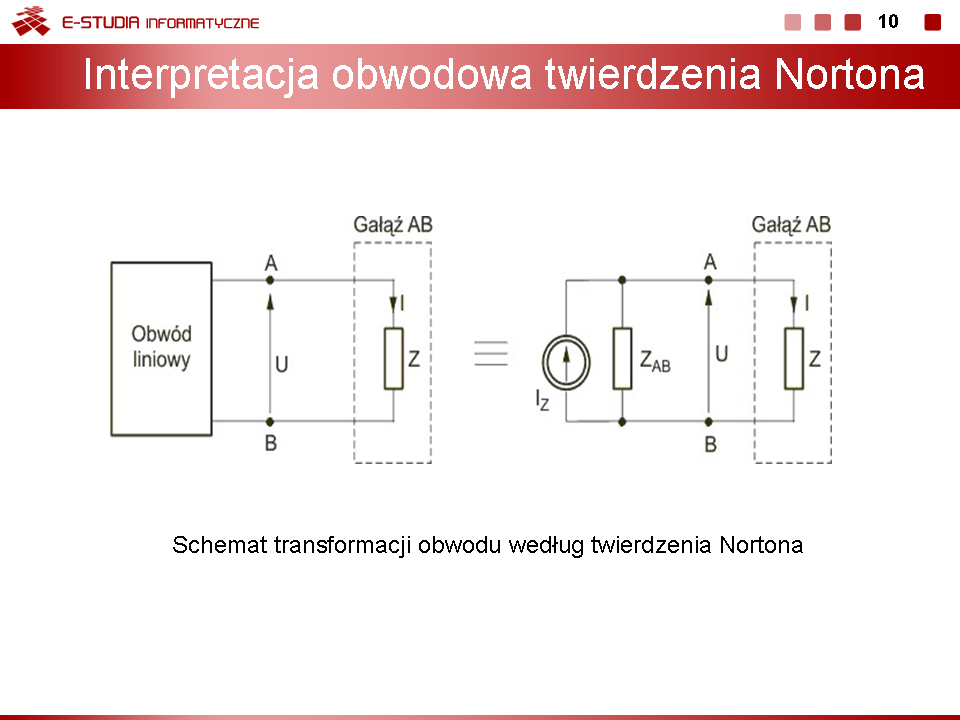
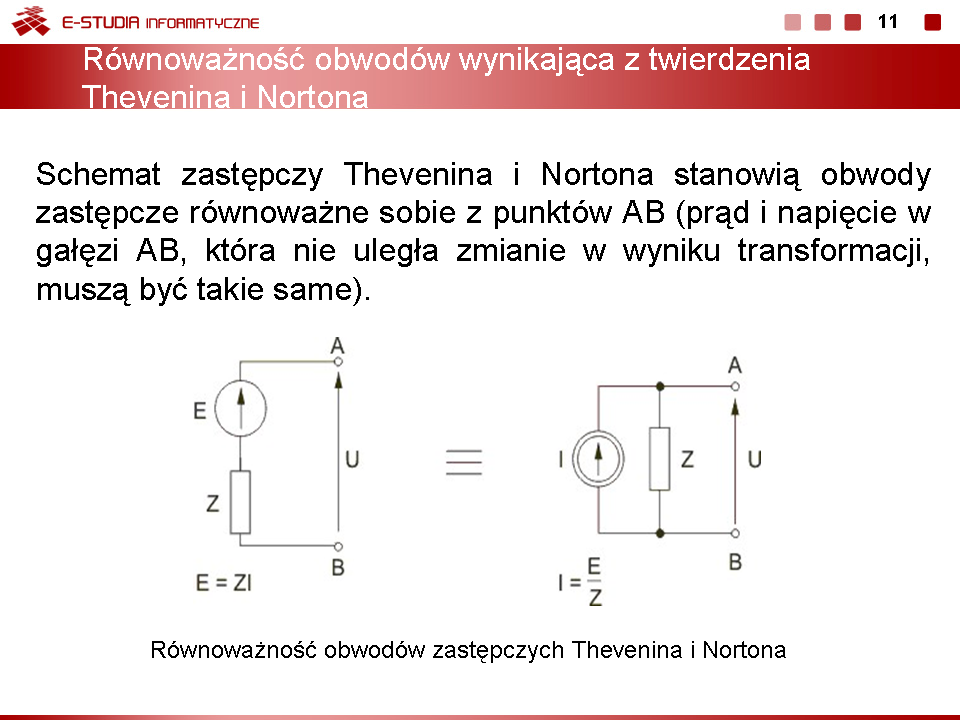
PEE Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 343: | Linia 343: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd22.png]] | ||
|valign="top"| | |valign="top"|Elementy <math>Z_{ii}</math> położone na głównej diagonalnej macierzy <math>Z\,</math> nazywamy '''impedancjami własnymi''' oczka <math>i\,</math>-tego. Przy założeniu, że wszystkie prądy oczkowe mają identyczny zwrot, dla obwodów RLC bez źródeł sterowanych impedancja własna oczka <math>i\,</math>-tego jest równa sumie impedancji wszystkich gałęzi występujących w oczku. Elementy <math>Z_{ij}</math> położone poza główną diagonalną są '''impedancjami wzajemnymi''' między oczkiem <math>i\,</math>-tym oraz <math>j\,</math>-tym. Impedancja wzajemna dwu oczek przy identycznym zwrocie wszystkich prądów oczkowych jest równa impedancji wspólnej dla obu oczek wziętej ze znakiem minus. Impedancja wzajemna oczka <math>i\,</math>-tego oraz <math>j\,</math>-tego jest taka sama jak oczka <math>j\,</math>-tego oraz <math>i\,</math>-tego, tzn. <math>Z_{ij}=Z_{ji}</math>. Macierz <math>Z\,</math> jest więc macierzą symetryczną. | ||
Element <math>k\,</math>-ty wektora wymuszeń napięciowych <math>E\,</math> jest równy sumie wszystkich napięć źródłowych występujących w <math>k\,</math>-tym oczku. Przy założonej orientacji oczka napięcie źródłowe dodaje się ze znakiem plus jeśli jego zwrot jest identyczny z tą orientacją a ze znakiem minus jeśli ten zwrot jest przeciwny. Sposób tworzenia opisu oczkowego zilustrujemy na przykładzie obwodu z rysunku na slajdzie nr 24. | |||
|} | |} | ||
| Linia 357: | Linia 360: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd24.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd24.png]] | ||
|valign="top"|''Przykład'' | |||
Dla obwodu przedstawionego na rysunku napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd25.png]] | |||
|valign="top"|Obwód zawiera 3 oczka niezależne, stąd wymiar macierzy oczkowej jest równy 3, podobnie jak liczba nieznanych składników wektora prądów oczkowych oraz liczba znanych składników wektora napięć wymuszających. Korzystając z podanej wcześniej reguły tworzenia opisu oczkowego otrzymuje się | |||
: <math>Z= | |||
\begin{bmatrix} | |||
Z_1+Z_2+Z_3 & -Z_3 & -Z_1\\ | |||
-Z_3 & Z_3+Z_4+Z_5 & -Z_5\\ | |||
-Z_1 & -Z_5 & Z_1+Z_5+Z_6 | |||
\end{bmatrix}</math> | |||
: <math>E= | |||
\begin{bmatrix} | |||
-E_1-E_3\\ | |||
E_3+E_4\\ | |||
E_1-E_6 | |||
\end{bmatrix}</math> | |||
Biorąc pod uwagę że obwód zawiera trzy nieznane prądy oczkowe tworzące wektor prądów <math>I_0= \left [ I_{01} \ I_{02} \ I_{03} \right ] ^T</math>, równanie oczkowe <math>ZI_0=E</math> stanowi zbiór trzech równań liniowych. Rozwiązanie tego układu równań pozwala określić te zmienne. Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd26.png]] | |||
|valign="top"|<math> | |||
I_1=I_{03}-I_{01} | |||
I_2=I_{01} | |||
I_3=I_{01}-I_{02} | |||
I_4=I_{02} | |||
I_5=I_{03}-I_{02} | |||
I_6=-I_{03} | |||
</math> | |||
Metoda prądów oczkowych wymaga rozwiązania układu <math>N\,</math> równań, gdzie <math>N\,</math> oznacza liczbę oczek niezależnych. Podobnie jak w metodzie węzłowej liczba oczek jest zwykle dużo mniejsza niż liczba gałęzi obwodu, stąd metoda prądów oczkowych jest dużo bardziej efektywna niż metoda klasyczna wykorzystująca bezpośrednio prawa Kirchhoffa. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd27.png]] | |||
|valign="top"| | |valign="top"| | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd28.png]] | |||
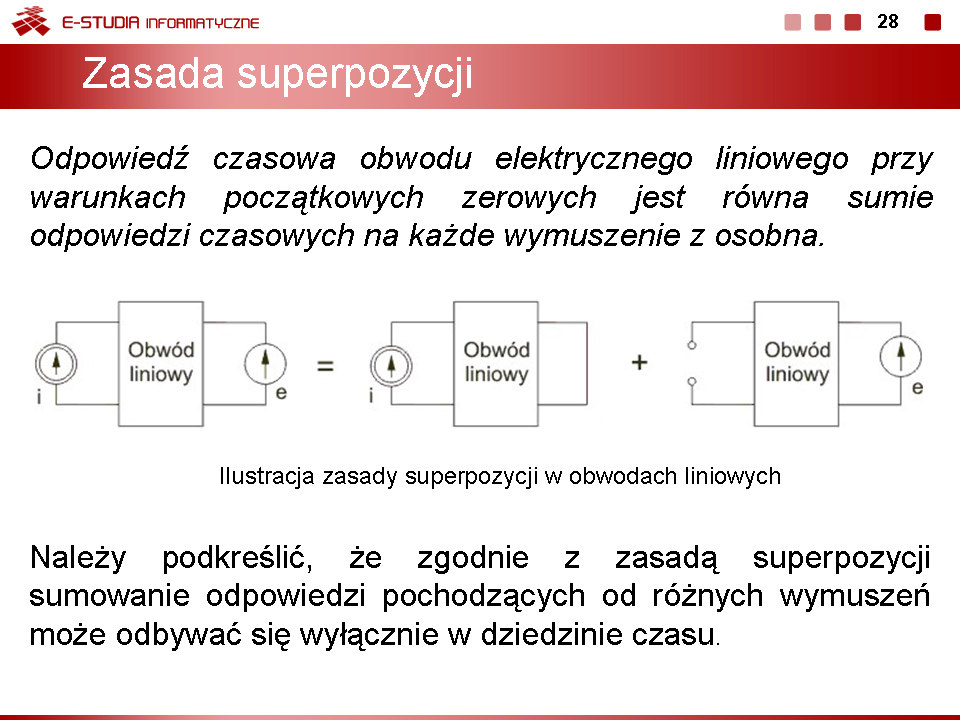
|valign="top"|'''Zasada superpozycji''' | |||
Omówione wcześniej metody analizy symbolicznej stanowią dobry i skuteczny sposób rozwiązania problemu przy istnieniu w obwodzie źródeł sinusoidalnych o tej samej częstotliwości, gdyż dla każdego źródła elementy reaktancyjne LC przedstawiają sobą te same wartości reaktancji. Istotna trudność występuje dopiero przy istnieniu w obwodzie wielu źródeł o różnych częstotliwościach. W takim przypadku nie istnieje pojęcie impedancji wspólnej dla każdego źródła, co uniemożliwia zastosowanie metody symbolicznej. Jedynym rozwiązaniem pozostaje wtedy zastosowanie zasady '''superpozycji'''. Obowiązuje ona '''tylko''' dla obwodów liniowych. Jej treść jest następująca. | |||
''Zasada superpozycji | |||
Odpowiedź czasowa obwodu elektrycznego liniowego przy warunkach początkowych zerowych jest równa sumie odpowiedzi czasowych na każde wymuszenie z osobna.'' | |||
Tak ogólnie sformułowana zasada obowiązuje zarówno w stanie ustalonym jak i nieustalonym obwodu. W przypadku analizy stanów ustalonych jej zastosowanie w analizie obwodów polega na rozbiciu danego obwodu o wielu wymuszeniach na wiele obwodów zawierających po jednym wymuszeniu, rozwiązaniu każdego z nich oddzielnie a następnie zsumowaniu odpowiedzi czasowych każdego obwodu. Należy pamiętać przy tym o zasadzie, że eliminowane źródła są zastępowane zwarciem (jeśli źródło jest napięciowe) lub rozwarciem (gdy źródło jest prądowe). | |||
Należy podkreślić, że zgodnie z zasadą superpozycji sumowanie odpowiedzi pochodzących od różnych wymuszeń może odbywać się wyłącznie w dziedzinie czasu. Sumowanie wartości zespolonych od poszczególnych wymuszeń byłoby poważnym błędem, gdyż sugerowałoby istnienie rozwiązania obwodu zawierającego tylko jedną harmoniczną. Ilustrację stosowania zasady superpozycji w analizie obwodów przedstawiono na rysunku obok (slajd 28). | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top"|'''Zadania sprawdzające''' | |||
''Zadanie 4.1'' | |||
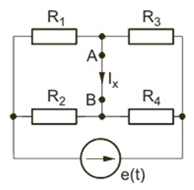
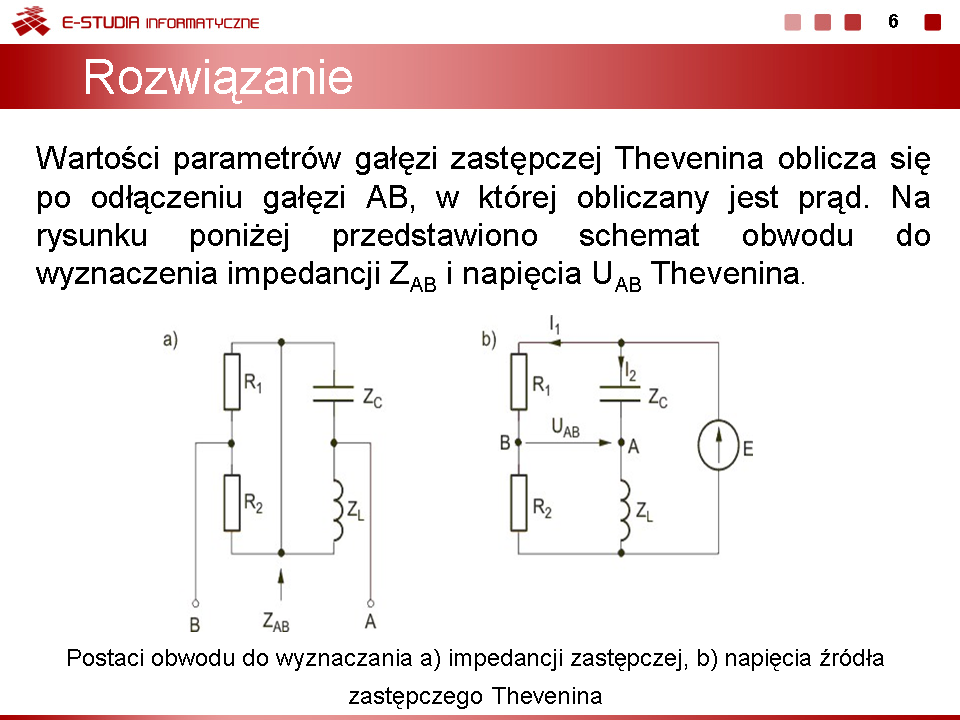
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: <math>R_1=4\Omega</math>, <math>R_2=8\Omega</math>, <math>R_3=2\Omega</math>, <math>R_4=2\Omega</math>, <math>e(t)=30\sqrt{2}sin\omega t \ V</math>. | |||
[[Grafika:PEE_M4_zadanie_4_1.png]] | |||
''Rozwiązanie'' | |||
Impedancja z zacisków AB obwodu jest równa | |||
[[Grafika:PEE_M4_zadanie_4_1_a.png]] | |||
<math>Z_{AB}={R_1R_3 \over R_1+R_3}+{R_2R_4 \over R_2+R_4}=2,93</math> | |||
Prądy w obwodzie z rys. b: | |||
<math>I_1={E \over R_1+R_3}={30 \over 6}=5</math> | |||
<math>I_2={E \over R_2+R_4}={30 \over 10}=3</math> | |||
Napięcie <math>U_{AB}</math> | |||
<math>U_{AB}=R_2I_2-R_1I_1=4</math> | |||
Poszukiwany prąd <math>I_x</math> z obwodu zastępczego Thevenina (rys. c) | |||
<math>I_x={U_{AB} \over Z_{AB}}=1,36A</math> | |||
''Zadanie 4.2'' | |||
Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. | |||
[[Grafika:PEE_M4_zadanie_4_2.png]] | |||
''Rozwiązanie'' | |||
Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci | |||
<math> | |||
\begin{bmatrix} | |||
Y_1+Y_2 & -Y_2 & 0\\ | |||
-Y_2 & Y_2+Y_3 & -Y_3+g\\ | |||
0 & -Y_3 & Y_3+Y_4 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
V_1\\ | |||
V_2\\ | |||
V_3 | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
Y_1E_1-I_1\\ | |||
0\\ | |||
-I_2 | |||
\end{bmatrix} | |||
</math> | |||
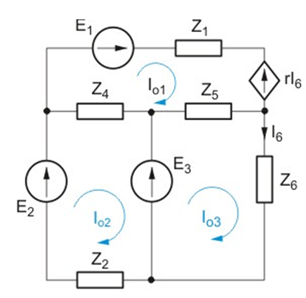
''Zadanie 4.3'' | |||
Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: | |||
[[Grafika:PEE_M4_zadanie_4_3.png]] | |||
''Rozwiązanie'' | |||
Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci | |||
: <math> | |||
\begin{bmatrix} | |||
Z_1+Z_4+Z_5 & -Z_4 & -Z_5+r\\ | |||
-Z_4 & Z_2+Z_4 & 0\\ | |||
-Z_5 & 0 & Z_5+Z_6 | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
I_{01}\\ | |||
I_{02}\\ | |||
I_{03} | |||
\end{bmatrix} | |||
= | |||
\begin{bmatrix} | |||
E_1\\ | |||
E_2-E_3\\ | |||
E_3 | |||
\end{bmatrix} | |||
</math> | |||
|} | |} | ||
Wersja z 13:40, 31 lip 2006

|
Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym |

|
|

|

|

|
Przykład
Dla obwodu przedstawionego na rysunku napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. |

|
| Zadania sprawdzające
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: , , , , . Rozwiązanie Impedancja z zacisków AB obwodu jest równa
Prądy w obwodzie z rys. b:
Napięcie
Poszukiwany prąd z obwodu zastępczego Thevenina (rys. c)
Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci
Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci |