PEE Moduł 4

Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym

---

Metoda równań Kirchhoffa W metodzie tej wykorzystuje się w bezpośredniej formie prawo prądowe i napięciowe Kirchhoffa uzupełnione o równania symboliczne opisujące poszczególne elementy obwodu. W efekcie zastosowania praw Kirchhoffa otrzymuje się układ równań algebraicznych o zespolonych współczynnikach. Jeśli założymy, że obwód posiada b gałęzi i n węzłów to w równaniach opisujących obwód wykorzystuje się (n-1) równań pochodzących z prawa prądowego Kirchhoffa. Pozostałe (b-n+1) równań wynika z prawa napięciowego Kirchhoffa dla (b-n+1) dowolnie wybranych oczek niezależnych w obwodzie (oczka uważa się za niezależne, jeśli równania napięciowe opisujące je są od siebie niezależne). Metoda oparta na twierdzeniu Thevenina Jednym z ważniejszych twierdzeń w teorii obwodów jest twierdzenie Thevenina. Pozwala ono zastąpić złożony obwód elektryczny o dowolnej strukturze i wartościach elementów, przez obwód prosty będący połączeniem szeregowym jednej impedancji zastępczej oraz źródła napięciowego. Umożliwia znaczne uproszczenie struktury obwodu, a w następstwie w bardzo prosty sposób wyznaczyć prąd lub napięcie jednej wybranej gałęzi obwodu.

---

Twierdzenie [Twierdzenie Thevenina] Dowolny, aktywny obwód liniowy można zastąpić od strony wybranych zacisków gałęzi AB uproszczonym obwodem równoważnym, złożonym z szeregowego połączenia jednego idealnego źródła napięcia i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się na podstawie analizy obwodu oryginalnego jako napięcie panujące na zaciskach AB po odłączeniu gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu.

---

Na rysunku obok (slajd 4) przedstawiono sposób transformacji obwodu zgodnie z twierdzeniem Thevenina ułatwiający obliczenie prądu w wybranej gałęzi AB obwodu. Prąd $I$ występujący w gałęzi AB obwodu oryginalnego jest równy prądowi $I$ w tej samej gałęzi obwodu uproszczonego. Napięcie $U_{AB}$ występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja $Z_{AB}$ jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB w której obliczamy prąd reprezentowana jest przez impedancję $Z$, prąd tej gałęzi można obliczyć korzystając z prawa napięciowego Kirchhoffa z którego wynika wyrażenie na prąd gałęzi w następującej postaci $I=\frac{U_{AB}}{Z+Z_{AB}}$ Metoda Thevenina w większości przypadków znakomicie upraszcza analizę obwodu. Jest szczególnie użyteczna w przypadkach, w których trzeba wyznaczyć tylko jeden prąd w obwodzie, gdyż można dokonać tego bez konieczności rozwiązywania układu równań algebraicznych lub przy znacznej redukcji liczby tych równań.

---

---

---

Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa $Z_{AB}=\frac{R_1{R}_2}{R_1+R_2}+\frac{Z_L{Z}_C}{Z_L+Z_C}=\frac{5\cdot 5}{5+5}+\frac{j5\cdot (-j10)}{j5-j10}=2,5+j10$ Rys. b na slajdzie nr 6 przedstawia obwód do obliczenia wartości źródła zastępczego $U_{AB}$ w schemacie zastępczym Thevenina. Obliczając kolejno prądy $I_1=\frac{E}{R_1+R_2}=1$ $I_2=\frac{E}{j{X}_L-j{X}_C}=2j$ $U_{AB}=R_1{I}_1-Z_C{I}_2=-15$ $I_2=\frac{E}{j{X}_L-j{X}_C}=2j$ napięcie $U_{AB}$ określa się ze wzoru $U_{AB}=R_1{I}_1-Z_C{I}_2=-15$

---

Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu $I$ określa się ze wzoru $I=\frac{U_{AB}}{Z_{AB}+R_0-j{X}_{C0}}=\frac{-15}{2,5+j10+7,5-j5}=\frac{-15}{11,18e^{j26^{\circ }}}=-1,34e^{-j26^{\circ }}$ Wartości chwilowe prądu $i(t)$ wyznaczane są z zależności $i(t)=-1,34\sqrt{2}sin(\omega t-26^{\circ })A$ Zauważmy, że zastosowanie twierdzenia Thevenina umożliwiło rozwiązanie obwodu względem jednego wybranego prądu bez konieczności rozwiązania układu równań algebraicznych. Metoda oparta na twierdzeniu Nortona Twierdzenie Nortona pozwala zastąpić złożony obwód elektryczny o dowolnej strukturze i wartościach elementów, przez obwód prosty będący połączeniem równoległym jednej impedancji zastępczej oraz idealnego źródła prądowego.

---

Twierdzenie [Twierdzenie Nortona] Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina. Rysunek na slajdzie 10 przedstawia schemat transformacji obwodu zgodnie z twierdzeniem Nortona.

---

Prąd $I$ oraz napięcie $U$ występujące w gałęzi AB obwodu oryginalnego są równe odpowiednio prądowi $I$ oraz napięciu $U$ w tej samej gałęzi obwodu uproszczonego. Źródło prądowe $I_Z$ występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja $Z_{AB}$ jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB reprezentowana jest przez impedancję $Z$, napięcie tej gałęzi oblicza się z prawa prądowego Kirchhoffa $I_Z-U(\frac{1}{Z}+\frac{1}{Z_{AB}})=0$, które pozwala wyrazić poszukiwane napięcie gałęzi w postaci $U=\frac{I_Z}{1/Z+1/Z_{AB}}$ Znajomość napięcia pozwala wyznaczyć na podstawie prawa Ohma prąd gałęzi korzystając z zależności $I=U/Z$ Podobnie jak metoda Thevenina, zastosowanie twierdzenia Nortona umożliwia obliczenie prądu i napięcia tylko jednej gałęzi obwodu. Zwykle z punktu widzenia obliczeniowego wygodniejsze jest użycie metody Thevenina.

---

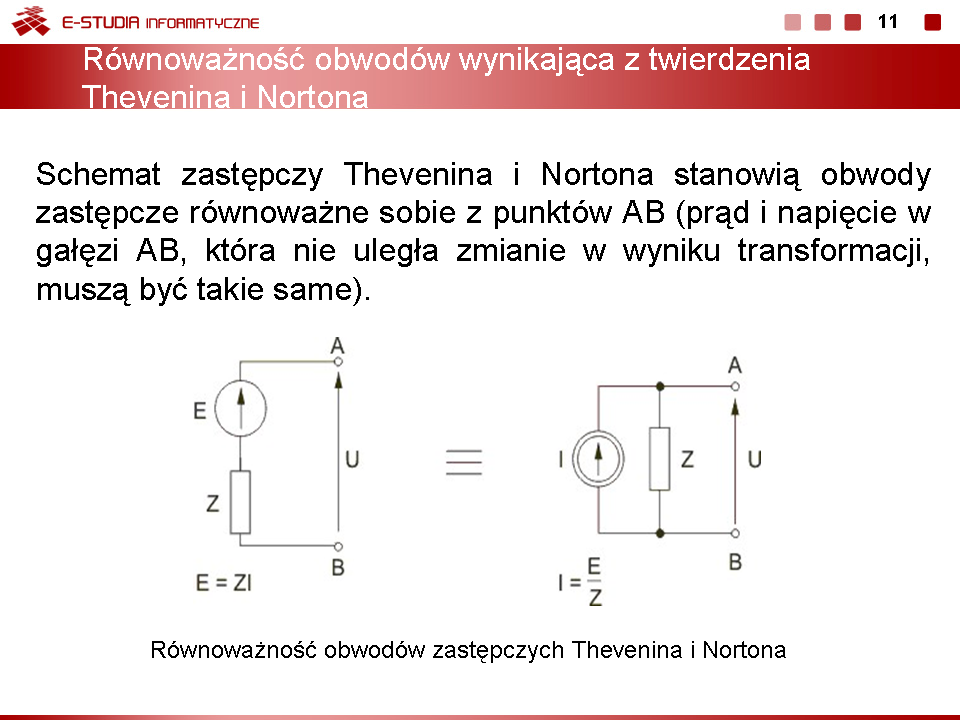
Równoważność twierdzenia Thevenina i Nortona Twierdzenia Thevenina i Nortona pozwalają wyznaczyć uproszczone schematy zastępcze tego samego układu elektrycznego z punktów AB obwodu wyjściowego. Oba schematy uproszczone stanowią więc obwody zastępcze równoważne sobie, co oznacza, że prąd i napięcie w gałęzi AB, która nie uległa zmianie w wyniku transformacji, są takie same. Oznacza to, że gałąź szeregowa zawierająca idealne źródło napięcia $E$ i impedancję $Z$ może być bez zmiany prądu w obwodzie zewnętrznym zastąpiona gałęzią równoległą zawierającą idealne źródło prądowe $I$ oraz impedancję $Z$, jak to zilustrowano na rysunku obok (slajd 11). Wzajemne relacje między wartościami źródła prądu i napięcia określa wzór $I=\frac{E}{Z}$ przy zamianie gałęzi szeregowej na równoległą oraz $E=ZI$ przy zamianie gałęzi równoległej na szeregową. Impedancja $Z$ w obu obwodach zastępczych pozostaje taka sama

---

Metoda potencjałów węzłowych Metoda potencjałów węzłowych, zwana również metodą węzłową, jest jedną z najogólniejszych i najczęściej stosowanych metod, pozwalających wyznaczyć prądy wszystkich gałęzi występujących w obwodzie. Jako zmienne przyjmuje się w niej potencjały poszczególnych węzłów obwodu określane względem jednego arbitralnie wybranego węzła uznanego za węzeł odniesienia („masy”), którego potencjał przyjmuje się za równy zeru. Liczba równań w tej metodzie jest równa liczbie węzłów niezależnych a więc znacznie mniejsza niż w metodzie wykorzystującej bezpośrednio układ równań otrzymanych w wyniku zastosowania praw Kirchhoffa. Metoda węzłowa wynika bezpośrednio z równań prądowych Kirchhoffa napisanych dla wszystkich węzłów niezależnych w obwodzie. Prąd każdej gałęzi obwodu jest wyrażany za pośrednictwem potencjałów węzłowych. Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci

---

---

---