Matematyka dyskretna 1/Ćwiczenia 5: Współczynniki dwumianowe: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu - "<div class="thumb t(.*)"><div style="width:(.*)px;"> <flash>file=(.*)\.swf\|width=(.*)\|height=(.*)<\/flash> <div\.thumbcaption>(.*)<\/div><\/div> <\/div>" na "$4x$5px|thumb|$1|$6" |
|||
| Linia 166: | Linia 166: | ||
</div></div> | </div></div> | ||
[[File:SW 8.CW1.svg|250x250px|thumb|right|SW 8.CW1.swf]] | |||
{{cwiczenie|6|cw 6| | {{cwiczenie|6|cw 6| | ||
| Linia 184: | Linia 181: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:SW 8.CW2.svg|250x250px|thumb|left|SW 8.CW2.swf]] | |||
[[File:SW 8.CW3.svg|250x250px|thumb|right|SW 8.CW3.swf]] | |||
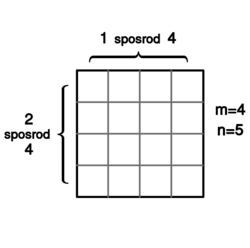
Policzmy ile prostokątów w kratce <math>\displaystyle n\times n</math> położonych jest w lewej górnej podkratce | Policzmy ile prostokątów w kratce <math>\displaystyle n\times n</math> położonych jest w lewej górnej podkratce | ||
| Linia 285: | Linia 276: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:SW 8.CW4.svg|250x250px|thumb|right|SW 8.CW4.swf]] | |||
Dowód indukcyjny względem <math>\displaystyle n</math>. Dla <math>\displaystyle n=0</math> i <math>\displaystyle n=1</math> mamy odpowiednio | Dowód indukcyjny względem <math>\displaystyle n</math>. Dla <math>\displaystyle n=0</math> i <math>\displaystyle n=1</math> mamy odpowiednio | ||
Wersja z 15:05, 3 paź 2021
Współczynniki dwumianowe
Ćwiczenie 1
Wskaż największy wyraz w -tym wierszu Trójkąta Pascala i odpowiedź uzasadnij.
Wskazówka
Rozwiązanie
Ćwiczenie 2
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 3
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 4
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
Ćwiczenie 5
Posługując się interpretacją kombinatoryczną pokaż, że
Wskazówka
Rozwiązanie
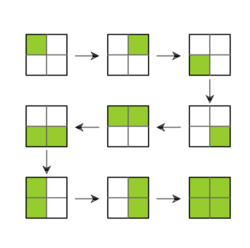
Ćwiczenie 6
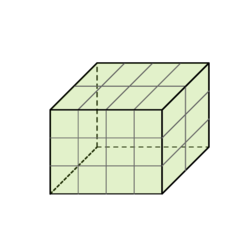
Ile prostokątów zawiera się w kratce ? Dla przykładu w kratce jest ich .
Wskazówka
Rozwiązanie
Ćwiczenie 7
Udowodnij, że:
Wskazówka
Rozwiązanie
Ćwiczenie 8
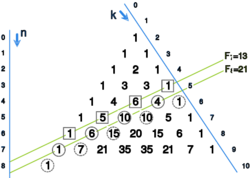
Udowodnij, że:
gdzie jest -tą liczbą Fibonacci'ego
Wskazówka
Rozwiązanie