PEE Moduł 1

---

Wykład 1 Podstawowe prawa obwodów elektrycznych

---

Podstawowe pojęcia obwodów Teoria obwodów stanowi jedną z dziedzin elektrotechniki zajmującą się stroną teoretyczną zjawisk występujących w obwodach elektrycznych, w tym metodami analizy rozpływu prądów i rozkładu napięć obwodu w stanie ustalonym i nieustalonym. Przyjmuje się, że nośnikami elektryczności są cząstki elementarne: elektrony i protony występujące w atomie. W przypadku przewodników elektrycznych najważniejszą rolę odgrywają elektrony swobodne, stanowiące trwałe nośniki ujemnego ładunku $q$, wyzwolone z przyciągania jądra atomu oraz jony, stanowiące cząsteczki naładowane dodatnio lub ujemnie. Ładunek elektryczny elektronu, oznaczany jest literą $e$ a jego wartość $e=1,602\cdot 10^{-19}C$. Prąd elektryczny powstaje jako uporządkowany ruch ładunków elektrycznych i jest utożsamiany w teorii obwodów z pojęciem natężenia prądu elektrycznego. W ogólności definiowany jest jako granica stosunku ładunku elektrycznego przepływającego przez przekrój poprzeczny elementu do rozpatrywanego czasu, gdy czas ten dąży do zera. Prąd elektryczny oznaczany będzie literą $i$ (dużą lub małą). Jest wielkością skalarną a jej jednostką w układzie SI jest amper ($A$). Prąd mierzymy przyrządem zwanym amperomierzem, włączanym szeregowo do gałęzi, której prąd chcemy zmierzyć. Przyjmuje się, że amperomierz ma impedancję wewnętrzną równą zeru, a więc nie wpływa na rozpływy prądów w obwodzie. Każdemu punktowi w środowisku przewodzącym prąd elektryczny można przyporządkować pewien potencjał mierzony względem punktu odniesienia. Różnica potencjałów między dwoma punktami tego środowiska nazywana jest napięciem elektrycznym. Jednostką napięcia elektrycznego jest volt ($V$). Napięcie pomiędzy dwoma punktami obwodu elektrycznego mierzymy zwykle przyrządem zwanym woltomierzem, włączanym równolegle między punkty, których różnicę potencjałów chcemy mierzyć. Przyjmuje się przy tym, że impedancja wewnętrzna woltomierza jest bliska nieskończoności, a więc woltomierz pomiarowy nie wpływa na rozkład napięć i rozpływ prądów w obwodzie. Elementy obwodu elektrycznego Za obwód elektryczny uważać będziemy takie połączenie elementów ze sobą, że istnieje możliwość przepływu prądu w tym połączeniu. Obwód jest odwzorowywany poprzez swój schemat, na którym zaznaczone są symbole graficzne elementów oraz sposób ich połączenia ze sobą, tworzący określoną strukturę.

---

Na strukturę obwodu elektrycznego poza elementami składają się również gałęzie, węzły i oczka. Gałąź obwodu jest tworzona przez jeden lub kilka elementów połączonych ze sobą w określony sposób. Węzłem obwodu jest zacisk będący końcówką gałęzi, do którego można dołączyć następną gałąź lub kilka gałęzi. Gałąź obwodu tworzą elementy ograniczone dwoma węzłami. Oczko obwodu to zbiór gałęzi połączonych ze sobą i tworzących drogę zamkniętą dla prądu elektrycznego. Oczko ma tę właściwość, że po usunięciu dowolnej gałęzi ze zbioru pozostałe gałęzie nie tworzą drogi zamkniętej. W obwodzie o zadanej strukturze istnieje ściśle określona liczba węzłów, natomiast liczba oczek jest wprawdzie skończona ale bliżej nieokreślona.

---

Element jest częścią składową obwodu niepodzielną pod względem funkcjonalnym bez utraty swych cech charakterystycznych. Na elementy obwodu składają się źródła energii elektrycznej oraz elementy akumulujące energię lub rozpraszające ją. W każdym elemencie mogą zachodzić dwa lub nawet wszystkie trzy wymienione tu procesy, choć jeden z nich jest zwykle dominujący. Element jest idealny jeśli charakteryzuje go tylko jeden rodzaj procesu energetycznego. Elementy posiadające zdolność akumulacji oraz rozpraszania energii tworzą klasę elementów pasywnych. Nie wytwarzają one energii a jedynie ją przetwarzają. Najważniejsze z nich to rezystor, kondensator oraz cewka. Elementy mające zdolność generacji energii nazywane są źródłami. Zaliczamy do nich niezależne źródło napięcia i prądu oraz źródła sterowane. Każdy element obwodu może być opisany równaniami algebraicznymi lub różniczkowymi, wiążącymi prąd i napięcie na jego zaciskach. Element jest liniowy, jeśli równanie opisujące go jest liniowe. W przeciwnym wypadku element jest nieliniowy.

---

Rezystor Rezystor, zwany również opornikiem należy do klasy elementów pasywnych rozpraszających energię. W teorii obwodów rezystor uważa się za element idealny i przypisuje mu tylko jedną cechę (parametr), zwaną rezystancją lub oporem. W dalszej części rozważać będziemy wyłącznie rezystor liniowy. Rezystancję (oporność) oznaczać będziemy literą $R$ a jej odwrotność jest nazywana konduktancją i oznaczana literą $G$, przy czym $R=1/G$. Symbol graficzny rezystora liniowego przedstawiony jest na rysunku obok. Opis matematyczny rezystora wynika z prawa Ohma, zgodnie z którym $u_R=R_{i_R}$ Wartość rezystancji rezystora liniowego przyjmuje określoną wartość (często stałą). Jednostką rezystancji jest om ($\mathrm{\Omega }$) a konduktancji siemens ($S$). W realizacji praktycznej opornik jest wykonywany często z drutu metalowego o długości $l$, polu przekroju poprzecznego $S$ i rezystancji właściwej $\rho$. Rezystancja takiego opornika jest wprost proporcjonalna do $l$ i $\rho$ a odwrotnie proporcjonalna do $S$, stąd $R=\rho l/S$.

---

Cewka Cewka zwana również induktorem należy również do klasy elementów pasywnych. Ma zdolność gromadzenia energii w polu magnetycznym. Cewce idealnej przypisuje się tylko jedną właściwość, zwaną indukcyjnością własną (w skrócie indukcyjnością) $L$. W przypadku cewki liniowej indukcyjność definiuje się jako stosunek strumienia $\mathrm{\Psi }$ skojarzonego z cewką do prądu płynącego przez nią, to znaczy $L=\frac{\mathrm{\Psi }}{i_L}$ Strumień skojarzony $\mathrm{\Psi }$ cewki o z zwojach jest równy sumie strumieni wszystkich zwojów cewki, to jest $\mathrm{\Psi }=z\varphi$ ($\varphi$ - strumień skojarzony z jednym zwojem cewki, $z$ – liczba zwojów). Jednostką indukcyjności jest henr ($H$), przy czym $1H=1\mathrm{\Omega }s$. Napięcie cewki wyrażone jest jako pochodna strumienia względem czasu $u_L=\frac{d\mathrm{\Psi }}{dt}$ W przypadku cewki liniowej o indukcyjności $L$ niezależnej od czasu, dla której strumień jest iloczynem prądu $i$ indukcyjności $L$, $\mathrm{\Psi }=L{i}_L$, relacja napięciowo-prądowa upraszcza się do postaci $u_L=L\frac{d{i}_L}{dt}$ Zauważmy, że przy stałej wartości prądu cewki i stałej wartości indukcyjności $L$ napięcie na niej jest równe zeru, gdyż pochodna wartości stałej względem czasu jest równa zeru. Stąd cewka w stanie ustalonym obwodu przy prądzie stałym zachowuje się jak zwarcie (napięcie między końcówkami elementu równe zeru).

---

Kondensator Kondensator jest elementem pasywnym, w którym istnieje możliwość gromadzenia energii w polu elektrycznym. Kondensatorowi idealnemu przypisuje się tylko jedną właściwość zwaną pojemnością $C$. W przypadku kondensatora liniowego pojemność $C$ jest definiowana jako stosunek ładunku $q$ zgromadzonego w kondensatorze do napięcia między okładzinami tego kondensatora $C=\frac{q}{u_C}$ W układzie SI jednostką ładunku jest kulomb ($C$), a pojemności farad ($F$), przy czym $1F=1C/V$. Zależność wiążąca napięcie i prąd kondensatora dana jest w postaci równania różniczkowego Podobnie jak w przypadku cewki, jeśli napięcie na zaciskach kondensatora jest stałe, jego prąd jest równy zeru (pochodna wartości stałej względem czasu jest zerem). Kondensator zachowuje się wtedy jak przerwa (pomimo istnienia napięcia prąd nie płynie).

---

Niezależne źródło napięcia i prądu Źródło niezależne prądu bądź napięcia, zwane w skrócie źródłem prądu i źródłem napięcia, jest elementem aktywnym, generującym energię elektryczną, powstającą zwykle z zamiany innego rodzaju energii, na przykład z energii mechanicznej, słonecznej, jądrowej itp. W teorii obwodów rozważać będziemy źródła idealne należące do klasy źródeł napięciowych bądź prądowych. Symbol idealnego niezależnego źródła napięcia przedstawiony jest obok na rys. a, natomiast źródła prądu na rys. b.

---

Niezależne źródła prądu i napięcia mają następujące właściwości: Napięcie na zaciskach idealnego źródła napięcia nie zależy od prądu przepływającego przez to źródło, a zatem nie zależy od jego obciążenia. Przy stałym napięciu $u$ panującym na zaciskach oraz prądzie $i$ wynikającym z obciążenia, rezystancja wewnętrzna idealnego źródła napięciowego, definiowana jest w postaci zależności różniczkowej $R_W=\frac{du}{di}=0$. Stąd idealne źródło napięcia charakteryzuje się rezystancją wewnętrzna równą zeru (zwarcie z punktu widzenia rezystancyjnego). Prąd idealnego źródła prądu nie zależy od obciążenia tego źródła, a więc od napięcia panującego na jego zaciskach. Przy stałym prądzie płynącym przez idealne źródło prądowe i dowolnym (bliżej nieokreślonym) napięciu panującym na jego zaciskach rezystancja wewnętrzna idealnego źródła prądowego jest równa nieskończoności. Stąd idealne źródło prądowe z punktu widzenia rezystancyjnego reprezentuje sobą przerwę. Rysunek na poprzednim slajdzie przedstawia charakterystyki prądowo-napięciowe obu rodzajów idealnych źródeł niezależnych: napięcia (a) i prądu (b). Dla źródła napięciowego charakterystyka jest równoległa do osi prądowej (wartość napięcia $u$ stała), a dla źródła prądowego równoległa do osi napięciowej (wartość prądu $i$ stała). Tak podane charakterystyki odnoszą się do źródeł stałych. W przypadku źródeł sinusoidalnych idealność jest rozumiana jako stałość parametrów źródła (amplituda, faza początkowa oraz częstotliwość niezależne od obciążenia). Przykładami źródła napięcia stałego jest akumulator, źródła napięcia zmiennego - generator synchroniczny, źródła prądowego - elektroniczny zasilacz prądowy o stabilizowanym, niezależnym od obciążenia prądzie, itp.

---

Źródła sterowane prądu i napięcia W odróżnieniu od źródeł niezależnych, których prąd lub napięcie (bądź parametry charakteryzujące je, np. amplituda i częstotliwość) były stałe, ustalone na etapie wytworzenia, źródła sterowane z definicji zależą od wielkości sterujących, którymi mogą być prąd lub napięcie dowolnego innego elementu w obwodzie. Źródło sterowane jest więc elementem czterozaciskowym i charakteryzuje się tym, że napięcie lub prąd na jego zaciskach wyjściowych są proporcjonalne do napięcia lub prądu związanego z druga parą zacisków sterujących. Wyróżnić można cztery rodzaje źródeł sterowanych: źródło napięcia sterowane napięciem, źródło napięcia sterowane prądem, źródło prądu sterowane napięciem i źródło prądu sterowane prądem. Równania źródeł starowanych źródło napięcia sterowane napięciem, opisane równaniem $u_2=a{u}_1$ źródło napięcia sterowane prądem, opisane równaniem $u_2=r{i}_1$ źródło prądu sterowane napięciem, opisane równaniem $i_2=g{u}_1$ źródło prądu sterowane prądem, opisane równaniem $i_2=b{i}_1$

---

Schematy graficzne wszystkich wymienionych tu rodzajów źródeł sterowanych prądu i napięcia przedstawione są na rysunku na poprzednim slajdzie. Wielkości $r$, $g$ oraz $a$ i $b$ stanowią współczynniki proporcjonalności między wielkością sterująca i sterowaną tych źródeł. Przyjmują one najczęściej wartości rzeczywiste, choć w różnego rodzaju modelach mogą być również opisane funkcją zespoloną. Należy nadmienić, że źródła sterowane stanowią bardzo popularne modele wielu elementów elektrycznych i elektronicznych, takich jak transformatory idealne, maszyny elektryczne, tranzystory bipolarne i polowe, wzmacniacze operacyjne napięciowe i prądowe, itp.

---

Prawa Kirchhoffa Pod pojęciem analizy obwodu elektrycznego rozumie się proces określania rozpływu prądów i rozkładu napięć w obwodzie przy założeniu, że znana jest struktura obwodu oraz wartości wszystkich jego elementów. Podstawę analizy obwodów elektrycznych stanowią prawa Kirchhoffa, podane przez niemieckiego fizyka Gustawa Kirchhoffa w dziewiętnastym wieku. Wyróżnia się dwa prawa określające rozpływ prądów i rozkład napięć w obwodzie. Pierwsze prawo Kirchhoffa kojarzy się zwykle z bilansem prądów w węźle obwodu elektrycznego a drugie z bilansem napięć w oczku. Prawo prądowe Suma prądów w każdym węźle obwodu elektrycznego jest równa zeru $\sum _k=i_k=0$ Sumowanie dotyczy wszystkich prądów, które dopływają lub odpływają z danego oczka, przy czym wszystkie prądy wpływające do węzła brane są z jednakowym znakiem a wszystkie prądy wypływające z węzła ze znakiem przeciwnym (nie jest istotne czy znak plus dotyczy prądów wpływających czy wypływających). Sposób tworzenia równania prądowego Kirchhoffa zilustrujemy dla jednego węzła obwodu przedstawionego na rysunku obok. Prawo Kirchhoffa dla tego węzła z uwzględnieniem kierunków prądów w węźle zapiszemy w postaci: $i_1+i_2+i_3-i_4-i_5=0$ Można je również zapisać jako bilans prądów dopływających i odpływających od węzła w postaci: $i_1+i_2+i_3=i_4+i_5$ Dla każdego obwodu można napisać dokładnie $n-1$ niezależnych równań prądowych, gdzie $n$ oznacza całkowitą liczbę węzłów a $(n-1)$ liczbę węzłów niezależnych. Bilans prądów w pozostałym $n$-tym węźle obwodu wynika z równań prądowych napisanych dla $n-1$ węzłów (jest to węzeł zależny zwany węzłem odniesienia). Wybór węzła odniesienia jest całkowicie dowolny. Prawo napięciowe Suma napięć w każdym oczku obwodu elektrycznego jest równa zeru $\sum _k=u_k=0$ Sumowanie dotyczy napięć gałęziowych występujących w danym oczku zorientowanych względem dowolnie przyjętego kierunku odniesienia. Napięcie gałęziowe zgodne z tym kierunkiem jest brane z plusem a przeciwne z minusem. Sposób pisania równań wynikających z prawa napięciowego Kirchhoffa pokażemy na przykładzie oczka obwodu przedstawionego na rysunku obok. Uwzględniając kierunki napięć gałęziowych równanie napięciowe Kirchhoffa dla tego oczka przyjmie postać: $u_1+u_2+u_3-u_4-e=0$ Można je również zapisać jako bilans napięć źródłowych i odbiornikowych w postaci: $e=u_1+u_2+u_3-u_4$ Dla każdego obwodu można napisać tyle równań oczkowych ile oczek wyodrębnimy w tym obwodzie, przy czym część równań oczkowych będzie równaniami zależnymi (wynikającymi z liniowej kombinacji innych równań). Liczba równań oczkowych branych pod uwagę w analizie jest więc równa liczbie oczek niezależnych.

---

Przykład Napiszmy równania Kirchhoffa dla obwodu z rysunku na slajdzie 14. Zgodnie z prawami Kirchhoffa równania obwodu przyjmą następującą postać: Równania prądowe: $i_{L1}-i_{L2}-i_C=0$ $i_{L2}-i_{R1}-i_{R2}=0$ $i_{L1}=i$ Równania napięciowe: $u_C-u_{L2}-u_{R1}=0$ $u_{R1}-u_{R2}-e=0$ Przedstawiony tu układ równań jest wystarczający do uzyskania wszystkich innych wielkości prądowych bądź napięciowych w obwodzie. Należy go jedynie uzupełnić o równania definicyjne wiążące prąd i napięcie każdego elementu. Po takim uzupełnieniu uzyskuje się pełny opis obwodu a jego rozwiązanie pozwala wyznaczyć rozpływ prądów i rozkład napięć w obwodzie. Szczególnie proste zależności otrzymuje się dla obwodu rezystancyjnego, zawierającego oprócz źródeł wymuszających jedynie rezystory oraz (ewentualnie) źródła sterowane o rzeczywistych współczynnikach sterowania. Dla takich obwodów równania elementów rezystancyjnych są dane w postaci zależności algebraicznych, które wstawione do równań Kirchhoffa pozwalają utworzyć układ równań algebraicznych o liczbie zmiennych równych liczbie równań. Sposób tworzenia takiego układu równań pokażemy na przykładzie obwodu z rys. na slajdzie 15.

---

---

Z równań Kirchhoffa otrzymuje się: $i_{Z1}-i_1-i_2-i_4=0$ $i_2+i_4+i_{Z2}-i_3=0$ $u_{R1}-u_{R2}+e-u_{R3}=0$ $u_{R2}-e-u_{R4}=0$ Równania elementów rezystancyjnych: $u_{R1}=R_1{i}_1$, $u_{R2}=R_2{i}_2$, $u_{R3}=R_3{i}_3$, $u_{R4}=R_4{i}_4$ tworzą wspólnie z równaniami Kirchhoffa następujący układ równań algebraicznych: $i_1+i_2+i_4=i_{Z1}$ $i_2-i_3+i_4=-i_{Z2}$ $R_1{i}_1-R_2{i}_2-R_3{i}_3=-e$ $R_2{i}_2-R_4{i}_4=e$ Po wstawieniu danych liczbowych do powyższych równań otrzymuje się: $i_1+i_2+i_4=2$ $i_2-i_3+i_4=-5$ $i_1-2i_2-3i_3=-10$ $2i_2-4i_4=10$ W wyniku rozwiązania tego układu równań otrzymuje się: $i_1=3,187A$, $i_2=0,875A$, $i_3=3,812A$ oraz $i_4=-2,062A$. Łatwo sprawdzić przez podstawienie obliczonych wartości do układu równań, że bilans prądów w każdym węźle oraz bilans napięć w każdym oczku obwodu jest zerowy.

---

Przekształcenia obwodów W analizie obwodów elektrycznych ważną rolę odgrywa upraszczanie struktury obwodu, polegające na zastępowaniu wielu elementów połączonych szeregowo lub równolegle poprzez jeden element zastępczy. Umożliwia to zmniejszenie liczby równań w opisie obwodu i uproszczenie etapu rozwiązania tych równań. Wyróżnić można cztery podstawowe rodzaje połączeń elementów, do których stosuje się przekształcenie. Są to: połączenie szeregowe połączenie równoległe połączenie gwiazdowe połączenie trójkątne. Układ połączenia szeregowego elementów W połączeniu szeregowym elementów koniec jednego elementu jest bezpośrednio połączony z początkiem następnego. Rys. na slajdzie 17 przedstawia schemat ogólny połączenia szeregowego rezystorów. Prąd każdego elementu obwodu jest jednakowy i równy $i$, natomiast napięcie na zaciskach zewnętrznych obwodu jest równe sumie napięć poszczególnych elementów tworzących połączenie. Napięciowe równanie Kirchhoffa dla obwodu (z rysunku na slajdzie 17) przyjmuje więc postać: $u=(R_1+R_2+...+R_N)i$ Przy oznaczeniu sumy rezystancji przez $R$ $R=R_1+R_2+...+R_N$ otrzymuje się uproszczenie $N$ rezystorów połączonych szeregowo do jednego rezystora zastępczego o rezystancji $R$ opisanej wzorem na slajdzie 20 ($R_{12}$). Rezystancja wypadkowa połączenia szeregowego rezystorów jest równa sumie rezystancji poszczególnych elementów tworzących to połączenie.

---

W połączeniu równoległym początki i końce wszystkich elementów są ze sobą bezpośrednio połączone, jak to pokazano dla elementów rezystancyjnych na rysunku obok (slajd 18). Z połączenia tego wynika, że napięcie na wszystkich elementach jest jednakowe a prąd wypadkowy jest równy sumie prądów wszystkich elementów obwodu. Prądowe prawo Kirchhoffa dla obwodu z rysunku można więc zapisać w postaci: $i=(G_1+G_2+...+G_N)u$ przy czym $G_i(i=1,2,...,N)$ stanowią konduktancje rezystorów, $G_i=1/R_i$. Przy oznaczeniu sumy konduktancji przez $G$, gdzie $G=G_1+G_2+...+G_N$ otrzymuje się uproszczenie $N$ rezystorów połączonych równolegle do jednego rezystora zastępczego o konduktancji $G$ opisanej wzorem na slajdzie 20 ($R_{31}$). Jak widać w połączeniu równoległym rezystorów konduktancja wypadkowa jest równa sumie konduktancji poszczególnych rezystorów. Szczególnie prosty jest wzór na rezystancję zastępczą dla 2 rezystorów połączonych równolegle. W tym przypadku $G=G_1+G_2$. Uwzględniając, że $G=1/R$ po prostych przekształceniach otrzymuje się $R=\frac{R_1{R}_2}{R_1+R_2}$ Należy jednak podkreślić, że przy trzech (i więcej) elementach połączonych równoległe wygodniejsze jest operowanie na konduktancjach a przejście na rezystancję zastępczą wykonuje się w ostatnim kroku po ustaleniu wartości sumy konduktancji.

---

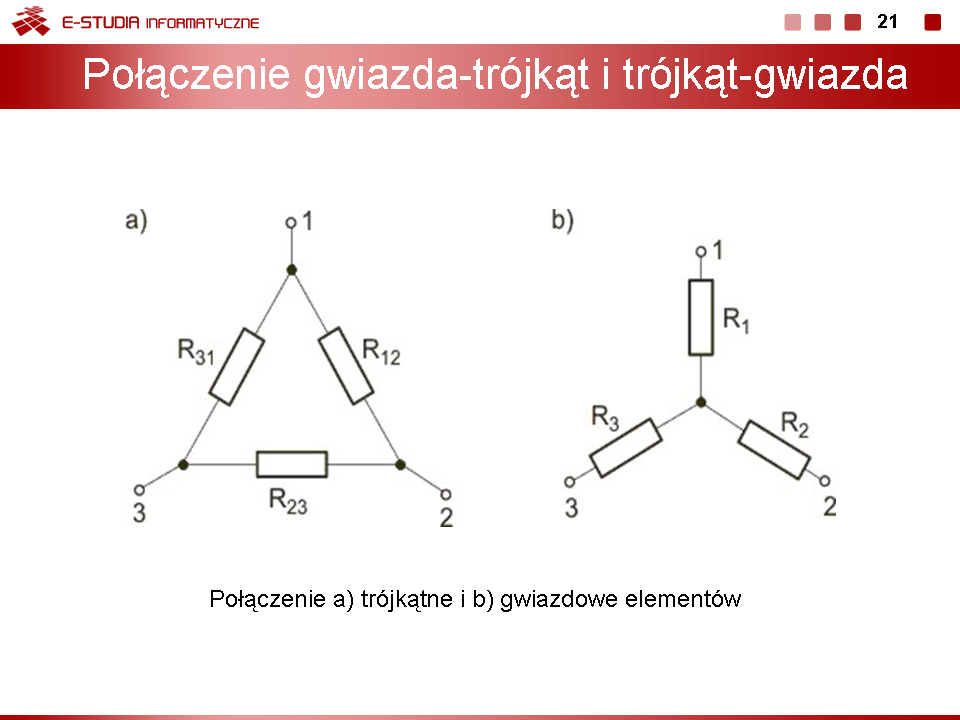
Transfiguracja gwiazda-trójkąt i trójkąt-gwiazda Operowanie uproszczonym schematem wynikającym z połączenia szeregowego i równoległego elementów jest najwygodniejszym sposobem redukcji obwodu. W przypadku gdy nie ma elementów połączonych szeregowo czy równolegle możliwe jest dalsze uproszczenie przez zastosowanie przekształcenia gwiazda-trójką lub trójkąt-gwiazda. Oznaczenia elementów obwodu trójkąta i gwiazdy są przedstawione na rysunku obok (slajd 19).

---

Transfiguracja trójkąta na gwiazdę lub gwiazdy na trójkąt polega na przyporządkowaniu danej konfiguracji elementów konfiguracji zastępczej, równoważnej jej z punktu widzenia zacisków zewnętrznych (te same prądy przy tych samych napięciach międzyzaciskowych). Dla uzyskania niezmienionych prądów zewnętrznych obwodu gwiazdy i trójkąta rezystancje między parami tych samych zacisków gwiazdy i trójkąta powinny być takie same. Zostało udowodnione, że warunki powyższe są automatycznie spełnione, jeśli przy zamianie gwiazdy na trójkąt spełnione są następujące warunki na rezystancje $R_{12}=R_1+R_2+\frac{R_1{R}_2}{R_3}$ $R_{23}=R_2+R_3+\frac{R_2{R}_3}{R_1}$ $R_{31}=R_3+R_1+\frac{R_3{R}_1}{R_2}$

---

Podobnie przy zamianie trójkąta na gwiazdę rezystancje gwiazdy muszą spełniać warunki $R_1=\frac{R_{12}{R}_{31}}{R_{12}{R}_{23}{R}_{31}}$ $R_2=\frac{R_{23}{R}_{12}}{R_{12}{R}_{23}{R}_{31}}$ $R_3=\frac{R_{31}{R}_{23}}{R_{12}{R}_{23}{R}_{31}}$ Przekształcenia równoważne obwodu wykorzystujące reguły połączenia szeregowego, równoległego oraz przekształcenia gwiazda-trójkąt i trójkąt-gwiazda umożliwiają dalszą redukcję tego obwodu i po wykonaniu odpowiedniej liczby przekształceń sprowadzenie go do pojedynczego elementu zastępczego.

---

---