PEE Moduł 2

Wykład 2 Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym

---

Parametry sygnału sinusoidalnego Sygnały sinusoidalne zwane również harmonicznymi są opisane w dziedzinie czasu następującym wzorem (w opisie przyjęto oznaczenie sygnału napięciowego) $u(t)=U_{m}sin(\omega t+\psi )$ Wielkości występujące w opisie mają następujące nazwy i oznaczenia: $u(t)$- wartość chwilowa napięcia $U_m$- wartość maksymalna (szczytowa) napięcia zwana również amplitudą $\psi$- faza początkowa napięcia odpowiadająca chwili t=0 Parser nie mógł rozpoznać (nieznana funkcja „\omegat”): {\displaystyle \omegat+\psi} - kąt fazowy napięcia w chwili t $f=1/T$- częstotliwość mierzona w hercach (Hz) $T$- okres przebiegu sinusoidalnego $\omega =2\pi f$- pulsacja mierzona w radianach na sekundę. Wartości chwilowe sygnałów oznaczać będziemy małą literą a wartości maksymalne, skuteczne i wielkości operatorowe dużą. Rys. 2.1 przedstawia przebieg sygnału sinusoidalnego napięcia z oznaczeniami poszczególnych jego parametrów. Oś odciętych ma podwójne oznaczenie: czasu oraz fazy (aktualny kąt fazowy).

---

Przebiegi zmienne w czasie dobrze charakteryzuje wartość skuteczna. Dla przebiegu okresowego $f(t)$ o okresie $T$ jest ona definiowana w postaci Parser nie mógł rozpoznać (błąd składni): {\displaystyle F=\sqrt\left \frac{1}{T} \right \int_{t_0}^{t_o+T}f^2(t)dt } Łatwo udowodnić, że wartość skuteczna przebiegu okresowego nie zależy od wybory fazy początkowej. W przypadku przebiegu sinusoidalnego napięcia $u(t)=U_{m}sin(\omega t+\psi )$ jest równa Parser nie mógł rozpoznać (błąd składni): {\displaystyle U=\left \frac{U_m}{\sqrt 2} \right} a w przypadku prądu sinusoidalnego $i(t)=U_{m}sin(\omega t+\psi )$ Parser nie mógł rozpoznać (błąd składni): {\displaystyle I=\left \frac{I_m}{\sqrt 2} \right} Dla sygnału sinusoidalnego wartość skuteczna jest więc $\sqrt{2}$ razy mniejsza niż jego wartość maksymalna. Należy zauważyć, że napięcie stałe $u(t)=U$ jest szczególnym przypadkiem sygnału sinusoidalnego, dla którego częstotliwość jest równa zeru $(f=0)$ a wartość chwilowa jest stała i równa $u(t)=U_{m}sin()=U$. Jest to ważna właściwość, gdyż dzięki temu metody analizy obwodów o wymuszeniu sinusoidalnym mogą mieć zastosowanie również do wymuszeń stałych przy założeniu $f=0$. Dla sygnału stałego wartość maksymalna i skuteczna są sobie równe i równają się danej wartości stałej.

---

Metoda symboliczna liczb zespolonych analizy obwodów RLC Analiza obwodów zawierających elementy RLC przy wymuszeniu sinusoidalnym napotyka na pewne trudności związane z wystąpieniem w opisie cewki i kondensatora równań różniczkowych. Trudności te łatwo jest pokonać w stanie ustalonym. Stanem ustalonym obwodu nazywać będziemy taki stan, w którym charakter odpowiedzi jest identyczny jak charakter wymuszenia, to znaczy odpowiedzią na wymuszenie sinusoidalne jest odpowiedź również sinusoidalna o tej samej częstotliwości choć o różnej amplitudzie i fazie początkowej. Dla stanu ustalonego obwodu wprowadzona zostanie metoda liczb zespolonych, zwana również metodą symboliczną, sprowadzająca wszystkie operacje różniczkowe i całkowe do działań algebraicznych na liczbach zespolonych.

---

WDla wprowadzenia tej metody przyjmijmy, że rozważany jest obwód szeregowy RLC zasilany ze źródła napięcia sinusoidalnego $u(t)=U_{m}sin(\omega t+\psi )$ Z prawa napięciowego Kirchhoffa wynika następujący związek między napięciami elementów tego obwodu $u(t)=u_R+u_L+u_C$ Biorąc pod uwagę podstawowe zależności definicyjne dla rezystora, cewki i kondensatora $u_R=Ri$ $u_c=1/C\int idt$ Parser nie mógł rozpoznać (błąd składni): {\displaystyle u_L=L \left \frac{di}{dt} \right} otrzymuje się Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_m sin(\omega t+\psi)=R_i+ \left \frac{1}{C} \right \int idt+L \left \frac{di}{dt} \right}

---

Jest to równanie różniczkowo-całkowe opisujące zależności między wartościami chwilowymi prądu i napięcia wymuszającego w obwodzie. Pełne rozwiązanie tego równania sprowadza się do wyznaczenia dwu składowych prądu, stanowiących odpowiedź obwodu w stanie ustalonym i stanie przejściowym: składowej ustalonej, której charakter zmian w czasie jest taki sam jak sygnału wymuszającego (przy sinusoidalnym wymuszeniu odpowiedź również sinusoidalna o tej samej częstotliwości); jest to stan który zostanie osiągnięty przez obwód po czasie teoretycznie dążącym do nieskończoności. składowej przejściowej odpowiadającej różnicy między rozwiązaniem rzeczywistym równania różniczkowego a składową ustaloną. Składowa przejściowa zanika zwykle szybko w czasie i pozostaje jedynie składowa ustalona. Stan po zaniknięciu składowej przejściowej nazywamy stanem ustalonym obwodu.

---

Składową ustaloną prądu w obwodzie można otrzymać nie rozwiązując równania różniczkowego opisującego ten obwód a korzystając jedynie z metody liczb zespolonych (metody symbolicznej). Istotnym elementem tej metody jest zastąpienie przebiegów czasowych ich reprezentacją zespoloną. Przyjmijmy, że prąd $i(t)=I_{m}sin(\omega t+\psi )$ oraz napięcie $u(t)=U_{m}sin(\omega t+\psi )$ zastąpione zostały przez wektory wirujące w czasie, odpowiednio $I(t)$ oraz $U(t)$ określone w postaci $U(t)=U_m{e}^j{}^{\psi }{e}^j{}^{\omega }{}^t$ $I(t)=I_m{e}^j{}^{{\psi }_i}{e}^j{}^{\omega }{}^t$ Po zastąpieniu wartości czasowych prądu i napięcia w równaniu (2.12) poprzez ich reprezentację w postaci wektorów wirujących otrzymuje się Parser nie mógł rozpoznać (błąd składni): {\displaystyle U(t)=RI(t)+L \left \frac{dI(t)}{dt} \right+\frac{1}{C} \int I(t)dt}

---

Po wykonaniu operacji różniczkowania i całkowania równanie powyższe przyjmuje postać $\frac{U_m}{\sqrt{2}}{e}^j{}^{\psi }=R\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}+j\omega L\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}+\frac{1}{j\omega C}\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}$ Oznaczmy przez $u=\frac{U_m}{\sqrt{2}}{e}^j{}^w$ wartość skuteczną zespoloną napięcia, a przez $I=\frac{I_m}{\sqrt{2}}{e}^j{}^w$ wartość skuteczną zespoloną prądu. Wtedy równanie (2.10) można zapisać w następującej postaci obowiązującej dla wartości skutecznych zespolonych $U=RI+j\omega LI+\frac{1}{j\omega C}I$

---

Składnik $U_r=RI$ odpowiada napięciu skutecznemu zespolonemu na rezystorze. Wielkość $U_L=j\omega LI$ reprezentuje wartość skuteczną zespoloną napięcia na cewce, a składnik $U_c=\frac{1}{j\omega C}I$ odpowiada wartości skutecznej zespolonej napięcia na kondensatorze. Wszystkie napięcia i prąd w obwodzie są wartościami zespolonymi.

---

Analizując postać równania (2.11) można zauważyć prostą analogię do równania opisującego obwód rezystancyjny. W tym celu wprowadzimy uogólnienie rezystancji w postaci pojęcia impedancji zespolonej wiążącej wartości skuteczne prądu i napięcia na elementach R, L, C w stanie ustalonym przy wymuszeniu sinusoidalnym. Z ostatnich równań na podstawie prawa Ohma można napisać następujące przyporządkowania: Dla rezystora $Z_R=R$ impedancja $Z_R$ jest równa rezystancji tego rezystora. Dla cewki $Z_L=j\omega L$ impedancja $Z_L$ jest liczbą zespoloną (urojoną) zależną liniowo od częstotliwości. Dla kondensatora $Z_C=\frac{1}{j\omega C}=-j\frac{1}{\omega C}$ impedancja$Z_C$ jest także zespolona i odwrotnie proporcjonalna do częstotliwości. Wartość $X_L=\omega L$ nosi nazwę reaktancji indukcyjnej a wartość $X_C=\frac{1}{\omega C}$ reaktancji pojemnościowej. W związku z powyższym można napisać $Z_L=j{X}_L,Z_C=-j{X}_C$

---

Wprowadzając oznaczenie wypadkowej impedancji obwodu przez $Z$, gdzie $Z=Z_R+Z_L+Z_C$ zależność prądowo-napięciową w obwodzie szeregowym RLC można zapisać w postaci, znanej jako prawo Ohma dla wartości symbolicznych $U=ZL$ lub $I=\frac{U}{Z}=|I|e^j{}^w$ gdzie moduł prądu $|I|=\frac{|U|}{|Z|}=\frac{|U|}{{\sqrt{R}}^2+(\omega L-1/(\omega C){)}^2}$ natomiast kąt fazowy prądu ${\psi }_i=\psi -arctg\frac{\omega L-1/(\omega C)}{R}$ Faza początkowa wektora napięcia wymuszającego jest tu oznaczona przez $\psi$ , a faza początkowa wektora prądu – przez ${\psi }_i$ Różnica faz nazywana jest przesunięciem fazowym prądu względem napięcia i oznaczana literą $\phi$ , przy czym $\phi =\psi -{\psi }_i=arctg\frac{\omega L-1/(\omega C)}{R}$ Kąt przesunięcia fazowego $\phi$ odgrywa ogromną rolę w elektrotechnice, zwłaszcza w zagadnieniach mocy. Kąt ten jest uważany za dodatni dla obwodów o charakterze indukcyjnym a za ujemny dla obwodów o charakterze pojemnościowym. Zauważmy, że wartościom skutecznym zespolonym prądu oraz napięcia można przyporządkować funkcję czasu. Biorąc pod uwagę, że przejście z przebiegu czasowego na opis zespolony (symboliczny) odbywa się według schematu $u(t)=U_{m}sin(\omega t+\psi )\to \frac{U_m}{\sqrt{2}}{e}^j{}^{\psi }$ powrót z wartości zespolonej do postaci czasowej polega na pomnożeniu modułu wartości skutecznej przez $\sqrt{2}$ i uzupełnieniu wyniku przez dopisanie funkcji$sin(\omega t+\psi )$ Stąd przykładowo, jeśli wynik zespolony prądu dany jest w postaci $I=10e^{50^o}$ , to odpowiadający mu przebieg czasowy ma postać $i(t)=10\sqrt{2}sin(\omega t+50^o)$ Istnieje również ścisła analogia między konduktancją (odwrotność rezystancji) a odwrotnością impedancji. Analogicznie do pojęcia konduktancji w obwodzie rezystancyjnym wprowadza się pojęcie admitancji zespolonej dla obwodu RLC. Admitancja jest definiowana jako odwrotność impedancji. Oznaczana jest najczęściej literą $Y$, przy czym $Y=1/Z$ Admitancja kondensatora jest równa $Y_C=j\omega C$ , cewki $Y_L=\frac{1}{j\omega L}=-\frac{1}{\omega L}$ natomiast admitancja rezystora jest równa jego konduktancji $Y_R=G=1/R.$ Podobnie odwrotność reaktancji X nosi specjalną nazwę susceptancji. Wartość susceptancji dla kondensatora jest równa $B_C=\omega C$ natomiast dla cewki $B_L=1/\omega L$

---

Prawa Kirchhoffa dla wartości symbolicznych Przy zastąpieniu wartości rzeczywistych przez wartości zespolone równania różniczkowe zostały zastąpione przez równania algebraiczne. Nastąpiła zatem algebraizacja równań opisujących obwód. Wszystkie elementy RLC traktowane są w podobny sposób i reprezentowane przez swoje impedancje symboliczne w postaci zespolonej. Impedancje zespolone mogą być interpretowane jako uogólnienie rezystancji. Dla obwodu reprezentowanego w postaci symbolicznej obowiązują prawa Kirchhoffa, które mają identyczną postać jak dla obwodu rzeczywistego, z tą różnicą, że zamiast wielkości chwilowych używa się wielkości zespolonych. Prawo prądowe Kirchhoffa Suma algebraiczna prądów zespolonych w dowolnym węźle obwodu elektrycznego jest równa zeru, co zapiszemy w postaci $\sum _k{l}_k=0$ W równaniu tym wszystkie prądy dane są w postaci zespolonej. Prawo napięciowe Kirchhoffa Suma algebraiczna napięć zespolonych w każdym oczku obwodu elektrycznego jest równa zeru, co zapiszemy w postaci $\sum _k{U}_k=0$ W równaniu tym symbolem $U$ oznaczono wszystkie napięcia w postaci zespolonej, zarówno na gałęziach pasywnych jak i źródłowych obwodu. Sposób sumowania (znak plus lub minus) zarówno prądów jak i napięć jest taki sam jak w przypadku operowania wartościami rzeczywistymi.

---

Podsumowując, na metodę symboliczną analizy obwodu składa się Przejście z przebiegu czasowego na opis zespolony (symboliczny) dla źródeł prądu i napięcia $u(t)=U_{m}sin(\omega t+{\psi }_u)\to \frac{U_m}{\sqrt{2}}{e}^j{}^{{\psi }_u}$ $i(t)=I_{m}sin(\omega t+{\psi }_i)\to \frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}$ Zastosowanie reprezentacji elementów poprzez ich impedancje zespolone Zastosowanie praw Kirchoffa dla wartości symbolicznych Rozwiązanie układu równań w postaci skutecznej zespolonej Ewentualnie (w miarę potrzeb) przedstawienie rozwiązania w postaci czasowej (odwrotna operacja) do wykonanej w punkcie pierwszym).

---

Wykresy wektorowe obwodu W przypadku analizy obwodów RLC w stanie ustalonym ważnym pojęciem jest wykres wektorowy, zwany również wykresem wskazowym, przedstawiający w sposób orientacyjny zależności między poszczególnymi wektorami prądu i napięcia w obwodzie. Jak wiadomo każdej liczbie zespolonej można przyporządkować reprezentację geometryczną w postaci odpowiedniej zależności wektorowej przedstawionej na płaszczyźnie, w której oś pozioma odpowiada części rzeczywistej a oś pionowa części urojonej liczby zespolonej. Konstruując wykres należy pamiętać, że pomnożenie wektora przez operator $j$ jest równoważne jego obrotowi o kąt 90 stopni przeciwnie do ruchu wskazówek zegara gdyż operator j jest równy $e^j{}^{90^o}$ Podobnie pomnożenie wektora przez operator $-j$ jest równoważne jego obrotowi o kąt 90 stopni zgodnie z ruchem wskazówek zegara gdyż operator -j jest równy $e^{-}{}^j{}^{90^o}$ Pomnożenie wektora przez liczbę rzeczywistą nie zmienia pozycji wektora w przestrzeni o ile jest to liczba dodatnia lub zmienia zwrot wektora o jeśli liczba ta jest ujemna. 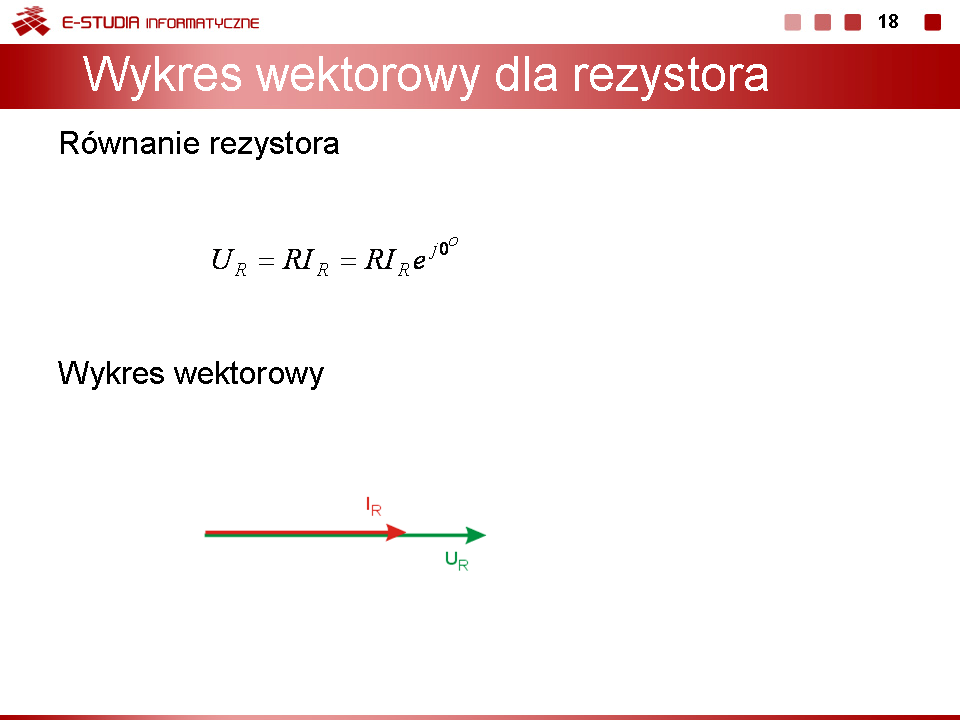Z zależności prądowo-napięciowych dla rezystora jest oczywiste, że $U_R=R{I}_R$ co wobec rzeczywistych, dodatnich wartości R oznacza, że napięcie na rezystorze jest w fazie z prądem tego rezystora. Dla cewki obowiązuje Parser nie mógł rozpoznać (nieznana funkcja „\omeha”): {\displaystyle U_L=j\omeha LI_L} co oznacza, że napięcie na cewce wyprzedza prąd o kąt . Podobnie napięcie na kondensatorze opóźnia się względem swojego prądu o kąt , gdyż $U_C=-j\frac{1}{\omega C}{I}_C$

---