GKIW Moduł 8 - Modelowanie oświetlenia: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
| Linia 88: | Linia 88: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_11.png|thumb|500px]] | ||
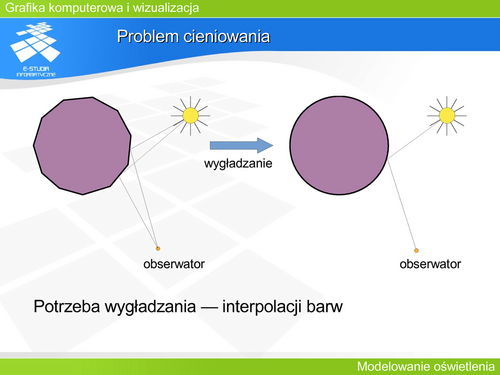
|valign="top"|Prawo Lamberta odnosi się także do odbicia światła od idealnie rozpraszającej powierzchni (powierzchni lambertowskiej). Powierzchnie rzeczywiste odbijają światło zgodnie z prawem Lamberta tylko w pewnym kącie. Dobrym przykładem materiału, którego powierzchnia odbija w przybliżeniu zgodnie z prawem Lamberta jest kreda. | |valign="top"|Prawo Lamberta odnosi się także do odbicia światła od idealnie rozpraszającej powierzchni (powierzchni lambertowskiej). Powierzchnie rzeczywiste odbijają światło zgodnie z prawem Lamberta tylko w pewnym kącie. Dobrym przykładem materiału, którego powierzchnia odbija w przybliżeniu zgodnie z prawem Lamberta jest kreda. | ||
| Linia 95: | Linia 95: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_12.png|thumb|500px]] | ||
|valign="top"|Funkcję BRDF <math>f(\breve{L},\breve{V})</math> definiuje się jako iloraz luminancji obserwowanej z kierunku <math>-\breve{V}</math>, do natężenia napromieniowania światła padającego z kierunku <math>-\breve{L}</math>. Znane funkcje BRDF można podzielić na dwie grupy : zależności opracowane eksperymentalnie i zależności mające podłoże fizyczne. Pierwszą grupę stanowią zależności, których opis matematyczny został eksperymentalnie dobrany do oczekiwanych (lub zmierzonych) efektów. Nie mają one żadnego uzasadnienia teorety¬cznego, ale są dobrą aproksymacją rzeczywistych zjawisk - dają dobre rezultaty. Drugą grupę stanowią opracowania, które powstały na podstawie odpowiedniej teorii fizycznej opisującej gładkość (chropowatość) powierzchni. | |valign="top"|Funkcję BRDF <math>f(\breve{L},\breve{V})</math> definiuje się jako iloraz luminancji obserwowanej z kierunku <math>-\breve{V}</math>, do natężenia napromieniowania światła padającego z kierunku <math>-\breve{L}</math>. Znane funkcje BRDF można podzielić na dwie grupy : zależności opracowane eksperymentalnie i zależności mające podłoże fizyczne. Pierwszą grupę stanowią zależności, których opis matematyczny został eksperymentalnie dobrany do oczekiwanych (lub zmierzonych) efektów. Nie mają one żadnego uzasadnienia teorety¬cznego, ale są dobrą aproksymacją rzeczywistych zjawisk - dają dobre rezultaty. Drugą grupę stanowią opracowania, które powstały na podstawie odpowiedniej teorii fizycznej opisującej gładkość (chropowatość) powierzchni. | ||
|} | |} | ||
| Linia 101: | Linia 101: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_13.png|thumb|500px]] | ||
|valign="top"|Symetryczność funkcji BRDF oznacza, że zamiana obserwatora i źródła światła nie spowodowałaby zmiany opisu zjawiska. To znaczy <math>f(\breve{L},\breve{V})=f(\breve{V},\breve{L})</math>. | |valign="top"|Symetryczność funkcji BRDF oznacza, że zamiana obserwatora i źródła światła nie spowodowałaby zmiany opisu zjawiska. To znaczy <math>f(\breve{L},\breve{V})=f(\breve{V},\breve{L})</math>. | ||
Drugim warunkiem jest zasada zachowania energii, zgodnie z którą suma całkowitej energii wypromieniowanej na skutek odbicia światła od powierzchni jest nie większa niż energia światła padającego. | Drugim warunkiem jest zasada zachowania energii, zgodnie z którą suma całkowitej energii wypromieniowanej na skutek odbicia światła od powierzchni jest nie większa niż energia światła padającego. | ||
| Linia 109: | Linia 109: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_14.png|thumb|500px]] | ||
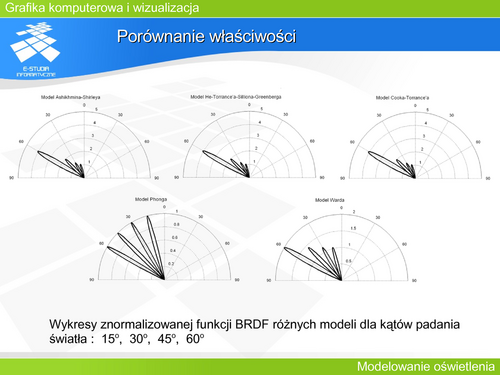
|valign="top"|W literaturze można wskazać wiele prac porównujących, przede wszystkim pod względem obliczeniowym, różne podejścia do opisu zjawiska odbicia. Znane funkcje BRDF można podzielić na dwie grupy : zależności opracowane eksperymentalnie i zależności mające podłoże fizyczne. Pierwszą grupę stanowią zależności, których opis matematyczny został eksperymentalnie dobrany do oczekiwanych (lub zmierzonych) efektów. Nie mają one żadnego uzasadnienia teoretycznego, ale są dobrą aproksymacją rzeczywistych zjawisk. Drugą grupę stanowią opracowania, które powstały na podstawie odpowiedniej teorii fizycznej opisującej gładkość (chropowatość) powierzchni. Obie jednak grupy są pewnym przybliżeniem rzeczywistości. Natomiast ze względów praktycznych nie zawsze jest celowe korzystanie z funkcji BRDF powstałych na podstawie pomiarów rzeczywistej powierzchni, gdyż jest to bardzo kosztowne obliczeniowo. Nawet w takich przypadkach stosuje się pewne aproksymacje . Warto więc zastanowić się nad wyborem odpowiedniej funkcji BRDF. Szczególnie jest to istotne w sytuacji prowadzenia obliczeń z wykorzystaniem gotowych pakietów numerycznych gdzie wybór dostępnych parametrów może być ograniczony. | |valign="top"|W literaturze można wskazać wiele prac porównujących, przede wszystkim pod względem obliczeniowym, różne podejścia do opisu zjawiska odbicia. Znane funkcje BRDF można podzielić na dwie grupy : zależności opracowane eksperymentalnie i zależności mające podłoże fizyczne. Pierwszą grupę stanowią zależności, których opis matematyczny został eksperymentalnie dobrany do oczekiwanych (lub zmierzonych) efektów. Nie mają one żadnego uzasadnienia teoretycznego, ale są dobrą aproksymacją rzeczywistych zjawisk. Drugą grupę stanowią opracowania, które powstały na podstawie odpowiedniej teorii fizycznej opisującej gładkość (chropowatość) powierzchni. Obie jednak grupy są pewnym przybliżeniem rzeczywistości. Natomiast ze względów praktycznych nie zawsze jest celowe korzystanie z funkcji BRDF powstałych na podstawie pomiarów rzeczywistej powierzchni, gdyż jest to bardzo kosztowne obliczeniowo. Nawet w takich przypadkach stosuje się pewne aproksymacje . Warto więc zastanowić się nad wyborem odpowiedniej funkcji BRDF. Szczególnie jest to istotne w sytuacji prowadzenia obliczeń z wykorzystaniem gotowych pakietów numerycznych gdzie wybór dostępnych parametrów może być ograniczony. | ||
|} | |} | ||
| Linia 115: | Linia 115: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_15.png|thumb|500px]] | ||
|valign="top"|Zaproponowany przez Cooka i Torrance’a w 1981 roku na podstawie wcześniejszych prac Torrance’a i Sparrowa. Model Cooka-Torrance’a jest modelem uzasadnionym fizycznie, spełniającym zasadę wzajemności i zasadę zachowania energii, chociaż znane są w literaturze rozważania wskazujące na pewne problemy, które mogą się pojawić dla kątów padania promienia bliskich kątowi prostemu. | |valign="top"|Zaproponowany przez Cooka i Torrance’a w 1981 roku na podstawie wcześniejszych prac Torrance’a i Sparrowa. Model Cooka-Torrance’a jest modelem uzasadnionym fizycznie, spełniającym zasadę wzajemności i zasadę zachowania energii, chociaż znane są w literaturze rozważania wskazujące na pewne problemy, które mogą się pojawić dla kątów padania promienia bliskich kątowi prostemu. | ||
Znane jest również uproszczenie modelu Cooka-Torance’a - model Schlicka, zaproponowany w 1994 roku. Autor starał się dokonać uproszczenia z zachowaniem fizycznego charakteru modelu pierwotnego, ale znacznie podnieść atrakcyjność obliczeniową. W modelu Cooka-Torrance’a w równaniu zastąpione zostały wielkości G i D (funkcja rozkładu Beckmanna) prostszymi funkcjami wymiernymi. | Znane jest również uproszczenie modelu Cooka-Torance’a - model Schlicka, zaproponowany w 1994 roku. Autor starał się dokonać uproszczenia z zachowaniem fizycznego charakteru modelu pierwotnego, ale znacznie podnieść atrakcyjność obliczeniową. W modelu Cooka-Torrance’a w równaniu zastąpione zostały wielkości G i D (funkcja rozkładu Beckmanna) prostszymi funkcjami wymiernymi. | ||
| Linia 123: | Linia 123: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_16.png|thumb|500px]] | ||
|valign="top"|G opisuje tłumienie geometryczne. W modelu Cooka-Torrance’a założono, że powierzchnia materiału jest wielościanem złożonym z mikroelementów (mikroluster). Ich rozmiary i rozkład położeń decydują o chropowatości lub gładkości powierzchni. Przyjęto, że powierzchnia pokryta jest wgłębieniami typu V – to znaczy są to wgłębienia o kształcie ostrosłupa. Tłumienie geometryczne jest wzajemnym zasłanianiem mikroelementów powierzchni i jest opisane podaną zależnością. | |valign="top"|G opisuje tłumienie geometryczne. W modelu Cooka-Torrance’a założono, że powierzchnia materiału jest wielościanem złożonym z mikroelementów (mikroluster). Ich rozmiary i rozkład położeń decydują o chropowatości lub gładkości powierzchni. Przyjęto, że powierzchnia pokryta jest wgłębieniami typu V – to znaczy są to wgłębienia o kształcie ostrosłupa. Tłumienie geometryczne jest wzajemnym zasłanianiem mikroelementów powierzchni i jest opisane podaną zależnością. | ||
| Linia 130: | Linia 130: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_17.png|thumb|500px]] | ||
|valign="top"|D jest funkcją rozkładu mikroelementów tworzących powierzchnię. Cook i Torrance zaproponowali użycie funkcji rozkładu Beckmanna jako najbardziej odpowiadającej wielościennemu charakterowi powierzchni dla różnych materiałów. | |valign="top"|D jest funkcją rozkładu mikroelementów tworzących powierzchnię. Cook i Torrance zaproponowali użycie funkcji rozkładu Beckmanna jako najbardziej odpowiadającej wielościennemu charakterowi powierzchni dla różnych materiałów. | ||
| Linia 137: | Linia 137: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_18.png|thumb|500px]] | ||
|valign="top"|O właściwościach kierunkowego odbicia w przyjętym modelu decyduje funkcja D rozkładu mikropowierzchni (czasami nazywana funkcją dystrybucji). D jest najczęściej funkcją kąta <math>\beta</math> (kąta <math>\alpha</math> w przypadku modelu Phonga). Spełnienie zasady zachowania energii wymaga, aby funkcja dystrybucji spełniała warunek normalizacji. Oznacza to dla powierzchni izotropowych następującą zależność: | |valign="top"|O właściwościach kierunkowego odbicia w przyjętym modelu decyduje funkcja D rozkładu mikropowierzchni (czasami nazywana funkcją dystrybucji). D jest najczęściej funkcją kąta <math>\beta</math> (kąta <math>\alpha</math> w przypadku modelu Phonga). Spełnienie zasady zachowania energii wymaga, aby funkcja dystrybucji spełniała warunek normalizacji. Oznacza to dla powierzchni izotropowych następującą zależność: | ||
| Linia 150: | Linia 150: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_19.png|thumb|500px]] | ||
|valign="top"|Współczynnik Fresnela opisuje zależność odbicia światła od kąta padania i długości fali. Określa stosunek energii światła odbitego do energii światła padającego. Warto pamiętać, że kształt zależności kątowych tego współczynnika zależy od długości fali oraz polaryzacji światła. Prezentowane wykresy pokazują wartości średnie światła niespolaryzowanego. | |valign="top"|Współczynnik Fresnela opisuje zależność odbicia światła od kąta padania i długości fali. Określa stosunek energii światła odbitego do energii światła padającego. Warto pamiętać, że kształt zależności kątowych tego współczynnika zależy od długości fali oraz polaryzacji światła. Prezentowane wykresy pokazują wartości średnie światła niespolaryzowanego. | ||
Schlick zaproponował dobrą aproksymację tej funkcji (według autora aproksymacji błąd mniejszy niż 1%). Opisuje ją wielomianowa funkcja kąta i wartość współczynnika <math>F_0</math> dla zerowego kąta i określonej długości fali. Wartości <math>F_0</math> są podawane przez tablice materiałowe. | Schlick zaproponował dobrą aproksymację tej funkcji (według autora aproksymacji błąd mniejszy niż 1%). Opisuje ją wielomianowa funkcja kąta i wartość współczynnika <math>F_0</math> dla zerowego kąta i określonej długości fali. Wartości <math>F_0</math> są podawane przez tablice materiałowe. | ||
| Linia 158: | Linia 158: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd_20.png|thumb|500px]] | ||
|valign="top"|Model Warda zaproponowany w 1992 roku uwzględniający anizotropię odbicia – równanie. Jest to jeden z pierwszych tego typu modeli i jednocześnie jest on często używany nadal. Model ten jest często dostępny w gotowych pakietach oprogramowania. | |valign="top"|Model Warda zaproponowany w 1992 roku uwzględniający anizotropię odbicia – równanie. Jest to jeden z pierwszych tego typu modeli i jednocześnie jest on często używany nadal. Model ten jest często dostępny w gotowych pakietach oprogramowania. | ||
Model Warda niestety nie uwzględnia współczynnika Fresnela, co nie daje możliwości opisania w pełni właściwości materiałowych i uwzględnienia zależności kątowych. Jest to szczególnie widoczne dla dużych kątów padania światła. | Model Warda niestety nie uwzględnia współczynnika Fresnela, co nie daje możliwości opisania w pełni właściwości materiałowych i uwzględnienia zależności kątowych. Jest to szczególnie widoczne dla dużych kątów padania światła. | ||
Wersja z 10:46, 22 lut 2007
Wykład
 |
 |
 |
 |
Literatura
 |