Wersja z 13:59, 16 sty 2007

Wykład

W poprzednim module zajmowaliśmy się falą płaską rozchodzącą się w nieograniczonej przestrzeni, która jest ważnym rodzajem fali elektromagnetycznej w zastosowaniach telekomunikacyjnych bo występuje pomiędzy antenami nadawczą i odbiorczą.

Niemniej istotne jest rozchodzenie się fal elektromagnetycznych we wszelkiego rodzaju liniach transmisyjnych, w których fale prowadzone są w określonym kierunku. Linie te nazywamy prowadnicami falowymi.

W module 3 poznamy fale elektromagnetyczne w podstawowych prowadnicach falowych stosowanych w technice pasm radiowych i mikrofalowych. Przedstawimy własności i parametry tych fal podkreślając różnice z falą płaską. Wprowadzimy podstawowe parametry obwodowe prowadnicy falowej (napięcie, prąd, impedancję charakterystyczną), które będą przydatne w szeregu zagadnieniach omawianych w kolejnych wykładach.

Rozpoczniemy od klasyfikacji fal elektromagnetycznych ze wskazaniem prowadnic falowych, w których się rozchodzą.

Ponieważ w strukturze prowadnicy występują dielektryki i przewodniki, należy omówić warunki brzegowe pól na granicy tych ośrodków. Znajomość tych warunków jest niezwykle istotna przy wyznaczaniu pól elektromagnetycznych w prowadnicach falowych.

W dalszej części przedstawione zostaną podstawowe prowadnice falowe stosowane do transmisji sygnałów na odległości od ułamka metra do setek metrów w zakresie fal radiowych i mikrofalowych, czyli linia współosiowa oraz falowody prostokątny i kołowy. Poznamy struktury tych linii, własności fal w nich propagowanych, rozkłady pól elektromagnetycznych podstawowych rodzajów i parametry obwodowe linii.

Podzespoły pracujące w pasmach mikrofalowych i stosowane w systemach radiokomunikacji realizowane są powszechnie jako mikrofalowe układy scalone (w skrócie: MUS). Charakterystyczną cechą tych układów jest występowanie prowadnicy falowej pomiędzy elementami o stałych skupionych (diody, tranzystory, rezystory, kondensatory). Poznamy dwie podstawowe prowadnice MUS: linię mikropaskową i falowód koplanarny.

Dla celów analizy prowadnic falowych przyjmuje się, że występujące w nich przewodniki są idealne. To założenie znakomicie upraszcza proces wyznaczania pola elektromagnetycznego w linii, ale nie pozwala na obliczenie tłumienia fali. Rzeczywiste przewodniki są istotnym źródłem strat mocy fali. Z punktu widzenia transmisji sygnałów tłumienie fali w prowadnicy jest ważnym zjawiskiem i zajmiemy się nim na zakończenie tego modułu.

Prowadzenie fal uzyskuje się wzdłuż określonego układu przewodników lub dielektryków (tzn. w obszarach cylindrycznych, których granicę są przewodzące lub są to granice dwóch dielektryków, ewentualnie odpowiednia kombinacja wymienionych materiałów). W przypadku prowadzenia fal wzdłuż przewodników, możliwe jest rozchodzenie się energii elektromagnetycznej w liniach składających się z dwóch lub więcej przewodów, a także w rurach (najczęściej o przekroju prostokątnym albo kołowym), które nie zawierają wewnątrz dodatkowych przewodników, tzw. falowodach. Natomiast przykładem prowadnicy falowej będącej układem warstw dielektrycznych jest światłowód, bez którego trudno wyobrazić sobie dzisiejszą telekomunikację.

Fale w prowadnicach falowych nie muszą być falami typu TEM, tzn. mogą one mieć składowe pól elektrycznego i magnetycznego wzdłuż kierunku rozchodzenia się fali. Wprowadzić należy klasyfikację możliwych rodzajów fal nazywanych również modami.

Przyjmijmy, że fala rozchodzi się zgodnie z kierunkiem osi z i wtedy wyróżnia się następujące typy fal:

fala typu TEM (poprzeczna elektryczna-magnetyczna, z ang. Transverse Electric-Magnetic):

E_{z} = 0

– pole elektryczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali (wektor natężenia pola elektrycznego ma co najwyżej dwie składowe),

H_{z} = 0

– pole magnetyczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali(wektor natężenia pola magnetycznego ma co najwyżej dwie składowe);

fala typu E (określana też TM – poprzeczna magnetyczna, z ang. Transverse Magnetic):

E_{z} \neq 0

– niezerowa składowa pola elektrycznego w kierunku rozchodzenia się fali (może mieć trzy składowe),

H_{z} = 0

– pole magnetyczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali;

fala typu H (określana też TE – poprzeczna elektryczna, z ang. Transverse Electric):

H_{z} \neq 0

– niezerowa składowa pola magnetycznego w kierunku rozchodzenia się fali (może mieć trzy składowe),

E_{z} = 0

– pole elektryczne leży w płaszczyźnie prostopadłej do kierunku propagacji fali;

fala typu EH: $E_{z} \neq 0$ , $H_{z} \neq 0$ .

Z powyższego wykazu wynika, że tylko pierwszy z wymienionych typów fal jest falą poprzeczną. Prowadnice falowe, w których mogą rozchodzić się rodzaje TEM nazywamy liniami TEM lub prowadnicami TEM. Struktura prowadnicy TEM musi zawierać co najmniej dwa przewody. Przykładem linii TEM jest linia współosiowa, tzw. kabel koncentryczny.

Fale E i H rozchodzą się w falowodach. Falowody stosuje się do prowadzenia fali elektro-magnetycznej z mniejszymi stratami niż w linii TEM (np. w transponderach satelitów telekomunikacyjnych) lub do przesyłania dużych mocy, których przesłanie nie jest możliwe linią współosiową (np. w radarach).

Fale typu EH występują między innymi w falowodach dielektrycznych i światłowodach.

Określenie postaci fali elektromagnetycznej w prowadnicy falowej wiąże się z poszukiwaniem rozwiązań równań Maxwella, które jest zagadnieniem matematycznym innego typu niż w przypadku fali w nieograniczonej przestrzeni. Ze względu na to, że mamy tu do czynienia z obszarem cylindrycznym o granicy przewodzącej lub w formie granicy dwóch dielektryków, musimy teraz uwzględnić warunki brzegowe. W konsekwencji pewne własności fal elektromagnetycznych w prowadnicach są inne niż fali płaskiej.

Pola elektryczne i magnetyczne w otoczeniu obustronnym granicy ośrodków muszą spełniać równania Maxwella, muszą więc być spełnione pewne wzajemne relacje między polami po obu stronach granicy ośrodków oraz występującymi na granicy prądami i ładunkami elektrycznymi. Relacje te nazywamy warunkami brzegowymi i można wyprowadzić je z równań Maxwella.

Na rysunku przedstawiono pola, prąd i ładunek, które rozpatruje się w warunkach brzegowych. Wszystkie te wielkości mogą, w ogólnym przypadku, występować w jednym punkcie granicznym. Pokazana na rysunku granica jest takim „rozciągniętym punktem”. Parametry obu ośrodków są liczbami, czyli są one liniowe, jednorodne i izotropowe.

W ośrodku 1, w pewnym punkcie na granicy z ośrodkiem 2, występuje pole elektryczne i związene z nim wektory ${\vec{D}}_{1} = ε_{1} {\vec{E}}_{1}$ oraz pole magnetyczne i wektory ${\vec{B}}_{1} = μ_{1} {\vec{H}}_{1}$ . W tym samym punkcie granicznym w ośrodku 2 mamy pola ${\vec{D}}_{2} = ε_{2} {\vec{E}}_{2}$ i ${\vec{B}}_{2} = μ_{2} {\vec{H}}_{2}$ . Przyjmijmy również, że w omawianym punkcie płaszczyzny rozgraniczającej ośrodki może występować wektor gęstości prądu powierzchniowego ${\vec{J}}_{s}$ , którego miarą jest Amper na metr [A/m], oraz istnieje ładunek o gęstości powierzchniowej $ρ_{s} [C / m^{2}]$ .

Należy zauważyć, że dowolny wektor pola elektrycznego w ośrodku 1 można przedstawić w dowolnym punkcie na granicy jako sumę wektorową składowej stycznej $E_{t 1}$ oraz składowej normalnej $E_{n 1}$ do granicy rozdziału ośrodków. Analogicznie wyraża się pozostałe wektory w ośrodku 1, czyli ${\vec{D}}_{1}$ , ${\vec{H}}_{1}$ , ${\vec{B}}_{1}$ oraz pola w ośrodku 2, co schematycznie ilustruje rysunek (na tym rysunku zaznaczono tylko składowe istotne dla warunków brzegowych oraz wersor $\vec{n}$ normalny do granicy ośrodków).

Sformułujmy warunki, które spełniają pola elektryczne i magnetyczne na granicy dwóch ośrodków.

Warunki brzegowe dla pola elektrycznego:

$E_{t 2} = E_{t 1}$ – składowa styczna wektora natężenia pola elektrycznego jest ciągła na granicy dwóch ośrodków;
$D_{n 2} - D_{n 1} = ρ_{s}$ – składowa normalna wektora indukcji elektrycznej jest ciągła na granicy dwóch ośrodków z wyjątkiem przypadku, gdy na granicy istnieje ładunek powierzchniowy i wtedy doznaje ona skokowej zmiany o wartość gęstości powierzchniowej ładunku.

Warunki brzegowe dla pola magnetycznego:

$| H_{t 2} - H_{t 1} | = | J_{s} |$ – składowa styczna wektora natężenia pola magnetycznego jest ciągła z wyjątkiem przypadku, gdy na powierzchni granicznej występuje prąd. W tym ostatnim przypadku składowa styczna natężenia pola magnetycznego zmienia skokowo wartość na granicy ośrodków o wartość gęstości prądu powierzchniowego;
$B_{n 2} = B_{n 1}$ – składowa normalna wektora indukcji magnetycznej jest na granicy dwóch ośrodków ciągła, bo nie występują odosobnione ładunki magnetyczne.

Warto zaznaczyć, że przedstawione warunki brzegowe obowiązują tak dla pól statycznych jak i dla pól zmiennych w czasie.

W wielu zagadnieniach występujących w technice mikrofalowej mamy do czynienia z układem dwóch dielektryków bądź ze strukturą dielektryk – przewodnik. Rozważmy zachowanie pola elektromagnetycznego w tych szczególnych przypadkach.

Na granicy miedzy dwoma bezstratnymi dielektrykami nie występuje ładunek powierzchniowy oraz nie płynie prąd przewodzenia.

Warunki brzegowe podaje się z reguły w formie iloczynów wektorowych i skalarnych, tak jak pokazano na slajdzie. W każdym iloczynie występuje wersor normalny do granicy rozdziału ośrodków. Z własności iloczynu wektorowego wynika, że zawiera on informacje tylko o składowych wektorów pól stycznych do granicy ośrodków, ponieważ iloczyn wektorowy wersora $\vec{n}$ i wektora do niego równoległego (składowa normalna pola) jest tożsamościowo równy zeru. Analogicznie, iloczyn skalarny pozwala tylko na wnioski dotyczące składowych wektorów pól normalnych do powierzchni rozdzielającej ośrodki.

Podane równania wektorowe i wynikające z nich równania skalarne stwierdzają, że składowe styczne wektorów $\vec{E}$ i $\vec{H}$ oraz składowe normalne wektorów $\vec{D}$ i $\vec{B}$ są ciągłe na granicy dielektryków. Można wykazać, że spełnienie warunków brzegowych dla składowych stycznych na granicy dwóch ośrodków dielektrycznych pociąga za sobą automatycznie spełnienie warunków ciągłości dla składowych normalnych.

Podany na slajdzie przykład ilustruje zachowanie się pól na granicy dwóch dielektryków. Wektor natężenia pola magnetycznego nie ulega zmianie przy przejściu z jednego ośrodka do drugiego. Natomiast wektory natężenia pola elektrycznego w obu ośrodkach różnią się, tak co do wartości jak i kierunku.

W liniach transmisyjnych powszechnie występuje granica między dielektrykiem i dobrym przewodnikiem, który często można uznać za idealny. Rozważmy warunki brzegowe dla pól zmiennych w czasie panujące na granicy dielektryka (ośrodek 2) i idealnego przewodnika (ośrodek 1).

W idealnym przewodniku $(σ = \infty)$ pole elektryczne musi być równe zeru, gdyż w przeciwnym przypadku wywoływałoby prąd przewodzenia o nieskończonym natężeniu $\vec{J} = σ \vec{E}$ . Istnienie w tym ośrodku zmiennego pola magnetycznego jest również niemożliwe, ponieważ zgodnie z pierwszym prawem Maxwella musiałoby wywołać pole elektryczne, co byłoby sprzeczne z poprzednim stwierdzeniem.

Z podanych na slajdzie równań dotyczących pola elektrycznego wynika, że:

składowa styczna wektora natężenia pola elektrycznego na granicy idealnego przewodnika jest równa zeru, a więc pole elektryczne musi być prostopadłe do powierzchni przewodnika;
pole elektryczne indukuje na powierzchni przewodnika powierzchniowy ładunek elektryczny o gęstości równej wartości indukcji elektrycznej.

Z kolei własności pola magnetycznego na granicy dielektryka z idealnym przewodnikiem są następujące:

składowa normalna wektora indukcji magnetycznej jest zerowa na brzegu idealnego przewodnika, czyli pole magnetyczne musi być styczne do granicy przewodnika;
pole magnetyczne wywołuje na jego powierzchni prąd przewodzenia o gęstości równej wartości natężenia pola magnetycznego. Kierunek wektora gęstości prądu jest prostopadły do wektora natężenia pola magnetycznego, a jego zwrot jest taki, że wektory $\vec{n}$ , ${\vec{H}}_{2}$ , ${\vec{J}}_{s}$ tworzą prawoskrętną trójkę wektorów.

Rysunek na slajdzie pokazuje istotne wielkości występujące na granicy dielektryk – idealny przewodnik. Trzeba podkreślić, że pola są zmienne w czasie i w każdej chwili spełnione są warunki brzegowe. Oznacza to, że w takt zmian pól zmieniają się gęstość powierzchniowa ładunku i gęstość prądu powierzchniowego.

Przypomnijmy, że prowadnica TEM musi zawierać co najmniej dwa przewody. Rysunek przedstawia przekrój poprzeczny przykładowej prowadnicy TEM mającej trzy idealne przewodniki i wypełnionej dielektrykiem stratnym.

Wektory pól elektrycznego i magnetycznego fali typu TEM mają tylko składowe poprzeczne do osi propagacji fali. Można wykazać, że zależności tych pól w prowadnicy TEM wzdłuż kierunku rozchodzenia się fali, czyli od zmiennej z, są identyczne jak dla fali płaskiej w przestrzeni nieograniczonej i dla fali rozchodzącej się w kierunku +0z opisuje je czynnik Parser nie mógł rozpoznać (błąd składni): {\displaystyle exp(–\gamma z)} , przy czym $γ$ to współczynnik propagacji.

Zasadnicza różnica między cechami pół fali płaskiej i pól w linii TEM jest związana z tym, że pola w ośrodku nieograniczonym nie zależą od zmiennych w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali, natomiast w prowadnicy TEM, w której muszą być spełnione określone warunki brzegowe na powierzchni przewodników linii, pola na ogół zależą od tych zmiennych. Wektory pól elektrycznego i magnetycznego zależne od zmiennych x, y i występujące w płaszczyźnie z = 0 oznaczono indeksem T. Pokazane na slajdzie ogólne zależności dla pól w linii TEM są matematycznym zapisem zgodnym z powyższymi stwierdzeniami.

Współczynnik propagacji fali w linii TEM jest taki sam jak dla fali płaskiej w nieograniczonym ośrodku i o jego wartości decydują pulsacja oraz parametry materiału wypełniającego prowadnicę falową. W konsekwencji własności propagacyjne fali typu TEM są takie jak fali płaskiej.

W prowadnicach falowych stosuje się małostratne dielektryki gdyż tylko takie wypełnienie linii pozwala na przesyłanie fali z akceptowanymi stratami. Do obliczenia wspólczynników tłumienia i fazy fali stosujemy przybliżone wyrażenia pokazane na slajdzie. Pamiętać należy, że stosując te przybliżenia zaniedbujemy dyspersję prowadnicy TEM wynikającą ze strat, gdyż według przybliżenia współczynnik fazy liniowo zależy od częstotliwości. Uwzględnione zostaje tłumienie fali w trakcie propagacji i warto zapamiętać, że wzrasta ono liniowo z pulsacją.

Znając wyrażenie określające współczynnik fazy możemy wyznaczyć prędkości fazową i grupową fali TEM. Prędkość fazowa jest równa ilorazowi pulsacji przez współczynnik fazy, z kolei wartość prędkości grupowej określa pochodna pulsacji względem współczynnika fazy. Dla fali typu TEM w prowadnicy, dla której przyjmujemy liniowy wzrost współczynnika fazy z częstotliwością, prędkości fazowa i grupowa nie zależą od częstotliwości i mają tę samą wartość równą prędkości światła w dielektryku wypełniającym linię.

Własnością fali typu TEM jest prostopadłość wektorów natężeń pól elektrycznego i magnetycznego. Iloczyny wektorowe pokazane na slajdzie ujmują wzajemne powiązanie pól ze sobą i wersorem wskazującym kierunek rozchodzenia się fali. Równania te pozwalają wyznaczyć jedno z pól gdy znamy drugie. Zapisano w równaniach pola zależne tylko od współrzędnych x i y bo czynnik Parser nie mógł rozpoznać (błąd składni): {\displaystyle exp(–\gamma z)} występował po obu stronach równości i uległ redukcji. Współczynnikiem proporcjonalności między natężeniem pola elektrycznego i natężeniem pola magnetycznego fali typu TEM jest impedancja właściwa dielektryka – tak również jest dla fali płaskiej.

Impedancja właściwa stratnego dielektryka jest wielkością zespoloną, której moduł i argument zależą, poza parametrami ośrodka, od częstotliwości. Dla impedancji właściwej dielektryka małostratnego stosuje się przybliżone zależności określające jej moduł i argument. Widzimy, że moduł impedancji wyraża się w przybliżeniu taką samą zależnością jak dla dielektryka bezstratnego i nie zależy od konduktywności ośrodka oraz częstotliwości fali. Argument impedancji, który jest równocześnie przesunięciem fazy między natężeniami pól elektrycznego i magnetycznego, jest równy połowie kąta stratności.

Przypomnijmy, że jednym z parametrów charakteryzujących falę elektromagnetyczną jest impedancja falowa, którą definiujemy jako stosunek wartości wzajemnie prostopadłych składowych wektorów natężeń pól elektrycznego i magnetycznego. Dodatkowo składowe te muszą być prostopadłe do kierunku rozchodzenia się fali. Ten ostatni warunek jest a priori spełniony dla fali typu TEM.

Zauważmy, że we wzorze wyrażającym impedancję falową znak minus występuje tylko przed ilorazem składowych $E_{y}$ i $H_{y}$ . Zasadność istnienia przeciwnych znaków przed ilorazami odpowiednich składowych pól można wyjaśnić korzystając z podanych związków między polami. Przyjmując, że fala TEM rozchodzi się w kierunku +0z i zapisując wektor natężenia pola elektrycznego fali TEM jako ${\vec{E}}_{T} = {\vec{i}}_{x} E_{x} + {\vec{i}}_{y} E_{y}$ otrzymamy to wektor natężenia pola magnetycznego w formie ${\vec{H}}_{T} = {\vec{i}}_{y} H_{y} + {\vec{i}}_{y} H_{y} = - {\vec{i}}_{x} \frac{E_{y}}{Z} + {\vec{i}}_{y} \frac{E_{x}}{Z}$ .

Z powyższych postaci pól widać, że należy umieścić znak minus w definicji impedancji falowej.

Dla fali typu TEM, tak jak dla fali płaskiej, impedancja falowa równa jest impedancji właściwej ośrodka.

Na slajdzie zapisano pierwsze równanie Maxwella dla fali TEM rozdzielając operator nabla

(\nabla)

na część poprzeczną

(\nabla_{T})

i wzdłużną

(\nabla_{z})

względem kierunku rozchodzenia się fali. Wiemy, że wektor natężenia pola elektrycznego ma tylko składowe prostopadłe do osi 0z. Rotacja w płaszczyźnie xy tego wektora musi być wektorem mającym tylko składową z. Jednak wektor natężenia pola magnetycznego z prawej strony równania Maxwella ma tylko składowe x i y. Zatem rotacja w płaszczyźnie poprzecznej wektora natężenia pola elektrycznego fali typu TEM musi być równa zeru. W ten prosty sposób wykazaliśmy, że pole elektryczne omawianej fali w płaszczyźnie poprzecznej do kierunku propagacji jest bezwirowe. Podobnie postępując z drugim równaniem Maxwella stwierdzimy, że taką samą własność ma pole magnetyczne. Należy jeszcze raz zaznaczyć, że pola fali TEM są bezwirowe tylko w płaszczyźnie z = constans, czyli wtedy gdy nie są funkcjami zmiennej z.

Dla bezwirowego pola wektorowego możemy zdefiniować skalarną funkcję nazywaną potencjałem skalarnym. Wprowadzenie potencjału nie jest konieczne z fizycznego punktu widzenia, ale jest on pomocny w uproszczeniu rozważań matematycznych w szeregu zagadnieniach. Pojęcie potencjału elektrycznego powszechnie jest znane z kursu elektrostatyki.

Równanie przedstawione na slajdzie jest definicją potencjału elektrycznego i dla rozważanego przypadku stwierdza, że bezwirowe pole elektryczne fali typu TEM powiązane jest z potencjałem elektrycznym V w taki sposób, że wektor natężenia tego pola jest równy gradientowi potencjału V ze znakiem minus.

W obszarze dielektryka wypełniającego prowadnicę TEM nie ma zgromadzonych ładunków. Trzecie równanie Maxwella (prawo Gaussa dla pola elektrycznego) wskazuje, że pole elektryczne fali typu TEM jest bezźródłowe. Zastępując w tym równaniu wektor natężenia pola elektrycznego przez

- \nabla V

otrzymujemy dwuwymiarowe cząstkowe równanie różniczkowe drugiego rzędu względem potencjału, tzw. równanie Laplace’a.

Przewodniki występujące w strukturze linii TEM formują w przekroju poprzecznym kontury ekwipotencjalne. Potencjały występujące na przewodach stanowią warunki brzegowe dla równania Laplace’a.

Zauważmy, że dla prowadnicy TEM rozwiązywanie układu równań Maxwella sprowadza się do znalezienia rozwiązania dwuwymiarowego równania Laplace’a przy danych wartościach potencjału na brzegach obszaru linii. Po określeniu rozkładu potencjału w przekroju poprzecznym prowadnicy obliczamy wektor natężenia pola elektrycznego, a następnie wektor natężenia pola magnetycznego.

Podsumowując własności fali typu TEM stwierdzamy, że dla takiej fali współczynnik propagacji, długość fali, prędkości fazowa i grupowa oraz impedancja falowa są takie jak dla fali płaskiej. Natomiast rozkłady pól elektrycznego i magnetycznego zależą od struktury prowadnicy TEM i potencjałów panujących na jej przewodach.

Rozważmy linię współosiową o promieniach a, b (a > b) wypełnioną bezstratnym dielektrykiem o parametrach

ε

,

μ_{0}

i o doskonale przewodzących ściankach, której przekrój poprzeczny ilustruje rysunek. Przewód wewnętrzny linii ma potencjał

V_{0}

, a potencjał przewodu zewnętrznego wynosi zero. W linii tej rozchodzi się fala TEM o pulsacji

ω

w kierunku dodatnim osi 0z.

Linia współosiowa jest strukturą osiowo symetryczną i dogodnie jest zastosować cylindryczny układ współrzędnych, w którym pola fali zależą tylko od dwóch zmiennych $ρ$ , z.

Poszukiwanie pola elektromagnetycznego w linii rozpoczynamy od znalezienia potencjału elektrycznego w przekroju poprzecznym prowadnicy, który spełnia jednowymiarowe równanie Laplace’a w układzie współrzędnych cylindrycznych (potencjał jest rzeczywistą funkcją tylko zmiennej $ρ$ ). Wyrażenie opisujące potencjał to rozwiązanie tego równania, które jest wynikiem dwukrotnego obustronnego jego całkowania z uwzględnieniem potencjałów na przewodach linii. W obszarze dielektryka potencjał maleje logarytmicznie w miarę odsuwania się od przewodu wewnetrznego, na którym ma wartość $V_{0}$ , by osiągnąć wartość zero na przewodzie zewnętrznym.

Znając potencjał, obliczenie wektorów pola elektromagnetycznego jest prostym zagadnieniem.

Gradient potencjału, a tym samym i wektor natężenia pola elektrycznego w linii współosiowej ma tylko składową $ρ$ , która jest prostopadła do powierzchni przewodzących. Zwróćmy uwagę, że zgodnie z warunkami brzegowymi pole elektryczne musi być normalne do powierzchni idealnego przewodnika i spełnienie tego warunku zapewnia w linii współosiowej tylko składowa $ρ$ . Obliczając pochodną potencjału względem zmiennej $ρ$ i uwzględniając znak minus otrzymujemy prostą zależność opisującą rozkład pola elektrycznego w przekroju poprzecznym linii $(E_{T})$ . Wynika, z niej, że natężenie pola elektrycznego w przekroju poprzecznym prowadnicy jest maksymalne przy przewodzie wewnętrznym $(E_{0})$ , maleje ze wzrostem $ρ$ i na granicy z przewodem zewnętrznym wynosi $E_{0} b / a$ . Mnożąc wektor ${\vec{E}}_{T}$ przez czynnik Parser nie mógł rozpoznać (błąd składni): {\displaystyle exp(–j\beta z)} otrzymujemy zespolony wektor nateżenia pola elektrycznego dla fali TEM w linii współosiowej.

Zespolony wektor natężenia pola magnetycznego dla omawianej fali wyznaczamy korzystając z zależności $\vec{H} = Z^{- 1} {\vec{i}}_{z} \times \vec{E}$ . Wektor ten ma jedynie składową $φ$ i jej występowanie powoduje, że spełniony jest warunek brzegowy na granicy dielektryk – idealny przewodnik stwierdzający, że pole magnetyczne na tej granicy musi być styczne do przewodnika. Zależność wartości natężenia pola magnetycznego od promienia $(ρ)$ jest taka jak pola elektrycznego.

Impedancja falowa, czyli stosunek wartości natężeń pól elektrycznego i magnetycznego w każdym punkcie dielektryka w przekroju poprzecznym linii współosiowej ma tę samą wartość równą impedancji właściwej ośrodka.

Wektory rzeczywiste natężeń pól elektrycznego i magnetycznego uzyskujemy mnożąc odpowiednie wektory zespolone przez $e x p (j ω t)$ i wyznaczając części rzeczywiste tych nowo-powstałych wektorów.

Rysunek ilustruje pole elektromagnetyczne w linii współosiowej fali TEM rozchodzącej się w kierunku +0z w chwili t = 0. Pola są w fazie, czyli zmieniają tak samo wzdłuż kierunku propagacji, według funkcji

c o s (β z)

. W płaszczyźnie przekroju poprzecznego wartości pól są największe przy przewodzie wewnętrznym i maleją przy odsuwaniu się od tego przewodu.

Zgodnie z warunkami brzegowymi na granicy dielektryk – przewodnik, ze sładową normalną pola elektrycznego związane są powierzchniowe ładunki elektryczne, a ze składową styczną pola magnetycznego prądy powierzchniowe.

Pole elektryczne indukuje ładunek powierzchniowy na przewodnikach linii, którego wartość gęstości jest równa indukcji elektrycznej. W pokazanym przekroju poprzecznym dla $z = λ / 2$ , na przewodzie zewnętrznym występuje ładunek dodatni, a ładunek ujemny indukowany jest na przewodzie wewnętrznym. Całkowite ładunki zgromadzone na przewodach są równe co do wartości, czyli suma ładunków w przekroju poprzecznym jest równa zeru.

Pole magnetyczne wywołuje prąd powierzchniowy na obu przewodach prowadnicy, a wartość gęstości tego prądu jest równa wartości natężenia pola magnetycznego. We wspomnianym przekroju poprzecznym prąd powierzchniowy na przewodzie wewnętrznym płynie w kierunku –0z, podczas gdy prąd na przewodzie zewnętrznym płynie w kierunku przeciwnym. Analogicznie do ładunków, w płaszczyźnie przekroju poprzecznego suma prądów płynących po przewodach wynosi zero.

Poza prądem powierzchniowym w linii współosiowej występuje również prąd przesunięcia. Przypomnijmy, że wektor gęstości prądu przesunięcia to $\partial \vec{D} / \partial$ i dla rozpatrywanego przypadku (t = 0) opisuje go zależność ${\vec{i}}_{p} ω ε_{0} E_{0} (b / ρ) s i n (- β z) [A / m^{2}]$ . Prąd ten „płynie” między przewodami prowadnicy, linie tego prądu są tak skierowane jak linie pola elektrycznego, ale są przesunięte względem tego pola o ćwierć długości fali. W płaszczyźnie $z = λ / 2$ , gdzie pola elektryczne i magnetyczne osiągają wartości maksymalne, prąd przesunięcia jest równy zeru. Gęstość prądu przesunięcia wzdłuż osi z, jest maksymalna w płaszczyźnie $z = λ / 4$ i prąd płynie od przewodu wewnętrznego do zewnętrznego.

Omawiając falę płaską (moduł 2) wprowadziliśmy wektor Poyntinga. Zwrot wektora wskazuje kierunek przepływu mocy fali elektromagnetycznej, a wartość określa jej powierzchniową gęstość mocy. Dla fali płaskiej, w ustalonej chwili czasu i określonej płaszczyźnie prostopadłej do kierunku rozchodzenia się fali, wartość wektora Poyntinga jest stała.

Dla fali TEM w linii współosiowej wektor Poyntinga ma tylko składową równoległą do kierunku propagacji i zmienia się w czasie i wzdłuż osi z tak jak to miało miejsce dla fali płaskiej. Natomiast wartość wektora w przekroju poprzecznym maleje z kwadratem zmiennej $ρ$ .

Pole elektromagnetyczne w omawianej prowadnicy występuje w ograniczonej przestrzeni, między przewodami linii. Uśredniając w czasie wektor Poyntinga i obliczając jego całkę po przekroju poprzecznym otrzymujemy średnią w czasie moc fali w linii współosiowej. Ten sposób wyznaczania mocy przenoszonej przez falę elektromagnetyczną nazywamy „polowym” ponieważ do jej wyznaczenia potrzebne są natężenia pól elektrycznego i magnetycznego.

Przedstawione dotychczas wielkości związane z falą typu TEM w linii współosiowej (np. natężenia pól elektrycznego i magnetycznego, współczynnik propagacji, prędkości fazowa i grupowa, impedancja falowa) określamy mianem polowych, z racji ich wynikania z równań Maxwella.

Dla prowadnicy falowej definiujemy również parametry obwodowe (np. prąd, napięcie), które są pomocne między innymi w projektowaniu obwodów mikrofalowych zawierających tak odcinki linii transmisyjnej jak i elementy o stałych skupionych.

Stwierdziliśmy, że pole elektryczne fali typu TEM w przekroju poprzecznym prowadnicy jest potencjalne. Możemy wobec tego wyznaczyć jednoznacznie napięcie między przewodami linii współosiowej, które jest całką z wektora natężenia pola elektrycznego po krzywej leżącej w płaszczyźnie poprzecznej z = const o początku na przewodzie wewnętrznym i końcu znajdującym się na przewodzie zewnętrznym. Tak zdefiniowane napięcie nie zależy od drogi całkowania, ponieważ w/w pole jest potencjalne. Zauważmy, że dla linii współosiowej przyjęliśmy określone wartości potencjałów na przewodnikach i amplituda napięcia w linii jest równa różnicy tych potencjałów.

Jednoznacznie określone napięcie między przewodami jest cechą charakteryzująca wszystkie prowadnice TEM. Należy zaznaczyć, że w liniach transmisyjnych z falami typu nie-TEM pole elektryczne nie jest potencjalne, całka określająca napięcie na ogół zależy od drogi całkowania i wobec tego definiując napięcie należy określić tę drogę i zdawać sobie sprawę z niejednoznaczności tego parametru.

Na powierzchniach przewodów linii współosiowej występują prądy powierzchniowe, których gęstości są określone jednoznacznie warunkami brzegowymi. Prądy w obu przewodach linii, które są całkami z gęstości prądów, płyną tylko wzdłuż osi 0z, mają taką samą wartość i przeciwny zwrot.

Amplitudę prądu w linii, czyli np. na przewodzie wewnętrznym, wyznaczamy całkując gęstość prądu powierzchniowego, która zgodnie z warunkiem brzegowym równa jest co do wartości natężeniu pola magnetycznego, po obwodzie tego przewodu. Zależność opisująca amplitudę prądu w linii współosiowej proporcjonalna jest do amplitudy natężenia pola magnetycznego przy przewodzie wewnętrznym, która jest równa stosunkowi amplitudy natężenia pola elektrycznego i impedancji właściwej ośrodka. Prąd w linii współosiowej jest określony jednoznacznie. Własność to dotyczy wszystkich prowadnic TEM.

Zauważmy, że obliczając amplitudę napięcia w linii wybraliśmy taką płaszczyznę poprzeczną, w której pole elektryczne jest rzeczywiste. Amplituda prądu w tej płaszczyźnie będzie również rzeczywista dla linii wypełnionej dielektrykiem bezstratnym. Gdy ośrodek w linii współosiowej jest stratny to impedancja właściwa jest liczbą zespoloną i amplituda prądu również jest wielkością zespoloną.

Znając amplitudy napięcia i prądu w prowadnicy falowej można wyznaczyć „obwodowo” uśrednioną w czasie moc przenoszoną przez falę elektromagnetyczną posługując się zależnością P = (1/2)Re[UI*], gdzie I* to sprzężona amplituda prądu. Dla prowadnicy bezstratnej moc jest po prostu połową iloczynu amplitud napięcia i prądu. W związku z tym, że napięcie i prąd w linii TEM są zdefiniowane jednoznacznie to moce obliczone „polowo” oraz „obwodowo” są takie same. Łatwo sprawdzić, że tak jest dla linii współosiowej. Przy omawianiu falowodu prostokątnego zobaczymy, że w linii z falą nie-TEM moce wyznaczone polowo i obwodowo nie przyjmują takich samych wartości.

Rozważmy własności fali TEM w dwóch liniach współosiowych wypełnionych tym samym ośrodkiem, w których długość promienia przewodu zewnętrznego jest identyczna, a promień wewnętrzny jednej z nich jest kilkukrotnie większy niż drugiej. Jeżeli napięcie między przewodami tych linii będzie identyczne to wartości natężeń pól elektrycznego i magnetycznego w przekroju poprzecznym prowadnicy będą różne. Pozostałe własności fali TEM - takie jak współczynnik propagacji, prędkości fazowa i grupowa, impedancja falowa - będą identyczne. Badanie wielkości natężenia pola elektrycznego czy magnetycznego w celu rozróżnienia prowadnic falowych byłoby wysoce niepraktycznym sposobem.

Czy jest wygodny parametr charakteryzujący linię współosiową, który pozwoliłby rozróżnić podane wyżej prowadnice? Okazuje się, że takim parametrem jest impedancja charakterystyczna linii transmisyjnej.

Impedancja charakterystyczna prowadnicy falowej $(Z_{c})$ , w której rozchodzi się fala w jednym kierunku, może być zdefiniowana jedną z zależności:

Z_{c U I} = \frac{U}{I}

Z_{c P U} = \frac{U^{2}}{2 P}

Z_{c P I} = \frac{2 P}{I^{2}}

w których: U, I – amplitudy napięcia i prądu (w ogólności wielkości zespolone); P – średnia w czasie moc przenoszona przez falę elektromagnetyczną w linii (wielkość rzeczywista).

Przypomnijmy, że prowadnica falowa jest strukturą, której zadaniem jest przesyłanie fali z możliwie małymi stratami, więc w jej konstrukcji stosowane są dielektryki o małych stratach. Dla małostratnych linii transmisyjnych część urojona impedancji charakterystycznej jest na tyle mała, że często się ją zaniedbuje.

Dla prowadnicy TEM, ze względu na jednoznaczność prądu i napięcia w linii, wszystkie trzy wzory dają taką samą, jednoznacznie określoną wartość impedancji charakterystycznej.

Warto zapamiętać, że prowadnicę falową charakteryzują dwa parametry: współczynnik propagacji oraz impedancja charakterystyczna. Pierwszy z tych parametrów jest wielkością polową, której obliczenie wiąże się w ogólności z rozwiązaniem równań Maxwella. Drugi jest wielkością obwodową, wyznaczaną z zastosowaniem jednej z podanych definicji, przydatną przy analizie obwodów mikrofalowych.

Falowód prostokątny ma postać metalowej rury o przekroju prostokątnym. Przyjmijmy, że ścianki falowodu są doskonale przewodzące, a dielektryk wypełniający falowód jest liniowy, jednorodny, izotropowy i bezstratny. Pole elektromagnetyczne w falowodzie prostokątnym musi spełniać równania Maxwella, wynikające z nich równania Helmholtz’a oraz warunki brzegowe na granicy dielektryk – przewodnik. Przypomnijmy, że pola zależą sinusoidalnie od czasu i stosujemy zapis zespolony.

Falowód prostokątny jest prowadnicą falową, w której nie występują dwa niezależne przewody, a więc nie może rozchodzić się w nim fala elektromagnetyczna typu TEM. Do zbioru rodzajów pola elektromagnetycznego falowodu należą rodzaje typu E (TM) i H (TE). Dowolne pole elektromagnetyczne występujące w tym falowodzie można przedstawić jako superpozycję wymienionych rodzajów.

Rodzaje pola, które mogą rozchodzić się w falowodzie prostokątnym oznaczamy jako $E_{m n}$ i $H_{m n}$ . Liczby naturalne m i n nazywamy wskaźnikami albo indeksami rodzaju. Z warunków brzegowych wynika, że zmiany składowych wektorów pól elektrycznego i magnetycznego w płaszczyźnie xy opisują funkcje sinus lub cosinus. Przykładowo, dla rodzaju $E_{m n}$ składowa $E_{z}$ w płaszczyźnie xy (dla z = 0) jest proporcjonalna do wyrażenia $s i n (\frac{m π}{a} x) s i n (\frac{n π}{b} y)$ (składowa ta musi przyjmować wartość równą zeru na ściankach falowodu). Natomiast dla rodzaju Hmn składowa $H_{z}$ w płaszczyźnie z = 0 jest proporcjonalna do wyrażenia $s i n (\frac{m π}{a} x) s i n (\frac{n π}{b} y)$ (składowa ta osiąga maksimum na ściankach falowodu).

Wskaźnik m rodzaju pola oznacza więc liczbę zmian (liczbę połówek okresu funkcji sinus lub cosinus) pola wzdłuż dłuższego boku (a) falowodu, a wskaźnik n opisuje liczbę zmian pola wzdłuż któtszego boku (b) falowodu. Zmiany te dotyczą wszystkich składowych wektorów pól elektrycznego i magnetycznego występujących dla danego rodzaju pola.

Dla rodzajów typu E wskaźniki rodzaju nie mogą przyjmować wartości zerowych, bo w przeciwnym przypadku oznaczałoby to zerowanie się składowej $E_{z}$ a tym samym nie byłby to już rodzaj typu E.

Dla rodzajów typu H jeden i tylko jeden ze wskaźników rodzaju może być równy zeru. Oznacza to, że rozkład pola elektromagnetycznego takiego rodzaju jest stały wzdłuż jednej z osi w płaszczyźnie przekroju poprzecznego falowodu.

Dla danego rodzaju pola (o ustalonych wskaźnikach rodzaju) rozchodzącego się w kierunku +0z, zależność wszystkich występujących w nim składowych pól elektrycznego i magnetycznego wzdłuż kierunku propagacji jest opisana przez czynnik Parser nie mógł rozpoznać (błąd składni): {\displaystyle exp(–\gamma_z z)} , przy czym

γ_{z}

to współczynnik propagacji fali wzdłuż osi z. Współczynnik ten określa się w oparciu o równanie podane na slajdzie.

Rodzajowi o wskaźnikach m i n przyporządkowana jest pewna charakterystyczna wielkość wynikająca z wskaźników rodzaju i wymiarów falowodu, którą nazywamy granicznym współczynnik fazy $β_{g}$ . Podkreślić należy, że nie zależy ona od częstotliwości i dla falowodu prostokątnego jest taka sama dla rodzaju E jak i dla rodzaju H o danych wskaźnikach m, n.

Drugim składnikiem we wzorze na współczynnik propagacji jest współczynnik fazy fali płaskiej o częstotliwości f rozchodzącej się w dielektryku wypełniającym falowód. Wielkość ta rośnie liniowo z częstotliwością.

Z równania dyspersyjnego wynika, że dla rodzaju o wskaźnikach m, n w falowodzie o danych wymiarach a, b i wypełnionym bezstratnym dielektrykiem o przenikalności elektrycznej ε istnieje pewna charakterystyczna częstotliwość, dla której współczynnik propagacji $γ_{z}$ jest równy zeru. Częstotliwość tę nazywamy graniczną. Jest ona powiązana z granicznym współczynnikiem fazy oraz parametrami ośrodka wypełniającego falowód. Dany rodzaj pola elektromagnetycznego rozchodzi się w falowodzie dla częstotliwości większych od częstotliwości granicznej.

Wyobraźmy sobie, że podłączyliśmy falowód prostokątny do generatora sygnału i zwiększamy jego częstotliwość poczynając od zera. Rozchodzenie się fali w falowodzie zaobserwujemy wtedy, gdy częstotliwość będzie na tyle wysoka, że przekroczy wartość najniższej częstotliwości granicznej dla tego falowodu. Rodzaj pola o najniższej częstotliwości granicznej nazywamy rodzajem podstawowym i dla falowodu prostokątnego jest to rodzaj

H_{10}

.

W tabeli podano częstotliwości graniczne kilku pierwszych rodzajów w falowodzie wypełnionym powietrzem przeznaczonym do pracy w zakresie częstotliwości od 8.2 GHz do 12.4 GHz, który nazywamy pasmem X. W tym falowodzie rodzaj $H_{10}$ , i tylko ten rodzaj, może rozchodzić się od częstotliwości ok. 6.5 GHz. Poczynając od częstotliwości ok. 13.1 GHz w falowodzie mogą rozchodzić się dwa rodzaje, a od ok. 14.8 GHz trzy. Gdy w falowodzie występuje tylko jeden rodzaj to rozkład i parametry fali elektromagnetycznej są jednoznacznie określone, możemy je kontrolować i budować elementy funkcjonalne falowodowego toru mikrofalowego. Nie jest to możliwe przy występowaniu kilku rodzajów, które mają różne rozkłady pola i parametry (np. długość fali). Dlatego też pasmo pracy falowodu ogranicza się do częstotliwości, dla których w falowodzie występuje tylko rodzaj podstawowy.

W praktyce, zalecane pasmo pracy falowodu prostokątnego mieści się w zakresie od 1.2 do 1.9 razy częstotliwość graniczna rodzaju $H_{10}$ . Falowody wykonuje się z mosiądzu, aluminium, miedzi lub srebra. Są to materiały o wysokiej, ale skończonej konduktywności. Okazuje się, że tłumienie fali wynikające ze strat w przewodniku jest bardzo duże w pobliżu częstotliwości granicznej i maleje ze wzrostem częstotliwości. Dolna granica pasma pracy falowodu wynika z tłumienia fali w falowodzie, podczas gdy możliwość wzbudzenia wyższych rodzajów określa górną granicę pasma.

Falowody prostokątne wykorzystuje się w szeregu zastosowaniach – między innymi grzanie mikrofalowe, technika radarowa i satelitarna, radioastronomia, miernictwo mikrofalowe - obejmujących zakres częstotliwości od około jednego do kilkuset gigahertzów. Potrzebujemy znacznej liczby falowodów o wystandaryzowanych wymiarach, aby pokryć wymieniony zakres częstotliwości. Standardowe falowody w większości przypadków mają bok a dwukrotnie dłuższy od boku b, przy czym im wyższe są częstotliwości pracy falowodu tym mniejsze są jego wymiary. Przykładowo, wymiary falowodu prostokątnego na pasmo od 26.5 GHz do 40 GHz to a = 7.112 mm i b = 3.556 mm, a falowód o bokach 2.032 mm i 1.016 mm przeznaczony jest na zakres częstotliwości od 90 GHz do 140 GHz.

Wiemy już, że dla częstotliwości granicznej rodzaju o wskaźnikach m, n jego współczynnik propagacji jest równy zeru. Z równania dyspersyjnego falowodu wynikają zależności opisujące współczynnik propagacji poniżej i powyżej częstotliwości granicznej, które pokazano na slajdzie.

Gdy częstotliwość fali danego rodzaju jest mniejsza od jego częstotliwości granicznej to współczynnik propagacji jest wielkością rzeczywistą równą współczynnikowi tłumienia αz. Oznacza to, że amplitudy składowych wektorów pól elektrycznego i magnetycznego tego rodzaju zanikają wykładniczo, według Parser nie mógł rozpoznać (błąd składni): {\displaystyle exp(–\alpha_z z)} , bez zmiany fazy $(β_{z} = 0)$ . Tempo zanikania zależy od wartości współczynnika tłumienia i jest tym większe im znaczniejsza jest różnica między częstotliwością graniczną i częstotliwością fali.

Dla częstotliwości większych od $f_{g}$ współczynnik propagacji jest urojony i jego część urojona to współczynnik fazy $β_{z}$ . Fala elektromagnetyczna rozchodzi się wtedy w falowodzie bez zmiany amplitudy bo współczynnik tłumienia jest równy zeru. Współczynnik fazy dla każdego rodzaju pola w falowodzie nie jest liniową funkcją częstotliwości, a więc fala elektromagnetyczna w falowodzie wykazuje własności dyspersyjne. Dyspersja ta jest cechą propagacji fali w bezstratnym falowodzie, nie jest wywołana więc stratami czy właściwościami dyspersyjnymi ośrodka w falowodzie, i określamy ją mianem dyspersji rodzaju pola lub dyspersji modowej.

Z współczynnikiem fazy związane są takie parametry fali elektromagnetycznej jak długość fali oraz prędkości fazowa i grupowa. Te parametry określa się wtedy, gdy dany rodzaj pola rozchodzi się w falowodzie, czyli dla częstotliwości większych od jego częstotliwości granicznej.

Na wykresie przedstawione są charakterystyki częstotliwościowe współczynników tłumienia i fazy rodzaju podstawowego w wypełnionym powietrzem falowodzie prostokątnym na pasmo X. Przebiegi te wynikają z zależności zamieszczonych na poprzednim slajdzie. Dodatkowo, pokazano przebieg współczynnika fazy fali płaskiej w powietrzu w funkcji częstotliwości.

Dla każdego rodzaju pola elektromagnetycznego w falowodzie przebieg współczynników tłumienia i fazy jest analogiczny do charakterystyk zamieszczonych na wykresie.

Współczynnik tłumienia jest różny od zera dla częstotliwości mniejszych od częstotliwości granicznej rodzaju $H_{10}$ . Wraz z obniżaniem częstotliwości jego wartość rośnie i osiąga największą wartość $(2 π / c) f_{g} H_{10} = π / a$ dla częstotliwości równej zeru.

Współczynnik fazy monotonicznie rośnie z częstotliwością poczynając od częstotliwości granicznej. Nie jest to jednak wzrost liniowy. Gdy częstotliwość dąży do nieskończoności współczynnik fazy fali w falowodzie dąży asymptotycznie do współczynnika fazy fali płaskiej. Oznacza to, że dla częstotliwości znacznie większych od częstotliwości granicznej współczynnik fazy rodzaju pola w falowodzie zmienia się w przybliżeniu liniowo z częstotliwością. Charakterystyczną cechą fali dowolnego rodzaju rozchodzącej się w falowodzie jest to, że jej współczynnik fazy dla danej częstotliwości jest mniejszy od współczynnika fazy fali płaskiej dla tej częstotliwości. Innymi słowy, długość fali w falowodzie jest zawsze większa od długości fali płaskiej w materiale, którym wypełniono falowód.

Pamiętamy, że zerowy współczynnik propagacji występuje jedynie dla częstotliwości granicznej. Współczynnik fazy równy zeru oznacza, że długość fali jest nieskończenie wielka. Dodatkowo, zerowy jest również współczynnik tłumienia. W rezultacie, dla tej częstotliwości w każdej chwili czasu, rozkład pola elektromagnetycznego w falowodzie jest stały wzdłuż osi z.

Znając częstotliwościową zależność współczynnika fazy rodzaju pola w falowodzie możemy również określić przebiegi prędkości fazowej i grupowej. Na wykresie przedstawione są charakterystyki częstotliwościowe znormalizowanych (do prędkości fali płaskiej w powietrzu) prędkości fazowej i grupowej rodzaju podstawowego w wypełnionym powietrzem falowodzie prostokątnym na pasmo X.

Przebiegi tych prędkości dobrze ilustrują zjawisko dyspersji związane z propagacją fali elektromagnetycznej w bezstratnym falowodzie. Za miarę stopnia dyspersji można uznać tempo zmian prędkości w funkcji częstotliwości. Widzimy, że dyspersja jest tym większa im bliżej jesteśmy częstotliwości granicznej.

Dla każdego rodzaju pola w falowodzie iloczyn pędkości fazowej i grupowej jest stały i równy kwadratowi prędkości fali płaskiej w dielektryku, którym wypełniono falowód. Pamiętamy, że fala płaska rozchodzi się z prędkością światła w danym ośrodku.

Z wykresu prędkości fazowej widzimy, że jest ona zawsze większa od prędkości światła. Przypomnijmy, że jest to możliwe, ponieważ ta prędkość informuje jedynie o szybkości zmian argumentu funkcji trygonometrycznej, nie oznacza przesuwania się żadnego obiektu materialnego i nie dotyczą jej ograniczenia wynikające z szczególnej teorii względności. Natomiast przenoszenie energii fali elektromagnetycznej w falowodzie, które odbywa się z prędkością grupową, jest zawsze wolniejsze od prędkości światła.

Zajmijmy się teraz poznaniem rozkładu pola elektromagnetycznego w falowodzie prostokątnym dla rodzaju podstawowego.

Na slajdzie podano wyrażenia określające składowe zespolonych wektorów pól magnetycznego i elektrycznego dla fali rodzaju $H_{10}$ rozchodzącej się w kierunku +0z. Fala rozchodzi się, więc podane zależności opisują pola dla częstotliwości nie mniejszych od częstotliwości granicznej. Wektor natężenia pola magnetycznego ma składową wzdłużną $H_{z}$ , która jest wyróżnikiem fali typu H, oraz jedną składową poprzeczną $H_{x}$ . Pole elektryczne ma tylko składową $E_{y}$ .

Łatwo stwierdzić, patrząc na podane zależności, że pola elektryczne i magnetyczne spełniają warunki brzegowe na ściankach falowodu. Składowe $E_{y}$ i $H_{x}$ są równe zeru dla krańcach dłuższego boku falowodu, czyli na granicy dielektryk-metal pole elektryczne nie ma składowej stycznej, a składowa normalna znika dla pola magnetycznego. Z kolei składowa $H_{z}$ , która jest składową styczną, osiąga maksimum na tej granicy.

Dla rodzaju podstawowego w falowodzie prostokątnym drugi wskaźnik jest równy zeru i w konsekwencji składowe pola elektromagnetycznego nie zależą od zmiennej y oraz od długości krótszego boku falowodu.

Zauważmy, że amplitudy składowych poprzecznych $E_{y 0}$ i $H_{x 0}$ w różny sposób zmieniają się z częstotliwością, przy ustalonej wartości amplitudy składowej wzdłużnej $H_{z 0}$ . Współczynnik fazy $β_{z}$ jest równy zeru dla częstotliwości granicznej i wtedy znika składowa $H_{x}$ . Tak więc, dla tej częstotliwości rodzaj $H_{10}$ ma tylko dwie składowe $H_{z}$ i $E_{y}$ o stałych rozkładach wzdłuż osi z.

Składowe poprzeczne pól elektrycznego i magnetycznego w identyczny sposób zależą od zmiennych x i z. Definiujemy dla rodzaju H10 impedancję falową, analogicznie jak to czyniliśmy dla fali płaskiej czy fali typu TEM, jako stosunek wzajemnie prostopadłych i prostopadłych do kierunku propagacji składowych pól elektrycznego i magnetycznego. Impedancja ta jest proporcjonalna do impedancji właściwej ośrodka wypełniającego falowód i zmienia się odwrotnie proporcjonalnie do współczynnika fazy, a więc jej funkcyjna zależność od częstotliwości jest taka jak prędkości fazowej.

Podkreślić należy, że impedancję falową określamy dla każdego rodzaju pola elektromagnetycznego w falowodzie. Dla rodzaju typu H opisuje ją podana już zależność $Z_{f H} = Z β / β_{z}$ , a dla rodzaju typu E impedancja falowa to $Z_{f E} = Z β_{z} / β$ . Zauważmy, że w funkcji częstotliwości impedancje te dążą asymptotycznie do impedancji właściwej dielektryka w falowodzie.

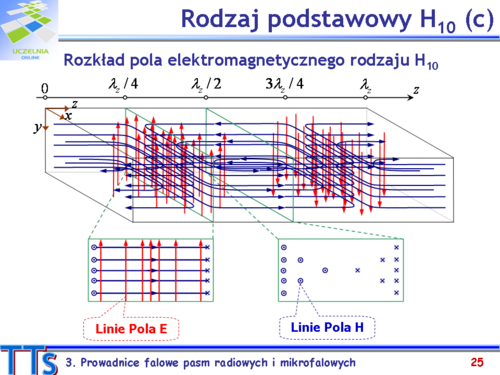
Wektory rzeczywiste natężeń pól magnetycznego i elektrycznego rodzaju

H_{10}

otrzymuje się mnożąc wektory zespolone przez

e x p (j ω t)

i wyznaczając części rzeczywiste tych nowo-powstałych wektorów. Przypomnijmy, że wyrażenie

ω t - β_{z} z

opisuje ruch fazy fali rozchodzącej się w kierunku +0z.

Składowa wzdłużna natężenia pola magnetycznego zmienia się wzdłuż osi z zgodnie z funkcją $c o s (ω t - β_{z} z)$ , a składowe poprzeczne $H_{x}$ i $E_{y}$ według funkcji $s i n (ω t - β_{z} z)$ . Wyróżnione składowe są przesunięte w fazie o $9 0^{\circ}$ . W danej chwili czasu płaszczyzna poprzeczna do kierunku rozchodzenia się fali, w której składowa $H_{z}$ jest maksymalna, odległa jest o ćwierć długości fali w falowodzie od płaszczyzny, w której maksymalne są składowe $H_{x}$ i $E_{y}$ . Można też zauważyć, że w płaszczyźnie z maksymalnymi składowymi poprzecznymi składowa wzdłużna jest równa zeru i vice versa.

Znając wyrażenia opisujące pole elektromagnetyczne fali rodzaju podstawowego w falowodzie prostokątnym można obliczyć wektor Poyntinga i określić polowo moc przepływającą przez falowód. Zauważmy, że na wartość wektora Poyntinga, a tym samym na wielkość mocy fali, wpływają jedynie składowe poprzeczne wektorów pól elektrycznego i magnetycznego, i dla rodzaju $H_{10}$ są to $E_{y}$ i $H_{x}$ .

Pytania sprawdzające

(jeśli potrafisz na nie odpowiedzieć, to znaczy, że opanowałeś/aś materiał wykładu)

Wymień i scharakteryzuj najważniejsze parametry prowadnicy falowej.
Przypomnij sobie jakie mody mogą rozchodzić się w falowodach i scharakteryzuj je.
Co to jest dyspersja, w jakich warunkach i dlaczego dyspersja utrudnia transmisję sygnału.
Przeanalizuj przyczyny powstawania strat przy transmisji mocy prowadnicami falowymi.
Na czym polega efekt naskórkowości?
Opisz kolejno prowadnice typu TEM.
Narysuj konfigurację pól E i H dla modu podstawowego i naszkicuj kierunki przepływu prądów w ściankach falowodu prostokątnego.
Dlaczego nie stosujemy falowodów prostokątnych, dla których stosunek a/b=1?
W jakim pasmie częstotliwości może pracować falowód prostokątny?
W jakim pasmie może pracować falowód cylindryczny?
Jak uzasadnisz fakt, że obwodem zastępczym odcinka falowodu prostokątnego jest odcinek linii dwuprzewodowej?
Jak zbudowana jest i jakie ma właściwości prowadnica mikropaskowa?
Jak zbudowana jest i jakie ma właściwości linia koplanarna?
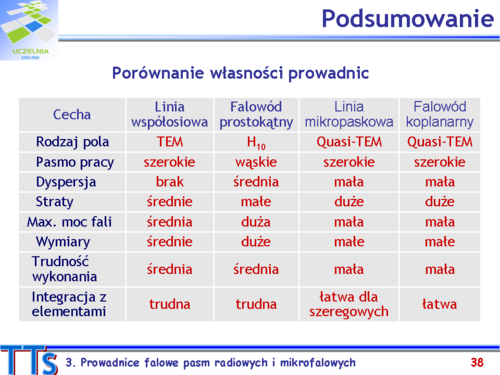
Jakie są obszary zastosowań linii współosiowej, linii mikropaskowej i falowodu prostokątnego? Aby to uzasadnić porównaj parametry wymienionych typów prowadnic.
Wymień argumenty przemawiające za rozwojem technologii i konstrukcji Mikrofalowych Monolitycznych Układów Scalonych na krzemie i arsenku galu.

Słownik

Częstotliwość graniczna - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.

Zestawienie typów fal:

Fala typu TEM - wektory pola E i H leżą w płaszczyźnie prostopadłej do kierunku propagacji.
Fala typu TE (zwana też H) - pole E posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole H posiada składowe w kierunku propagacji fali.
Fala typu TM (zwana też E) - pole H posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole E posiada składowe w kierunku propagacji fali.
Fala typu EH - zarówno pole E jak i pole H tej fali posiadają składowe w kierunku propagacji.

Linie TEM:

Linia współosiowa.
Linia dwuprzewodowa.
Symetryczna linia paskowa.

Linie Quasi-TEM:

Niesymetryczna linia paskowa:
Linia koplanarna (falowód koplanarny).
Linia koplanarna paskowa.

Linie falowodowe:

Falowód prostokątny. Mod podstawowy typu TE10 (H10).
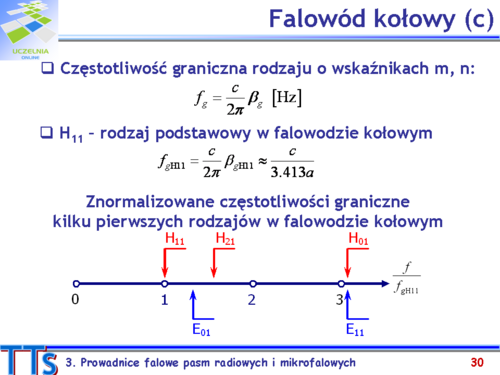
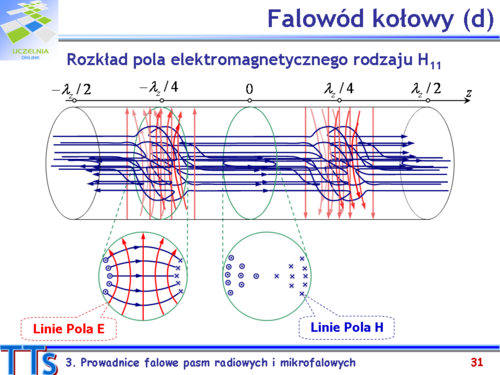
Falowód kołowy (cylindryczny). Mod podstawowy typu TE11 (H11).

Mod (rodzaj) podstawowy dla danego falowodu - to mod fali o najmniejszej

Bibliografia

Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2.</math>

@@ Linia 412: / Linia 412: @@
 {| border="0" cellpadding="4" width="100%"
 |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd24.png|thumb|500px]]
-|valign="top"|
+|valign="top"|Wektory rzeczywiste natężeń pól magnetycznego i elektrycznego rodzaju <math>H_{10}\,</math> otrzymuje się mnożąc wektory zespolone przez <math>exp(j\omega t)</math> i wyznaczając części rzeczywiste tych nowo-powstałych wektorów. Przypomnijmy, że wyrażenie <math>\omega t - \beta_z z</math> opisuje ruch fazy fali rozchodzącej się w kierunku +0z.
+Składowa wzdłużna natężenia pola magnetycznego zmienia się wzdłuż osi z zgodnie z funkcją <math>cos(\omega t - \beta_z z)</math>, a składowe poprzeczne <math>H_x\,</math> i <math>E_y\,</math> według funkcji <math>sin(\omega t - \beta_z z)</math>. Wyróżnione składowe są przesunięte w fazie o <math>90^\circ\,</math>. W danej chwili czasu płaszczyzna poprzeczna do kierunku rozchodzenia się fali, w której składowa <math>H_z\,</math> jest maksymalna, odległa jest o ćwierć długości fali w falowodzie od płaszczyzny, w której maksymalne są składowe <math>H_x\,</math> i <math>E_y\,</math>. Można też zauważyć, że w płaszczyźnie z maksymalnymi składowymi poprzecznymi składowa wzdłużna jest równa zeru i vice versa.
+Znając wyrażenia opisujące pole elektromagnetyczne fali rodzaju podstawowego w falowodzie prostokątnym można obliczyć wektor Poyntinga i określić polowo moc przepływającą przez falowód. Zauważmy, że na wartość wektora Poyntinga, a tym samym na wielkość mocy fali, wpływają jedynie składowe poprzeczne wektorów pól elektrycznego i magnetycznego, i dla rodzaju <math>H_{10}\,</math> są to <math>E_y\,</math> i <math>H_x\,</math>.
 |}

TTS Moduł 3: Różnice pomiędzy wersjami

Wersja z 13:59, 16 sty 2007

Spis treści

Wykład

Pytania sprawdzające

Słownik

Bibliografia

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia