PEE Moduł 14: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\displaystyle ” na „” |
||
| Linia 30: | Linia 30: | ||
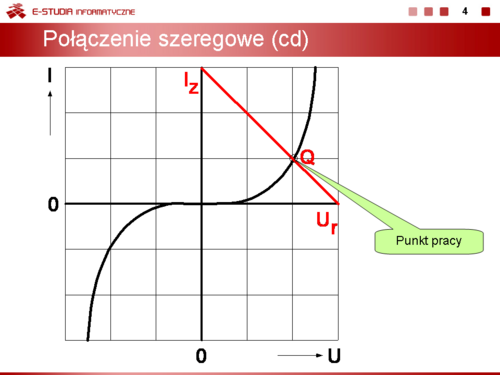
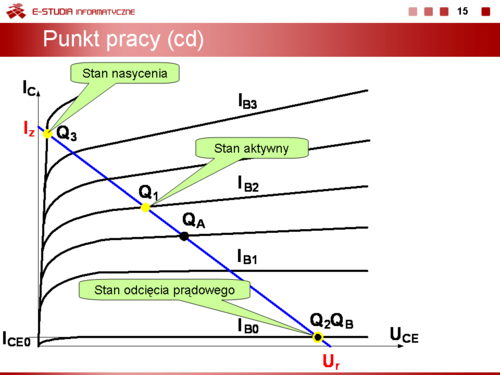
|valign="top"|W układzie współrzędnych kartezjańskich I = f(U) rysujemy charakterystykę prądowo-napięciową elementu nieliniowego oraz charakterystykę części liniowej obwodu. Ponieważ charakterystyki elementów części liniowej są liniami prostymi to także wypadkowa charakterystyka prądowo-napięciowa tej części obwodu jest także prostą. Aby ją narysować wystarczy wyznaczyć dwa punkty tej charakterystyki. Pierwszy przy zwarciu, a drugi przy rozwarciu zacisków A i B obwodu przedstawionego na slajdzie 3. Odpowiadające tym stanom punkty mają współrzędne | |valign="top"|W układzie współrzędnych kartezjańskich I = f(U) rysujemy charakterystykę prądowo-napięciową elementu nieliniowego oraz charakterystykę części liniowej obwodu. Ponieważ charakterystyki elementów części liniowej są liniami prostymi to także wypadkowa charakterystyka prądowo-napięciowa tej części obwodu jest także prostą. Aby ją narysować wystarczy wyznaczyć dwa punkty tej charakterystyki. Pierwszy przy zwarciu, a drugi przy rozwarciu zacisków A i B obwodu przedstawionego na slajdzie 3. Odpowiadające tym stanom punkty mają współrzędne | ||
<math> | <math>I_z=\frac{E}{R},\, U_z = 0 V</math> przy zwarciu, | ||
<math> | <math>I_r = 0\, A,\, U_r = E</math> przy rozwarciu. | ||
Punkt przecięcia prostej z charakterystyką elementu nieliniowego wyznacza punkt pracy Q tego elementu oraz obwodu liniowego. Często prostą, która jest obrazem charakterystyki części liniowej obwodu nazywamy prostą obciążenia elementu nieliniowego (np. diody lub tranzystora). | Punkt przecięcia prostej z charakterystyką elementu nieliniowego wyznacza punkt pracy Q tego elementu oraz obwodu liniowego. Często prostą, która jest obrazem charakterystyki części liniowej obwodu nazywamy prostą obciążenia elementu nieliniowego (np. diody lub tranzystora). | ||
| Linia 43: | Linia 43: | ||
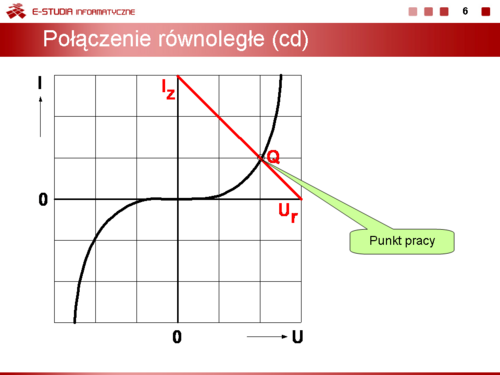
|valign="top"|Przy połączeniu równoległym suma prądów jest stała i równa I. | |valign="top"|Przy połączeniu równoległym suma prądów jest stała i równa I. | ||
<math> | <math>I=\frac{U_Q}{R}+I_Q</math> | ||
Podobnie jak przy połączeniu szeregowym prąd IQ oraz napięcie UQ określają współrzędne punktu pracy elementu nieliniowego. | Podobnie jak przy połączeniu szeregowym prąd IQ oraz napięcie UQ określają współrzędne punktu pracy elementu nieliniowego. | ||
| Linia 55: | Linia 55: | ||
i rozwierając zaciski A i B obwodu otrzymujemy współrzędne prostej obciążenia | i rozwierając zaciski A i B obwodu otrzymujemy współrzędne prostej obciążenia | ||
<math> | <math>I_z = I,\, U_z = 0\, V</math> przy zwarciu, | ||
<math>I_r = 0\, A,\, U_r = I\cdot R</math> przy rozwarciu. | <math>I_r = 0\, A,\, U_r = I\cdot R</math> przy rozwarciu. | ||
Punkt przecięcia prostej obciążenia z charakterystyką elementu nieliniowego wyznacza punkt pracy Q tego elementu oraz punkt pracy części liniowej obwodu. | Punkt przecięcia prostej obciążenia z charakterystyką elementu nieliniowego wyznacza punkt pracy Q tego elementu oraz punkt pracy części liniowej obwodu. | ||
| Linia 75: | Linia 75: | ||
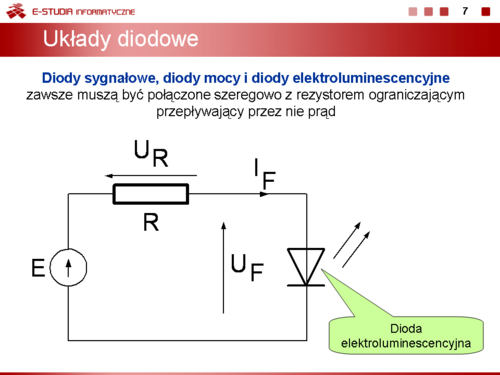
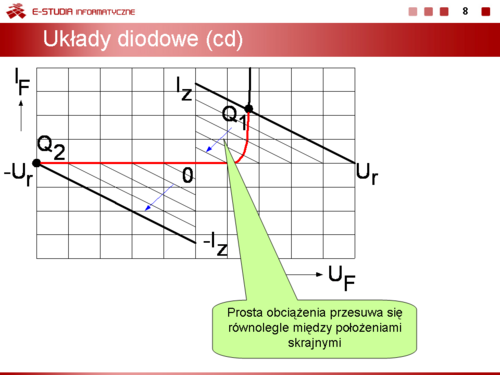
|valign="top"|Na slajdzie 8 przedstawiono zmianę położenia prostej obciążenia przy zasilaniu układu rezystor-dioda ze źródła napięcia przemiennego: | |valign="top"|Na slajdzie 8 przedstawiono zmianę położenia prostej obciążenia przy zasilaniu układu rezystor-dioda ze źródła napięcia przemiennego: | ||
<math> | <math>u(\omega t)=\sqrt{2}\cdot U\cdot sin\omega t</math> | ||
Przy takim sterowaniu dioda pracuje w dwóch stanach: stanie przewodzenia i stanie zaporowy. Punkt pracy przesuwa się po charakterystyce prądowo-napięciowej pomiędzy dwoma skrajnymi położeniami <math>Q_1\,</math> i <math>Q_2\,</math> | Przy takim sterowaniu dioda pracuje w dwóch stanach: stanie przewodzenia i stanie zaporowy. Punkt pracy przesuwa się po charakterystyce prądowo-napięciowej pomiędzy dwoma skrajnymi położeniami <math>Q_1\,</math> i <math>Q_2\,</math> | ||
| Linia 129: | Linia 129: | ||
Przy zwarciu można napisać | Przy zwarciu można napisać | ||
<math> | <math>E_C-I_C_z\cdot R_C+I_E_z\cdot R_E</math> gdzie <math>I_C_z = \alpha_0\cdot I_E_z\,</math> | ||
Zatem | Zatem | ||
<math> | <math>I_z=I_C_z=\frac{E_C}{R_C+\frac{R_E}{\alpha_0}}U_z = U_C_E_z = 0\, V</math> | ||
Przy rozwarciu | Przy rozwarciu | ||
| Linia 175: | Linia 175: | ||
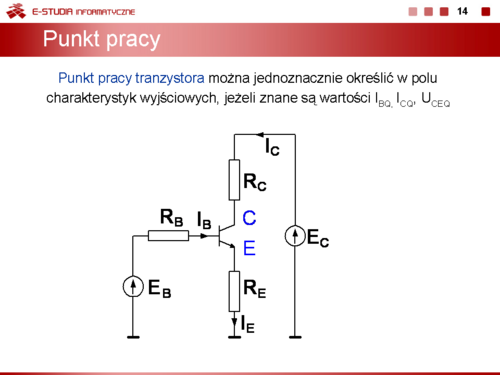
Obwód przedstawiony na slajdzie 18 można opisać układem równań | Obwód przedstawiony na slajdzie 18 można opisać układem równań | ||
<math> | <math>E_B=I_{BQ}\cdot R_B+I_{EQ}\cdot R_E+U_{BEQ}</math> | ||
<math> | <math>E_C=I_{CQ}\cdot R_C+I_{EQ}\cdot R_E+U_{CEQ}</math> | ||
<math> | <math>I_{EQ}=I_{CQ}+I_{BQ}</math> | ||
<math> | <math>I_{CQ}=\beta_{0Q}\cdot I_{BQ}+(1+\beta _{0Q})\cdot I_{CB0Q}</math> | ||
Przekształcając ten układ obliczamy współrzędne punktu pracy | Przekształcając ten układ obliczamy współrzędne punktu pracy | ||
<math> | <math>I_{CQ}=\frac{\beta_{0Q}(E_B-U_{BEQ})+(\beta_{0Q}+1)I_{CB0Q}(R_B+R_E)}{R_B+(1+\beta_{0Q})R_E}</math> | ||
<math> | <math>U_{CEQ}=E_C-I_{CQ}\bigg[R_C+\frac{(\beta_{0Q}+1)R_E}{\beta_{0Q}}\bigg]+\frac{\beta _{0Q}+1}{\beta_{0Q}}I_{CB0Q}R_E</math> | ||
|} | |} | ||
| Linia 197: | Linia 197: | ||
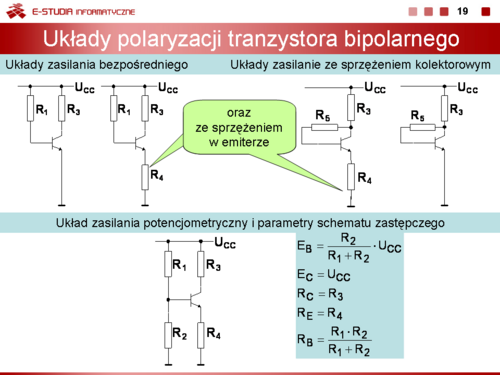
Np. Zastępcze parametry obwodu zasilania dla układu z potencjometrycznym zasilaniem bazy i sprzężeniem w emiterze są odpowiednio równe: | Np. Zastępcze parametry obwodu zasilania dla układu z potencjometrycznym zasilaniem bazy i sprzężeniem w emiterze są odpowiednio równe: | ||
<math> | <math>E_B\frac{R_2}{R_1+R_2}\cdot U_{CC}</math> | ||
<math> | <math>E_C=U_{CC}</math> | ||
<math> | <math>R_C=R_3</math> | ||
<math> | <math>R_E=R_4</math> | ||
<math> | <math>R_B=\frac{R_1\cdot R_2}{R_1+R_2}</math> | ||
|} | |} | ||
| Linia 217: | Linia 217: | ||
Przyjmując, że zmianie ulegają parametry tranzystora równanie stabilizacji punktu pracy ma następującą postać | Przyjmując, że zmianie ulegają parametry tranzystora równanie stabilizacji punktu pracy ma następującą postać | ||
<math> | <math>dI_{CQ}=\frac{\delta I_{CQ}}{\delta I_{CB0}}dI_{CB0}+\frac{\delta I_{CQ}}{\delta U_{BE}}dU_{BE}+\frac{\delta I_{CQ}}{\delta \beta_0}d\beta_0</math> | ||
| Linia 227: | Linia 227: | ||
|valign="top"|Poszczególne pochodne cząstkowe nazywamy współczynnikami stabilizacji | |valign="top"|Poszczególne pochodne cząstkowe nazywamy współczynnikami stabilizacji | ||
<math> | <math>S_i=\frac{dI_{CQ}}{dI_{CB0}}\bigg|_{\begin{matrix} U_{BE}=const \\ \beta_0=const \end{matrix}}</math> | ||
<math> | <math>S_u=\frac{dI_{CQ}}{dU_{BE}}\bigg|_{\begin{matrix} I_{CB0}=const \\ \beta_0=const \end{matrix}}</math> | ||
<math> | <math>S_{\beta}=\frac{dI_{CQ}}{d\beta_0}\bigg|_{\begin{matrix} U_{BE}=const \\ I_{CB0}=const \end{matrix}}</math> | ||
Zagadnienia związane ze stabilizacją termiczną punktu pracy dotyczą wyłącznie składowych stałych prądów i napięć polaryzujących tranzystor bipolarny. A zatem na wartość współczynników stabilizacji nie wpływają wartości parametrów małosygnałowych (dynamicznych). Dla tranzystorów krzemowych istotniejszy jest współczynnik <math>S_u\,</math> a nie <math>S_i\,</math>. | Zagadnienia związane ze stabilizacją termiczną punktu pracy dotyczą wyłącznie składowych stałych prądów i napięć polaryzujących tranzystor bipolarny. A zatem na wartość współczynników stabilizacji nie wpływają wartości parametrów małosygnałowych (dynamicznych). Dla tranzystorów krzemowych istotniejszy jest współczynnik <math>S_u\,</math> a nie <math>S_i\,</math>. | ||
| Linia 250: | Linia 250: | ||
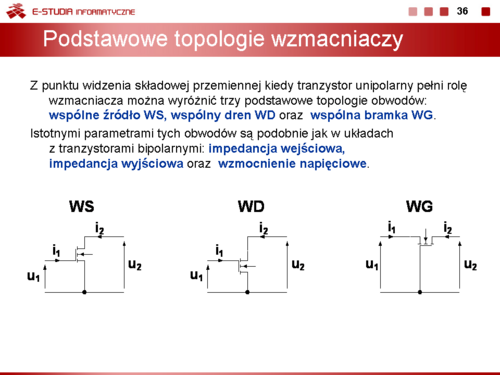
|valign="top"|Istotnymi parametrami tych obwodów są | |valign="top"|Istotnymi parametrami tych obwodów są | ||
<math> | <math>r_{WE}=\frac{u_1}{i_1}\bigg|_{i_2=0}</math> impedancja wejściowa, | ||
<math> | <math>r_{WY}=\frac{u_2}{i_2}\bigg|_{u_1=0}</math> impedancja wyjściowa, | ||
<math> | <math>k_{U}=\frac{u_2}{u_1}\bigg|_{i_2=0}</math> wzmocnienie napięciowe. | ||
Znak minus w definicji rezystancji wyjściowej wynika z przyjęcia, przeciwnego niż to jest przyjęte w teorii czwórników, zwrotu prądu <math>i_2\,</math> | Znak minus w definicji rezystancji wyjściowej wynika z przyjęcia, przeciwnego niż to jest przyjęte w teorii czwórników, zwrotu prądu <math>i_2\,</math> | ||
| Linia 266: | Linia 266: | ||
|valign="top"|Przy wyznaczaniu tych parametrów stosuje się małosygnałowy model tranzystora bipolarnego opisany równaniami macierzy hybrydowej <math>h\,</math> z parametrami w postaci uniwersalnej. | |valign="top"|Przy wyznaczaniu tych parametrów stosuje się małosygnałowy model tranzystora bipolarnego opisany równaniami macierzy hybrydowej <math>h\,</math> z parametrami w postaci uniwersalnej. | ||
<math> | <math>u_{BE}=i_B\cdot r_{BE}+u_{CE}\cdot k_f</math> | ||
<math> | <math>i_C=i_B\cdot \beta +u_{CE}\cdot \frac{1}{r_{CE}}</math> | ||
|} | |} | ||
| Linia 276: | Linia 276: | ||
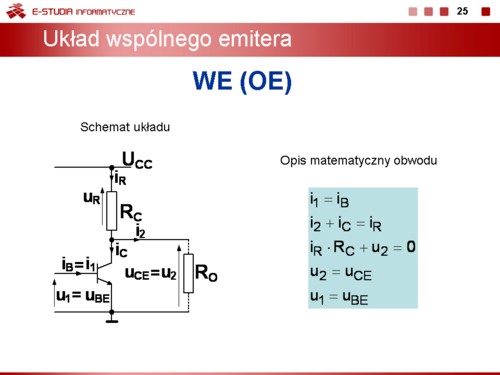
|valign="top"|Dla układu wspólnego emitera WE można zapisać | |valign="top"|Dla układu wspólnego emitera WE można zapisać | ||
<math> | <math>i_1=i_B</math> | ||
<math> | <math>i_2+i_C=i_R</math> | ||
<math> | <math>i_R\cdot R_C+u_2=0</math> | ||
<math> | <math>u_2=u_{CE}</math> | ||
<math> | <math>u_1=u_{BE}</math> | ||
Warunek <math> | Warunek <math>i_R\cdot R_C + u_2 = 0</math> oznacza, że przyrosty napięć na rezystorze kolektorowym | ||
i tranzystorze kompensują się. Wynika to z faktu, że napięcie zasilania <math>U_{CC}\,</math> jest stałe tzn. nie zmienia się w czasie | i tranzystorze kompensują się. Wynika to z faktu, że napięcie zasilania <math>U_{CC}\,</math> jest stałe tzn. nie zmienia się w czasie | ||
|} | |} | ||
| Linia 293: | Linia 293: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd26.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd26.png|thumb|500px]] | ||
|valign="top"|Przy obliczaniu wzmocnienia napięciowego i rezystancji wejściowej zakładamy, że wzmacniacz jest nieobciążony co oznacza, że <math> | |valign="top"|Przy obliczaniu wzmocnienia napięciowego i rezystancji wejściowej zakładamy, że wzmacniacz jest nieobciążony co oznacza, że <math>i_2 = 0</math>, a zatem <math>i_C = i_R</math> oraz <math>i_C=-\frac {u_2}{R_C}</math> | ||
Można zatem napisać | Można zatem napisać | ||
<math> | <math>u_1=i_1\cdot r_{BE}+u_2\cdot k_f</math> | ||
<math> | <math>-\frac{u_2}{R_C}=i_1\cdot \beta +u_2\cdot \frac{1}{r_{CE}}</math> | ||
Rugując z tego układu równań prąd <math>i_1\,</math> wzmocnienie napięciowe jest opisane zależnością | Rugując z tego układu równań prąd <math>i_1\,</math> wzmocnienie napięciowe jest opisane zależnością | ||
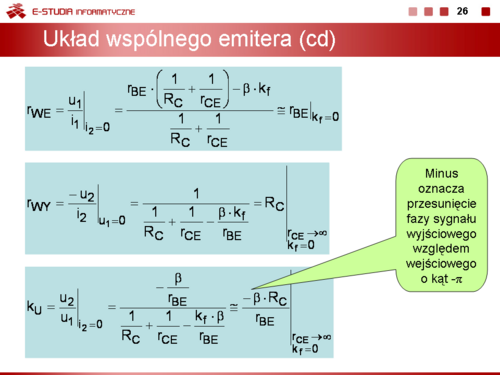
<math> | <math>k_U=\frac{u_2}{u_1}\bigg|_{i_2=0} =\frac{-\frac{\beta}{r_{BE}}}{\frac{1}{R_C}+\frac{1}{r_{CE}}-\frac{k_f\cdot \beta}{r_{BE}}}\cong \frac{-\beta\cdot R_C}{r_{BE}}\bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}</math> | ||
Znak minus we wzorze oznacza, że układ odwraca fazę sygnału (przesuwa sygnał wyjściowy w fazie względem sygnału wejściowego o kąt <math>\pi</math>. | Znak minus we wzorze oznacza, że układ odwraca fazę sygnału (przesuwa sygnał wyjściowy w fazie względem sygnału wejściowego o kąt <math>\pi</math>. | ||
Rugując z układu równań napięcie <math>u_2</math> rezystancja wejściowej jest dana wzorem | Rugując z układu równań napięcie <math>u_2</math> rezystancja wejściowej jest dana wzorem | ||
<math> | <math>r_{WE}=\frac{u_1}{i_1}\bigg|_{i_2=0} =\frac{r_{BE}\cdot \left(\frac{1}{R_C}+\frac{1}{r_{CE}}\right)-\beta\cdot k_f}{\frac{1}{R_C}+\frac{1}{r_{CE}}}\cong r_{BE}\bigg|_{k_f=0}</math> | ||
Przy obliczaniu rezystancji wyjściowej należy wzmacniacz obciążyć, a zatem | Przy obliczaniu rezystancji wyjściowej należy wzmacniacz obciążyć, a zatem | ||
<math> | <math>i_C=i_R-i_2=-\frac{u_2}{R_C}-i_2</math> | ||
Można zatem napisać | Można zatem napisać | ||
<math> | <math>0=i_1\cdot r_{BE}+u_2\cdot k_f</math> | ||
<math> | <math>-\frac{u_2}{R_C}-i_2=i_1\cdot \beta +u_2\cdot \frac{1}{r_{CE}}</math> | ||
Rugując z tego układu równań napięcie <math>u_2\,</math> rezystancja wyjściowa jest opisane zależnością | Rugując z tego układu równań napięcie <math>u_2\,</math> rezystancja wyjściowa jest opisane zależnością | ||
<math> | <math>r_{WY}=\frac{-u_2}{i_2}\bigg|_{u_1=0} =\frac{1}{\frac{1}{R_C}+\frac{1}{r_{CE}}-\frac{\beta\cdot k_f}{r_{BE}}}= R_C \bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}</math> | ||
Podobnie jak dla układu WE postępujemy przy wyznaczaniu podstawowych parametrów wzmacniacza w układach wspólnego kolektora i wspólnej bazy | Podobnie jak dla układu WE postępujemy przy wyznaczaniu podstawowych parametrów wzmacniacza w układach wspólnego kolektora i wspólnej bazy | ||
| Linia 333: | Linia 333: | ||
|valign="top"|Dla układu wspólnego kolektora WK, często nazywanego także wtórnikiem emiterowym można zapisać | |valign="top"|Dla układu wspólnego kolektora WK, często nazywanego także wtórnikiem emiterowym można zapisać | ||
<math> | <math>i_1=i_B</math> | ||
<math> | <math>u_1=u_{BE}+u_2</math> | ||
<math> | <math>u_2+u_{CE}=0</math> | ||
<math> | <math>i_E=i_1+i_C=i_R+i_2</math> | ||
<math> | <math>i_R=\frac{u_2}{R_E}</math> | ||
|} | |} | ||
| Linia 351: | Linia 351: | ||
|valign="top"|Wzmocnienie napięciowe tego układu jest bliskie, ale zawsze mniejsze od jedności | |valign="top"|Wzmocnienie napięciowe tego układu jest bliskie, ale zawsze mniejsze od jedności | ||
<math> | <math>k_U=\frac{u_2}{i_1}\bigg|_{i_2=0} =\frac{1}{1+\frac{R_{BE}}{\beta +1}\left(\frac{1}{R_E}+\frac{1}{r_{CE}}\right)-k_f}\cong\frac{1}{1+\frac{r_{BE}}{\beta +1}}\bigg|_{\begin{matrix} r_{CE}\to\infty \\ k_f=0\end{matrix}}\approx 1\frac{V}{V}</math> | ||
Rezystancja wejściowa jest równa | Rezystancja wejściowa jest równa | ||
<math> | <math>r_{WE}=\frac{u_1}{i_1}\bigg|_{i_2=0}= r_{BE}+\frac{(1-k_f)\cdot (1+\beta)}{\frac{1}{R_E}+\frac{1}{r_{CE}}}\cong r_{BE}+(1+\beta)\cdot R_E\bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}\approx\beta\cdot R_E</math> | ||
a rezystancja wyjściowa | a rezystancja wyjściowa | ||
<math> | <math>r_{WY}=\frac{-u_2}{i_2}\bigg|_{u_1=0}=\frac{1}{\frac{1}{R_E}+\frac{1}{r_{CE}}+\frac{(1-k_f)\cdot (1+\beta)}{r_{BE}}}\cong \frac{1}{\frac{1}{R_E}+\frac{1+\beta}{r_{BE}}}\bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}\approx\frac{r_{BE}}{\beta}</math> | ||
|} | |} | ||
| Linia 367: | Linia 367: | ||
|valign="top"|Dla układu wspólnej bazy WB można zapisać: | |valign="top"|Dla układu wspólnej bazy WB można zapisać: | ||
<math> | <math>i_1=-i_E</math> | ||
<math> | <math>u_1=-u_{BE}</math> | ||
<math> | <math>u_2-u_1=u_{CE}</math> | ||
<math> | <math>i_R=i_C+i_2</math> | ||
<math> | <math>i_R\cdot R_C+u_2=0</math> | ||
<math> | <math>i_E=i_C+i_B</math> | ||
|} | |} | ||
| Linia 387: | Linia 387: | ||
*wzmocnienie napięciowe | *wzmocnienie napięciowe | ||
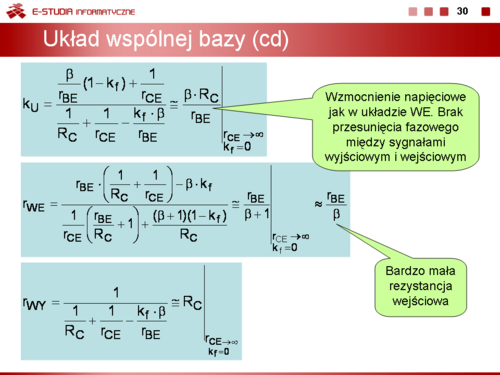
<math> | <math>k_U=\frac{\displaystyle\frac{\beta}{r_{BE}}(1-k_f)+\frac{1}{r_{CE}}}{\frac{1}{R_C}+\frac{1}{r_{CE}}-\frac{\beta\cdot k_f}{r_{BE}}}\cong \frac{\beta\cdot R_C}{r_{BE}} \bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}</math> | ||
*rezystancja wejściowa | *rezystancja wejściowa | ||
<math> | <math>r_{WE}=\frac{u_1}{i_1}\bigg|_{i_2=0} =\frac{r_{BE}\cdot \left(\frac{1}{R_C}+\frac{1}{r_{CE}}\right)-\beta\cdot k_f}{\frac{1}{r_{CE}}\left(\frac{r_{BE}}{R_C}+1\right)+\frac{(\beta+1)\cdot (1-k_f)}{r_{BE}}}}\cong \frac{r_{BE}}{\beta +1}\bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}</math> | ||
*rezystancja wyjściowa | *rezystancja wyjściowa | ||
<math> | <math>r_{WY} =\frac{1}{\frac{1}{R_C}+\frac{1}{r_{CE}}-\frac{k_f \cdot \beta }{r_{BE}}}\cong R_C \bigg|_{\begin{matrix} r_{CE}\to \infty \\ k_f=0 \end{matrix}}</math> | ||
|} | |} | ||
| Linia 413: | Linia 413: | ||
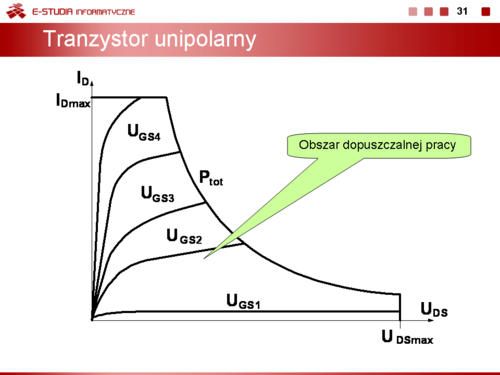
Punkt pracy tranzystora można jednoznacznie określić w polu charakterystyk wyjściowych, jeżeli znane są <math>U_{GSQ},\, I_{DQ},\, U_{DSQ}\,</math>. Załóżmy, że dane są charakterystyki wyjściowe tranzystora pracującego w układzie wzmacniacza przedstawionego na slajdzie 32. Postępując podobnie jak w układach z tranzystorami bipolarnymi możemy oddzielić część liniową obwodu od części nieliniowej. Część nieliniowa (tranzystor) ma znaną charakterystykę prądowo-napięciową. Charakterystyka części liniowej obwodu jest liniowa. Dwa punktu tej charakterystyki określamy zwierając i rozwierając elektrody D i S tranzystora. | Punkt pracy tranzystora można jednoznacznie określić w polu charakterystyk wyjściowych, jeżeli znane są <math>U_{GSQ},\, I_{DQ},\, U_{DSQ}\,</math>. Załóżmy, że dane są charakterystyki wyjściowe tranzystora pracującego w układzie wzmacniacza przedstawionego na slajdzie 32. Postępując podobnie jak w układach z tranzystorami bipolarnymi możemy oddzielić część liniową obwodu od części nieliniowej. Część nieliniowa (tranzystor) ma znaną charakterystykę prądowo-napięciową. Charakterystyka części liniowej obwodu jest liniowa. Dwa punktu tej charakterystyki określamy zwierając i rozwierając elektrody D i S tranzystora. | ||
Ponieważ <math> | Ponieważ <math>E_D=I_{Dz}\cdot (R_D+R_S)</math> | ||
Zatem przy zwarciu D i S można napisać | Zatem przy zwarciu D i S można napisać | ||
<math> | <math>I_z=I_{Dz}=\frac{E_D}{R_D+R_S}</math> | ||
<math> | <math>U_z=U_{DSz}=0\, V</math> | ||
Przy rozwarciu | Przy rozwarciu | ||
<math> | <math>I_r=0\,A,\, U_r=E_D</math> | ||
Punkt przecięcia tak wyznaczonej prostej (tzw. prostej obciążenia) z charakterystyką tranzystora odpowiadającą napięciu <math>U_{GS}\,</math>, które w tym wypadku będzie również równe napięciu <math>U_{GSQ}\,</math> wyznaczy współrzędne punktu pracy </math>I_{DQ}\,</math> oraz <math>U_{DSQ}\,</math> wyznaczy współrzędne punktu pracy <math>I_{DQ}\,</math> oraz <math>U_{DSQ}\,</math>. | Punkt przecięcia tak wyznaczonej prostej (tzw. prostej obciążenia) z charakterystyką tranzystora odpowiadającą napięciu <math>U_{GS}\,</math>, które w tym wypadku będzie również równe napięciu <math>U_{GSQ}\,</math> wyznaczy współrzędne punktu pracy </math>I_{DQ}\,</math> oraz <math>U_{DSQ}\,</math> wyznaczy współrzędne punktu pracy <math>I_{DQ}\,</math> oraz <math>U_{DSQ}\,</math>. | ||
| Linia 466: | Linia 466: | ||
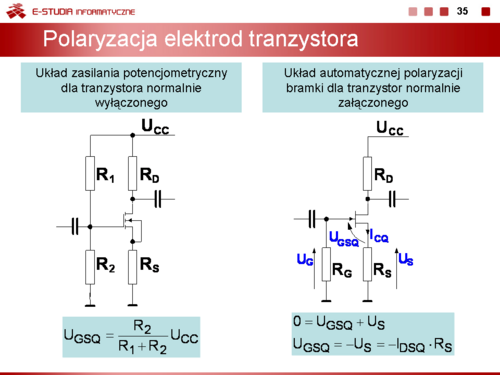
W układzie zasilania potencjometrycznym napięcie polaryzujące bramkę ma tę samą polaryzację co napięcie zasilania i ma wartość: | W układzie zasilania potencjometrycznym napięcie polaryzujące bramkę ma tę samą polaryzację co napięcie zasilania i ma wartość: | ||
<math> | <math>U_{GSQ}=\frac{R_2}{R_1+R_2}U_{CC}</math> | ||
Dla układu z automatyczna polaryzacją bramki napięcie bramka-źródło ustalające punkt pracy ma przeciwną polaryzację niż napięcie zasilania. Dla tego obwodu można napisać | Dla układu z automatyczna polaryzacją bramki napięcie bramka-źródło ustalające punkt pracy ma przeciwną polaryzację niż napięcie zasilania. Dla tego obwodu można napisać | ||
<math> | <math>U_G=U_{GSQ}+U_S</math> | ||
<math> | <math>U_S=I_{DSQ}\cdot R_S</math> | ||
Prąd <math>I_{DSQ}\,</math> jest równy prądowi drenu w wybranym punkcie pracy dla <math>U_{GS} = U_{GSQ}</math>. Ponieważ prąd bramki w tranzystorze unipolarnym praktycznie nie płynie <math>(I_G = 0\, A)</math> to nawet kiedy rezystancja <math>R_G\,</math> będzie bardzo wielka (np. rzędu <math>1\, M\Omega\,</math>) spadek napięcia na niej także będzie równy <math>U_G = 0\, V</math>. | Prąd <math>I_{DSQ}\,</math> jest równy prądowi drenu w wybranym punkcie pracy dla <math>U_{GS} = U_{GSQ}</math>. Ponieważ prąd bramki w tranzystorze unipolarnym praktycznie nie płynie <math>(I_G = 0\, A)</math> to nawet kiedy rezystancja <math>R_G\,</math> będzie bardzo wielka (np. rzędu <math>1\, M\Omega\,</math>) spadek napięcia na niej także będzie równy <math>U_G = 0\, V</math>. | ||
| Linia 478: | Linia 478: | ||
Otrzymamy zatem następujące zależności | Otrzymamy zatem następujące zależności | ||
<math> | <math>0=U_{GSQ}+U_S</math> | ||
<math> | <math>U_{GSQ}=-U_S=-I_{DSQ}\cdot R_S</math> | ||
Dobierając odpowiednia wartość rezystora RS możemy jednoznacznie ustalić punkt pracy tranzystora bez stosowania dodatkowego ujemnego źródła zasilania. | Dobierając odpowiednia wartość rezystora RS możemy jednoznacznie ustalić punkt pracy tranzystora bez stosowania dodatkowego ujemnego źródła zasilania. | ||
| Linia 499: | Linia 499: | ||
Istotnymi parametrami tych obwodów są podobnie jak w układach z tranzystorami bipolarnymi: | Istotnymi parametrami tych obwodów są podobnie jak w układach z tranzystorami bipolarnymi: | ||
<math> | <math>r_{WE}=\frac{u_1}{i_1}\bigg|_{i_2=0}</math> impedancja wejściowa, | ||
<math> | <math>r_{WY}=\frac{u_2}{i_2}\bigg|_{u_1=0}</math> impedancja wyjściowa, | ||
<math> | <math>k_{U}=\frac{u_2}{u_1}\bigg|_{i_2=0}</math> wzmocnienie napięciowe. | ||
|} | |} | ||
| Linia 512: | Linia 512: | ||
z parametrami w postaci uniwersalnej. | z parametrami w postaci uniwersalnej. | ||
<math> | <math>i_G=\frac{u_{GS}}{r_{GS}},\, r_{DS}\to \infty ,\, i_G\to 0</math> | ||
<math> | <math>i_D=u_{GS}\cdot S+u_{DS}\cdot \frac{1}{r_{DS}}</math> | ||
|} | |} | ||
| Linia 522: | Linia 522: | ||
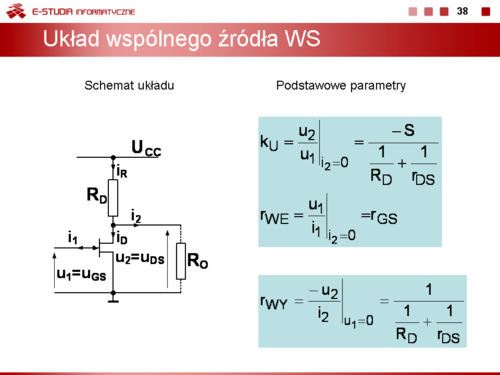
|valign="top"|W układzie wspólnego źródła, który jest odpowiednikiem układu wspólnego emitera dla tranzystorów bipolarnych, można zapisać: | |valign="top"|W układzie wspólnego źródła, który jest odpowiednikiem układu wspólnego emitera dla tranzystorów bipolarnych, można zapisać: | ||
<math> | <math>u_1=u_{GS}</math> | ||
<math> | <math>u_2=u_{DS}</math> | ||
<math> | <math>i_1=i_G\to 0\, A</math> | ||
<math> | <math>i_R=i_D+i_2</math> | ||
<math> | <math>i_R\cdot R_D+u_2=0</math> | ||
Podstawiając <math> | Podstawiając <math>i_2 = 0</math> możemy obliczyć wzmocnienie napięciowe i rezystancję wejściową układu WS | ||
<math> | <math>k_U=\frac{u_2}{u_1}\bigg|_{i_2=0}= \frac{-S}{\frac{1}{R_D}+\frac{1}{r_{DS}}}</math> | ||
<math> | <math>r_{WE}=\frac{u_1}{i_1}\bigg|_{i_2=0}= r_{GS}</math> | ||
Znak minus we wzorze na wzmocnienie napięciowe oznacza odwrócenie fazy sygnału wyjściowego w stosunku do sygnału wejściowego. | Znak minus we wzorze na wzmocnienie napięciowe oznacza odwrócenie fazy sygnału wyjściowego w stosunku do sygnału wejściowego. | ||
| Linia 542: | Linia 542: | ||
Jeżeli jest <math>i_2\neq 0</math> to uwzględniając warunek <math>u_1 = 0</math> można napisać | Jeżeli jest <math>i_2\neq 0</math> to uwzględniając warunek <math>u_1 = 0</math> można napisać | ||
<math> | <math>\frac{-u_2}{R_D}-i_2=0\cdot S+\frac{u_2}{r_{DS}}</math> | ||
Przekształcając to równanie wyznacza się rezystancję wyjściową układu wspólnego źródła WS | Przekształcając to równanie wyznacza się rezystancję wyjściową układu wspólnego źródła WS | ||
<math> | <math>r_{WY}=\frac{-u_2}{i_2}\bigg|_{u_1=0}= \frac{1}{\frac{1}{R_D}+\frac{1}{r_{DS}}}</math> | ||
Uzyskane wzory są podobne do zależności opisujących układ wspólnego emitera. | Uzyskane wzory są podobne do zależności opisujących układ wspólnego emitera. | ||
| Linia 558: | Linia 558: | ||
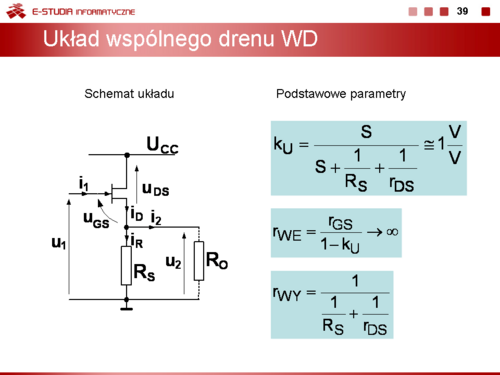
|valign="top"|Dla układu wspólnego drenu WD, postępując podobnie jak dla układu wspólnego źródła można napisać | |valign="top"|Dla układu wspólnego drenu WD, postępując podobnie jak dla układu wspólnego źródła można napisać | ||
<math> | <math>i_1=i_G</math> | ||
<math> | <math>i_D=i_R+i_2</math> | ||
<math> | <math>u_1-u_2=u_{GS}</math> | ||
<math> | <math>u_2+u_{DS}=0</math> | ||
<math> | <math>i_R\cdot R_S=u_2</math> | ||
Przyjmując <math>i_2 = 0</math> można napisać | Przyjmując <math>i_2 = 0</math> można napisać | ||
<math> | <math>\frac{u_2}{R_S}=S\cdot (u_1-u_2)-\frac{u_2}{r_{DS}}</math> | ||
Po przekształceniu tej zależności wzmocnienie napięciowe <math>k_U\,</math> układu wspólnego źródła jest równe | Po przekształceniu tej zależności wzmocnienie napięciowe <math>k_U\,</math> układu wspólnego źródła jest równe | ||
<math> | <math>k_U=\frac{S}{S+\frac{1}{R_S}+\frac{1}{r_{DS}}}\cong 1\frac{V}{V}</math> | ||
Warto zauważyć, że <math>k_U\,</math> ma zawsze wartość mniejszą od 1. | Warto zauważyć, że <math>k_U\,</math> ma zawsze wartość mniejszą od 1. | ||
Rezystancja wejściowa po uwzględnieniu zależności <math> | Rezystancja wejściowa po uwzględnieniu zależności <math>u_1-u_2=i_1\cdot r_{GS}</math> jest równa | ||
<math> | <math>r_{WE}=\frac{r_{GS}}{1-k_U}\to \infty</math> | ||
Przy założeniu, że <math>i_2\neq 0</math> i <math>u_1 = 0</math> rezystancja wyjściowa jest równa | Przy założeniu, że <math>i_2\neq 0</math> i <math>u_1 = 0</math> rezystancja wyjściowa jest równa | ||
<math> | <math>r_{WY}=\frac{1}{\frac{1}{R_S}+\frac{1}{r_{DS}}}</math> | ||
|} | |} | ||
| Linia 592: | Linia 592: | ||
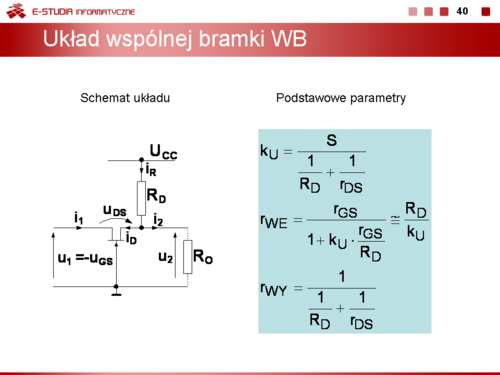
|valign="top"|Dla układu wspólnej bramki WG zależności na wzmocnienie napięciowe, rezystancję wejściową i wyjściową są podobne do tych jakie uzyskano dla układu wspólnej bazy. | |valign="top"|Dla układu wspólnej bramki WG zależności na wzmocnienie napięciowe, rezystancję wejściową i wyjściową są podobne do tych jakie uzyskano dla układu wspólnej bazy. | ||
<math> | <math>k_U=\frac{S}{\frac{1}{r_{DS}}+\frac{1}{R_S}}</math> | ||
<math> | <math>r_{WE}=\frac{r_{GS}}{1+k_U\cdot \frac{r_{GS}}{R_D}}}\cong \frac{R_D}{k_U}</math> | ||
<math> | <math>r_{WY}=\frac{1}{\frac{1}{R_S}+\frac{1}{r_{DS}}}</math> | ||
Cecha charakterystyczną jest znaczne zmniejszenie rezystancja wejściowej wzmacniacza. | Cecha charakterystyczną jest znaczne zmniejszenie rezystancja wejściowej wzmacniacza. | ||
Wersja z 08:56, 28 sie 2023
 |
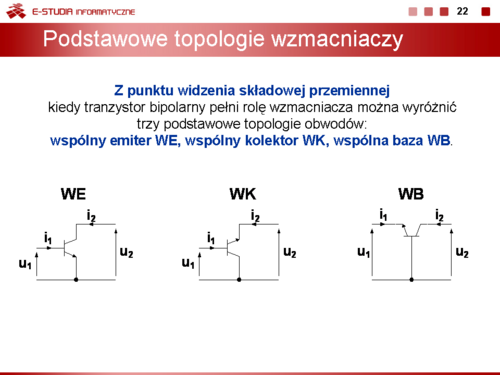
Podstawowe topologie połączeń elementów półprzewodnikowych: punkt pracy, stany pracy
|
 |
Przy połączeniu równoległym suma prądów jest stała i równa I.
Podobnie jak przy połączeniu szeregowym prąd IQ oraz napięcie UQ określają współrzędne punktu pracy elementu nieliniowego. |
 |
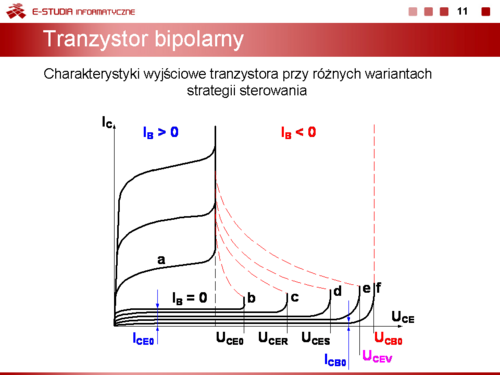
Warianty sterowania |
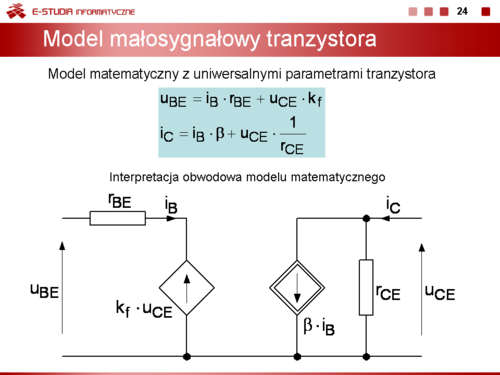 |
Przy wyznaczaniu tych parametrów stosuje się małosygnałowy model tranzystora bipolarnego opisany równaniami macierzy hybrydowej z parametrami w postaci uniwersalnej.
|
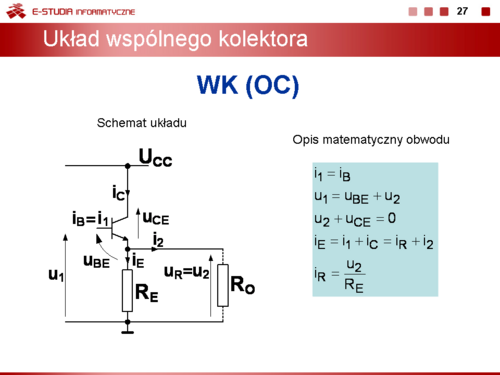 |
Dla układu wspólnego kolektora WK, często nazywanego także wtórnikiem emiterowym można zapisać
|
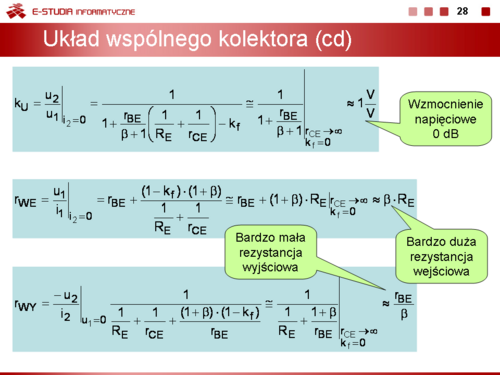 |
Wzmocnienie napięciowe tego układu jest bliskie, ale zawsze mniejsze od jedności
Rezystancja wejściowa jest równa
a rezystancja wyjściowa
|
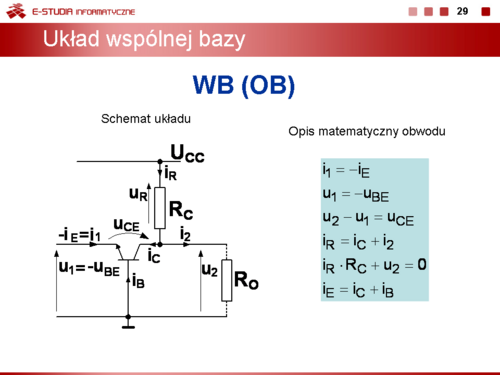 |
Dla układu wspólnej bazy WB można zapisać:
|
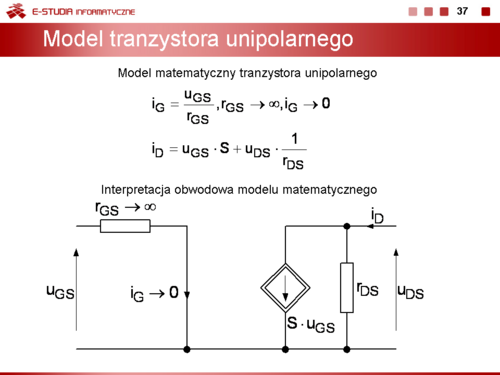 |
Przy wyznaczaniu tych parametrów można wykorzystać małosygnałowy model tranzystora unipolarnego opisany równaniami macierzy admitancyjnej
z parametrami w postaci uniwersalnej.
|
Bibliografia
- Kaźmierkowski M. P., Matysik J. T.: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2005
- Baranowski J., Nosal Z.: Układy elektroniczne cz. I. Układy analogowe liniowe, Wydawnictwa Naukowo-Techniczne, Warszawa 1998