PEE Moduł 11: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 34: | Linia 34: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd5.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd5.png|thumb|500px]] | ||
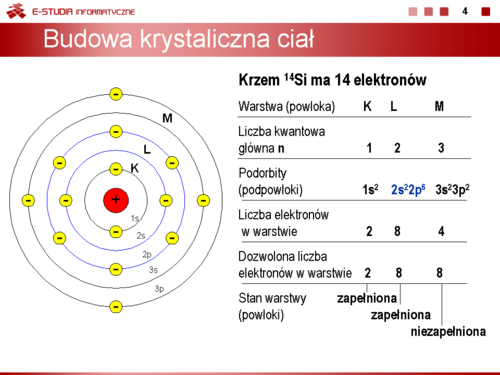
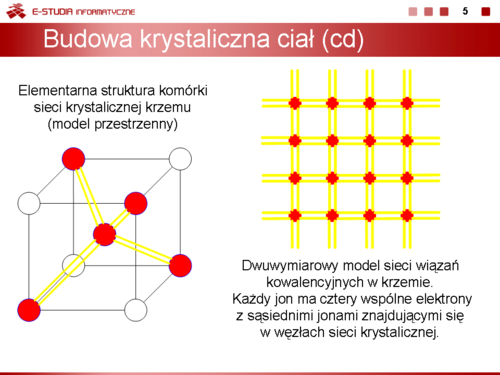
|valign="top"|W elektronice stosuje się krzem o strukturze krystalicznej, w której wszystkie atomy w całej objętości materiału są uporządkowane i związane ze sobą siłami wiązań atomowych tzw. kowalencyjnych i tworzą tzw. siatkę krystaliczną. Strukturę krystaliczną krzemu, którą często nazywamy strukturą diamentu przedstawiono na slajdzie 5. Dla temperatury zera bezwzględnego, kiedy siatka krystaliczna nie wykonuje żadnych ruchów w każdym narożniku sześcianu o boku około <math>5,4 | |valign="top"|W elektronice stosuje się krzem o strukturze krystalicznej, w której wszystkie atomy w całej objętości materiału są uporządkowane i związane ze sobą siłami wiązań atomowych tzw. kowalencyjnych i tworzą tzw. siatkę krystaliczną. Strukturę krystaliczną krzemu, którą często nazywamy strukturą diamentu przedstawiono na slajdzie 5. Dla temperatury zera bezwzględnego, kiedy siatka krystaliczna nie wykonuje żadnych ruchów w każdym narożniku sześcianu o boku około <math>5,4 angstrem (1 angstrem = 10^{-10 }m)</math> są umieszczone nieruchome jądra atomów. Pomiędzy sąsiadującymi ze sobą jądrami krążą pary elektronów tworząc bardzo trwałe wiązanie atomowe przy czym, ponieważ w każdej chwili czasowej z każdym jądrem są związane cztery elektrony walencyjne struktura ta jest elektrycznie obojętna. Aby rozerwać wiązanie atomowe utworzone przez cztery elektrony walencyjne należy dostarczyć do siatki krystalicznej znacznej energii tzw. energii jonizacji. | ||
|} | |} | ||
| Linia 112: | Linia 112: | ||
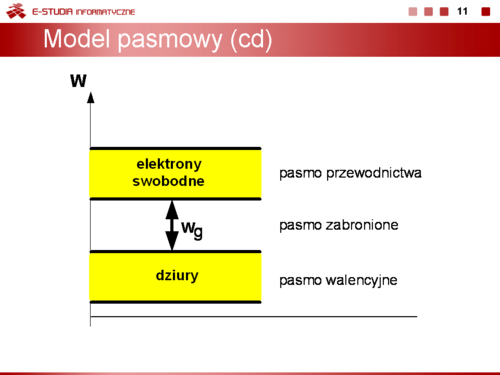
a zatem przeskok elektronu z pasma walencyjnego do pasma przewodnictwa jest bardzo trudny w realizacji ponieważ wymaga dostarczenia do elektronu dużej energii. | a zatem przeskok elektronu z pasma walencyjnego do pasma przewodnictwa jest bardzo trudny w realizacji ponieważ wymaga dostarczenia do elektronu dużej energii. | ||
W izolatorach tylko znikoma ilość elektronów przechodzi do pasma przewodnictwa i tworzy prąd elektryczny dlatego rezystywność izolatorów jest bardzo wielka | W izolatorach tylko znikoma ilość elektronów przechodzi do pasma przewodnictwa i tworzy prąd elektryczny dlatego rezystywność izolatorów jest bardzo wielka | ||
rzędu <math>10^{10} | rzędu <math>10^{10} - 10^{20} \Omega\cdot m</math>. | ||
Półprzewodniki, które w temperaturze T = 0 K są izolatorami, w temperaturze otoczenia 300 K wykazują właściwości przewodzące, ponieważ w tej temperaturze niektóre elektrony walencyjne przeskakują do pasma przewodzenia i tworzą prąd elektryczny. Ponieważ koncentracja atomów w ciałach stałych jest mniej więcej stała i porównywalna z liczbą Avogadra tzn. w <math>1\, m^3</math> jest około <math>5\cdot 10^{28}</math> atomów, to w temperaturze 300 K, dla <math>n_i = 10^{13}</math> tylko jeden na <math>5\cdot 10^{15}</math> atomów półprzewodnika jest zjonizowany. Oznacza to, że w paśmie przewodnictwa jest w <math>1\, m^3</math> około <math>10^{13}\,</math> elektronów swobodnych, które tworzą prąd elektryczny. Rezystywność ma w tym wypadku wartość około <math>10 - 10^5 \Omega \cdot m</math> i silnie zależy od temperatury. | |||
Na slajdzie w tabeli podano energię pasma zabronionego dla różnych materiałów półprzewodnikowych. | |||
Półprzewodniki, które w temperaturze T = 0 K są izolatorami, w temperaturze otoczenia 300 K wykazują właściwości przewodzące, ponieważ w tej temperaturze niektóre elektrony walencyjne przeskakują do pasma przewodzenia i tworzą prąd elektryczny. Ponieważ koncentracja atomów w ciałach stałych jest mniej więcej stała i porównywalna z liczbą Avogadra tzn. w <math>1 cm^3</math> jest około <math>6\cdot 10^2^3</math> atomów, to w temperaturze 300 K tylko jeden na <math>6\cdot 10^1^2</math> atomów półprzewodnika jest zjonizowany. Oznacza to, że w paśmie przewodnictwa jest w <math>1 cm^3</math> około <math>10^1^4</math> elektronów swobodnych, które tworzą prąd elektryczny. Rezystywność ma w tym wypadku wartość około <math>10-10^5 \Omega\cdot m</math> i silnie zależy od temperatury. | Półprzewodniki, które w temperaturze T = 0 K są izolatorami, w temperaturze otoczenia 300 K wykazują właściwości przewodzące, ponieważ w tej temperaturze niektóre elektrony walencyjne przeskakują do pasma przewodzenia i tworzą prąd elektryczny. Ponieważ koncentracja atomów w ciałach stałych jest mniej więcej stała i porównywalna z liczbą Avogadra tzn. w <math>1 cm^3</math> jest około <math>6\cdot 10^2^3</math> atomów, to w temperaturze 300 K tylko jeden na <math>6\cdot 10^1^2</math> atomów półprzewodnika jest zjonizowany. Oznacza to, że w paśmie przewodnictwa jest w <math>1 cm^3</math> około <math>10^1^4</math> elektronów swobodnych, które tworzą prąd elektryczny. Rezystywność ma w tym wypadku wartość około <math>10-10^5 \Omega\cdot m</math> i silnie zależy od temperatury. | ||
W metalach pasmo walencyjne i przewodnictwa nakładają się na siebie. Oznacza to, | W metalach pasmo walencyjne i przewodnictwa nakładają się na siebie. Oznacza to, | ||
że w metalu nawet bez dostarczania energii z zewnątrz istnieją elektrony swobodne. Ponieważ koncentracja atomów w przewodnikach jest podobnie jak w półprzewodnikach rzędu <math>6\cdot 10^2^3</math>, a z jednego atomu jeden lub dwa elektrony walencyjne znajdują się | że w metalu nawet bez dostarczania energii z zewnątrz istnieją elektrony swobodne. Ponieważ koncentracja atomów w przewodnikach jest podobnie jak w półprzewodnikach rzędu <math>6\cdot 10^2^3</math>, a z jednego atomu jeden lub dwa elektrony walencyjne znajdują się | ||
w paśmie przewodnictwa to ładunek swobodny tworzący prąd elektryczny w przewodniku jest związany z ruchem bardzo wielkiej rzędu <math>10^2^4</math> w <math>1 cm^3</math> ilości elektronów. W tym wypadku rezystywność jest bardzo mała rzędu <math>10^- | w paśmie przewodnictwa to ładunek swobodny tworzący prąd elektryczny w przewodniku jest związany z ruchem bardzo wielkiej rzędu <math>10^2^4</math> w <math>1 cm^3</math> ilości elektronów. W tym wypadku rezystywność jest bardzo mała rzędu <math>10^{-8} \Omega \cdot m</math>. | ||
| Linia 157: | Linia 162: | ||
Mała w porównaniu z metalami i zależna silnie od temperatury koncentracja nośników | Mała w porównaniu z metalami i zależna silnie od temperatury koncentracja nośników | ||
w półprzewodnikach samoistnych powoduje, że nie są one szeroko stosowane w technice. Do budowy elementów i przyrządów półprzewodnikowych stosuje się powszechnie półprzewodniki niesamoistne inaczej domieszkowane. | w półprzewodnikach samoistnych powoduje, że nie są one szeroko stosowane w technice. Do budowy elementów i przyrządów półprzewodnikowych stosuje się powszechnie półprzewodniki niesamoistne inaczej domieszkowane. | ||
'''Przykład 1''' | |||
Przyjmując, że liczba atomów krzemu w <math>1\, m^3</math> jest rzędu <math>4,99\cdot 10^{28}</math>, szerokość pasma zabronionego 1,12 eV, koncentracja elektronów w paśmie przewodnictwa w temperaturze 300 K <math>n_{i1} = 1,5\cdot 10^{16}</math>, oszacować temperaturę w której koncentracja swobodnych elektronów osiągnie wartość <math>n_i = 10^{20}</math>, <math>k = 1,38\cdot 10^{-23} J/K</math>. | |||
Rozwiązanie: | |||
Zależności | |||
<math>\displaystyle n_i^2=n_i_1^2(\frac{T}{T_1})^3\cdot e ^{\displaystyle \frac{W_g(T-T_1)}{k\cdot T\cdot T_1}}</math> | |||
ma postać uwikłaną i nie można z niej wyznaczyć prostymi metodami temperatury T. Jeżeli jednak zauważymy, że dla temperatur <math>T > T_1</math> dominującym czynnikiem w równaniu jest czynnik ekspotencjalny to upraszczając w/w zależność otrzymujemy: | |||
<math>\displaystyle n_i^2\cong n_i_1^2\cdot e ^{\displaystyle \frac{W_g(T-T_1)}{k\cdot T\cdot T_1}}</math> | |||
<math>\displaystyle T\cong \frac{T_1}{\displaystyle 1-\frac{kT_1}{W_g}ln\frac{n_i^2}{n_{i1}^2}}=506K</math> | |||
Odp: T = 506 K <math>(233^\circ C)</math> | |||
|} | |} | ||
| Linia 196: | Linia 219: | ||
|valign="top"|'''Półprzewodniki niesamoistne''' | |valign="top"|'''Półprzewodniki niesamoistne''' | ||
Jeżeli do siatki krystalicznej półprzewodnika samoistnego (np. krzemu <math>S_i</math>) wprowadzimy przez domieszkowanie małe ilości pierwiastka pięciowartościowego, np.: antymonu <math>S_b</math>, arsenu <math>A_s</math> lub fosforu <math>P\,</math> to w niektórych węzłach atomy półprzewodnika zostaną zamienione atomami domieszki, | Jeżeli do siatki krystalicznej półprzewodnika samoistnego (np. krzemu <math>S_i</math>) wprowadzimy przez domieszkowanie małe ilości pierwiastka pięciowartościowego, np.: antymonu <math>S_b</math>, arsenu <math>A_s</math> lub fosforu <math>P\,</math> to w niektórych węzłach atomy półprzewodnika zostaną zamienione atomami domieszki. Nazywamy je donorami. Koncentrację domieszki donorowej oznaczmy przez <math>N_d\,</math>. Piąty elektron walencyjny donorów nie bierze udziału w wiązaniach kowalentnych sieci i staje się elektronem swobodnym. | ||
Na wykresie pasmowym półprzewodnika pojawia się dodatkowy poziom energetyczny tzw. poziom donorowy. W temperaturze otoczenia około 300 K wszystkie atomy domieszki są zjonizowane tzn. elektrony z pasma donorowego przeskoczyły do pasma przewodnictwa. | Na wykresie pasmowym półprzewodnika pojawia się dodatkowy poziom energetyczny tzw. poziom donorowy. W temperaturze otoczenia około 300 K wszystkie atomy domieszki są zjonizowane tzn. elektrony z pasma donorowego przeskoczyły do pasma przewodnictwa. | ||
Powstał półprzewodnik typu n. | Powstał półprzewodnik typu n. | ||
| Linia 224: | Linia 248: | ||
<math>N_n >> P_n</math> | <math>N_n >> P_n</math> | ||
Wprowadzenie domieszki donorowej spowodowało wielokrotny wzrost koncentracji elektronów swobodnych (donorowych) w paśmie przewodnictwa w stosunku do elektronów samoistnych powstających w procesie generacji termicznej par elektron-dziura. Jednocześnie zmniejszyła się koncentracja dziur w paśmie walencyjnym. | |||
|} | |} | ||
| Linia 230: | Linia 255: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd20.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd20.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Jeżeli do siatki krystalicznej półprzewodnika samoistnego (np. krzemu Si) wprowadzimy przez domieszkowanie małe ilości pierwiastka trójwartościowego, np.: glinu Al, indu In lub galu Ga to w niektórych węzłach atomy półprzewodnika zostaną zamienione atomami domieszki. Nazywamy je akceptorami. Koncentrację domieszki akceptorowej oznaczmy przez <math>P_a\,</math>. Brak czwartego elektronu walencyjnego dekompletuje jedno z wiązań kowalentnych w siatce krystalicznej. Występujący tu brak elektronu może być uzupełniony elektronem z sąsiedniego wiązania. Powstaje w ten sposób dziura, która może przemieszczać się w krysztale podobnie jak elektron walencyjny, ale w zasadzie niezależnie od niego. W tym wypadku w pobliżu pasma walencyjnego powstaje poziom energetyczny zwany poziomem akceptorowym. W temperaturze otoczenia około 300 K wszystkie atomy domieszki akceptorowej są zjonizowane. | ||
Jeżeli do siatki krystalicznej półprzewodnika samoistnego (np. krzemu Si) wprowadzimy przez domieszkowanie małe ilości pierwiastka trójwartościowego, np.: glinu Al, indu In lub galu Ga to w niektórych węzłach atomy półprzewodnika zostaną zamienione atomami domieszki, | |||
| Linia 249: | Linia 273: | ||
<math>P_p >> N_p </math> | <math>P_p >> N_p </math> | ||
W półprzewodniku typu p liczba dziur w paśmie walencyjnym jest znacznie większa od liczby elektronów w paśmie przewodnictwa. | W półprzewodniku typu p liczba dziur w paśmie walencyjnym jest znacznie większa od liczby elektronów w paśmie przewodnictwa. | ||
'''Przykład 2''' | |||
Płytka krzemu jest domieszkowana atomami akceptorowymi. Koncentracja domieszki <math>P_a = 3\cdot 10^{22} m^{-3}</math>. Jaka jest koncentracja dziur i elektronów swobodnych w temperaturze pokojowej <math>27^\circ C</math>, jeżeli koncentracja nośników samoistnych jest równa <math>n_i = 1,5\cdot 10^{16} m^{-3}</math>. | |||
Rozwiązanie: | |||
<math>P_P=P_a+p\approx P_a=3\cdot 10^{22}m^{-3}</math> | |||
<math>\displaystyle N_P=\frac{n_i^2}{P_a}=7,5\cdot 10^{22}m^{-3}</math> | |||
Wersja z 09:52, 16 sty 2007
 |
Podstawy fizyczne działania elementów półprzewodnikowych. |
 |
Tabela. Podstawowe materiały półprzewodnikowe |
 |
Przykłady defektów sieci krystalicznej |
 |
Obszar, w którym zachodzi bardzo silna (o kilka rzędów wielkości) zmiana koncentracji ładunku i typu przewodnictwa nazywa się złączem.
Szerokość złącza ma na ogół wymiar rzędu .
|
 |
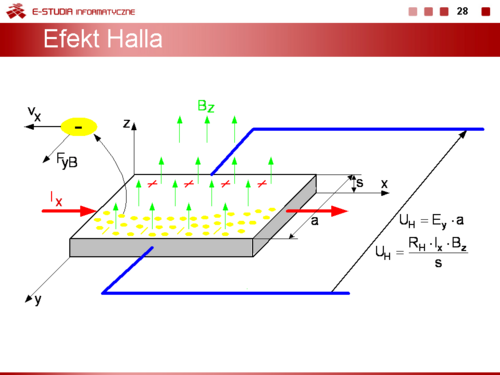
Przy niewielkich odchyleniach koncentracji nośników od stanu równowagi wypadkowa gęstość prądu elektronów i dziur jest równa:
|
| Literatura
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005 J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981 P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 |