PEE Moduł 12: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 133: | Linia 133: | ||
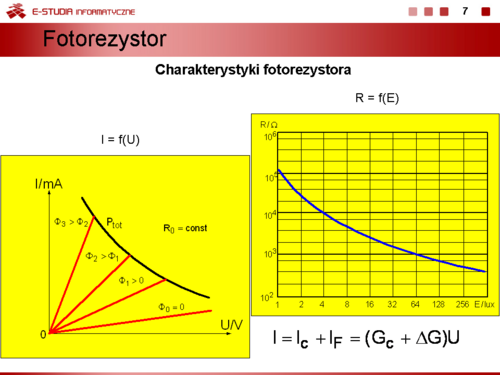
:<math>I_F\,</math> – prąd fotoelektryczny | :<math>I_F\,</math> – prąd fotoelektryczny | ||
:<math>G_c\,</math> – konduktancja ciemna | :<math>G_c\,</math> – konduktancja ciemna | ||
:<math>\ | :<math>\Delta G\,</math> – przyrost konduktancji pod wpływem oświetlenia. | ||
|} | |} | ||
| Linia 142: | Linia 141: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd8.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Piezorezystor''' to element, którego rezystancja zależy od siły nacisku, jaki wywierany jest w osi poprzecznej elementu. Często zastępuje, w przypadku niewielkich odkształceń, klasyczny tensometr wykonany ze stopu oporowego. Czułość piezorezystora jest definiowana jako | ||
:<math>\displaystyle k=\frac{\displaystyle\frac{R}{R_0}}{\displaystyle\frac{I}{I_0}}</math> | |||
gdzie | |||
:<math>R\,</math> – rezystancja płytki po przyłożeniu siły, | |||
:<math>R_0\,</math> – rezystancja początkowa (bez działania siły) | |||
:<math>l\,</math> – długość płytki po przyłożeniu siły | |||
:<math>l_0\,</math> – początkowa długość płytki (bez działania siły) | |||
Czułość piezorezystora jest bardzo duża 20-200, podczas gdy tensometr oporowy ma czułość tylko 2-6. Piezorezystory stosuje się jako czujniki w pomiarach sił oraz naprężeń statycznych i dynamicznych. | |||
|} | |} | ||
| Linia 149: | Linia 160: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd9.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd9.png|thumb|500px]] | ||
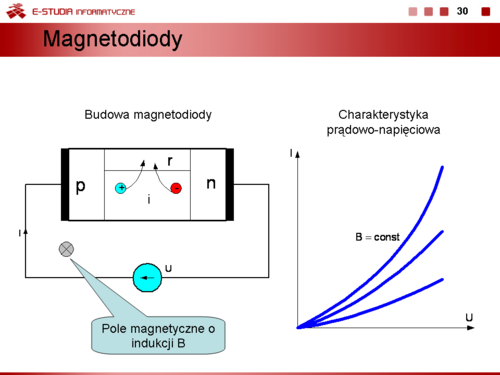
|valign="top"| | |valign="top"|'''Magnetorezystor''' nazywany także gaussotronem to rezystor o rezystancji zależnej od pola magnetycznego, w którym go umieszczono. Zależność rezystancji od indukcji magnetycznej opisana jest wzorem | ||
:<math>\displaystyle R_B=R_0\cdot \frac{\rho_B}{\rho_0}\cdot f(\mu, B, a, b)</math> | |||
gdzie <math>R_0, \rho_0</math> – rezystancja i rezystywność elementu przy <math>B = 0\, T</math> | |||
<math>R_B , \rho_B</math> – rezystancja i rezystywność elementu przy <math>B \neq 0\, T</math> | |||
<math>f(\mu, B, a, b)</math> – funkcja zależna od indukcji magnetycznej B i parametrów płytki: wymiarów a, b oraz ruchliwości nośników większościowych <math>\mu\,</math>. | |||
Podstawową charakterystyką magnetorezystora jest zależność <math>R_B = f(B)</math>. Magnetorezystory są wrażliwe na temperaturę co oznacza, że mają duży temperaturowy współczynnik rezystancji. Najczęściej nie należy przekraczać temperatury pracy płytki, <math>95^\circ C</math> . Typowe zastosowanie magnetorezystorów to czujniki do pomiaru indukcji magnetycznej, mocy i skutecznej wartości prądów odkształconych. | |||
|} | |} | ||
| Linia 156: | Linia 177: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd10.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd10.png|thumb|500px]] | ||
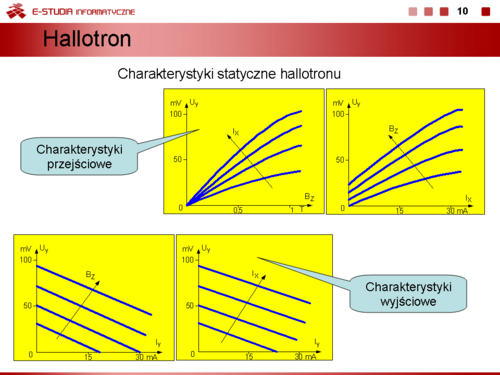
|valign="top"| | |valign="top"|'''Hallotrony''' są wykonane najczęściej w postaci płytek w kształcie krzyża z litych materiałów półprzewodnikowych lub z płytek mikowych z naparowanym półprzewodnikiem (Ge, InSb, InAs). Często wytwarza się je w technologii hybrydowych układów scalonych w jednej obudowie ze wzmacniaczem operacyjnym. Tego typu układy są szczególnie przydatne do pomiarów i badań pól magnetycznych, wielkości elektrycznych i nie elektrycznych oraz jako elementy mnożące i modulatory sygnałów wolnozmiennych. Właściwości elektryczne hallotronu opisują rodziny charakterystyk statycznych: przejściowych i wyjściowych. | ||
Charakterystyki statyczne przejściowe to funkcje zmian napięcia Halla <math>U_y\,</math> od parametru sterującego: poprzecznego pola magnetycznego <math>B_z\,</math> lub prądu przewodzenia <math>I_x\,</math>. Charakterystyki statyczne wyjściowe to funkcje zmian napięcia Halla <math>U_y\,</math> od prądu obciążenia <math>I_y\,</math> przy stałych parametrach sterujących <math>B_z\,</math>, <math>I_x\,</math>. | |||
|} | |} | ||
| Linia 163: | Linia 186: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd11.png|thumb|500px]] | ||
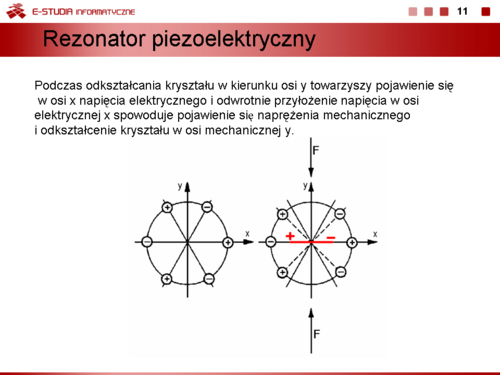
|valign="top"| | |valign="top"|'''Rezonatory piezoelektryczne''' wykorzystują zjawisko piezoelektryczne, które jest zjawiskiem odwracalnym. Polega ono na tym, że w krysztale półprzewodnikowym występują jednocześnie zjawiska elektryczne i mechaniczne. Podczas odkształcania kryształu w kierunku osi y towarzyszy pojawienie się w osi x napięcia elektrycznego i odwrotnie przyłożenie napięcia w osi elektrycznej spowoduje pojawienie się naprężenia mechanicznego i odkształcenie kryształu w osi mechanicznej. Na rysunku pokazano działanie siły ściskającej F, deformację komórki sieci krystalicznej i przesunięcie jonów powodujące powstanie dipola elektrycznego. | ||
Podstawowym materiałem do budowy rezonatorów piezoceramicznych jest kwarc. | |||
Jeżeli płytka kwarcowa jest zasilana napięciem zmiennym (powstaje zmienne pole elektryczne) o odpowiedniej częstotliwości to zaczyna ona drgać mechanicznie z częstotliwością rezonansową zależną od wymiarów geometrycznych i właściwości mechanicznych płytki. Amplituda drgań jest w tym wypadku znacznie większa od odkształceń jakie powstają, gdy częstotliwość napięcia zasilającego jest odstrojona od częstotliwości rezonansowej płytki. Drgający rezonator kwarcowy można traktować jak obwód rezonansowy. Poza rezonansem stanowi kondensator o pojemności zależnej od wymiarów geometrycznych płytki oraz powierzchni metalizowanych wyprowadzeń. Cechą charakterystyczną rezonatorów piezoelektrycznych jest stałość częstotliwości drgań rezonansowych w pewnym zakresie temperatur oraz powolne zmiany starzeniowe, dlatego stosuje się je często do budowy generatorów sinusoidalnych i filtrów pasmowych. | |||
|} | |} | ||
| Linia 170: | Linia 197: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd12.png|thumb|500px]] | ||
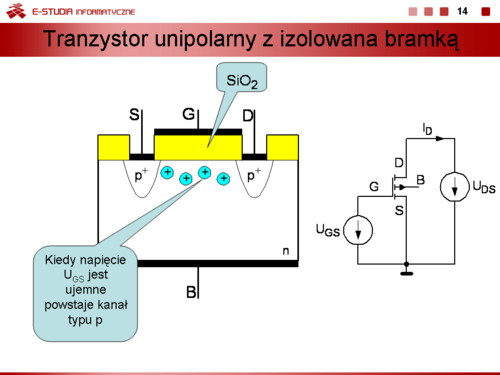
|valign="top"| | |valign="top"|'''Elementy bezzłączowe o efekcie powierzchniowym (polowym)''' | ||
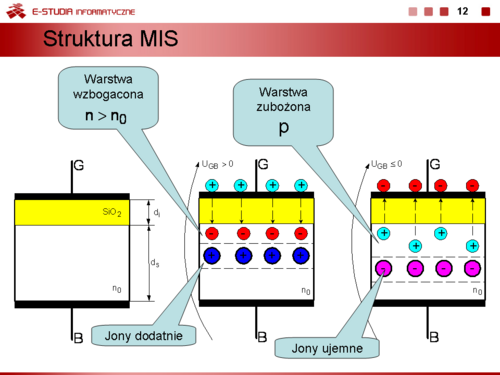
'''Struktura MIS (Metal-Insulator-Semiconductor)''' | |||
Na slajdzie przedstawiono strukturę MIS. Podłoże '''B''' (''Bulk'') o grubości <math>100-300 \mu m</math> stanowi często krzem samoistny lub słabo domieszkowany typu n lub p. Metalem, czyli elektrodą przewodzącą jest najczęściej cienka warstwa napylonego aluminium, a dielektrykiem warstwa tlenku <math>SiO_2\,</math>. Elektrodę metalową nazywamy bramką G (''Gate''). | |||
Załóżmy, że podłoże wykonano z półprzewodnika typu n o koncentracji elektronów <math>n_0\,</math>. | |||
Pomiędzy bramkę i podłoże przykładamy napięcie UGB wytwarzające słabe pole elektryczne. Jeżeli dla uproszczenia podłoże B umieścimy na potencjale zerowym, to napięcie UGB będzie mogło mieć wartość dodatnią lub ujemną. | |||
#Jeżeli <math>U_{GB} > 0\, V</math> to dodatnie pole elektryczne wnika do półprzewodnika i powoduje tzw. akumulację nośników tzn. przyciąganie nośników większościowych (elektronów) do warstwy przypowierzchniowej i utworzenie w niej ładunku przestrzennego ujemnego o wzbogaconej koncentracji <math>n > n_0</math>. Pod tą warstwą znajdują się nieruchome dodatnie jony domieszek tworzące warstwę zubożoną. Ponieważ nastąpiło rozdzielenie ładunków strukturę MIS (w tym wypadku, ponieważ dielektrykiem jest tlenek krzemu strukturę MOS, '''Metal-Oxide-Semiconductor''') można traktować jak kondensator o pojemności C. | |||
#<math>U_{GB} \le 0\, V</math>. Jeżeli zmniejszamy napięcie <math>U_{GB}\,</math> od wartości dodatnich do zera zmniejsza się ładunek indukowany w warstwie przypowierzchniowej i koncentracja elektronów powraca do wartości <math>n_0\,</math>. Jeżeli nadal będziemy zmniejszać napięcie <math>U_{GB}\,</math> i będzie spełniony warunek <math>U_{GB} < 0\, V</math> z warstwy przypowierzchniowej będą wypierane elektrony i pojawi się w niej ładunek mniejszościowy, czyli dziury. Nastąpi wzrost koncentracji dziur <math>p > p_0</math> w tej warstwie. W momencie, gdy <math>n < p</math> następuje zmiana znaku ładunku przestrzennego, czyli inwersja ładunku na którym kończą się linie pola elektrycznego. | |||
|} | |} | ||
| Linia 177: | Linia 215: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd13.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd13.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Głębokość wnikania pola, a zatem i grubość warstwy inwersyjnej, a także ładunek elektryczny zgromadzony w warstwie inwersyjnej zależy od wartości napięcia <math>U_GB\,</math> | ||
:<math>\displaystyle C_S=\frac{dQ_S}{dU_{GB}}</math> | |||
|} | |} | ||
Wersja z 10:55, 11 gru 2006
 |
Wykład 12. Podstawowe elementy półprzewodnikowe |
 |
Głębokość wnikania pola, a zatem i grubość warstwy inwersyjnej, a także ładunek elektryczny zgromadzony w warstwie inwersyjnej zależy od wartości napięcia
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |