GKIW Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 274: | Linia 274: | ||
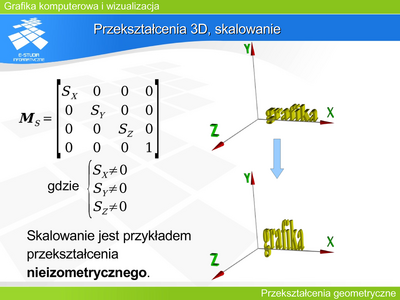
Warto zwrócić uwagę na fakt, że jeśli <math>S=S_X=S_Y=S_Z\neq 0</math> to skalowanie można opisać macierzą: | Warto zwrócić uwagę na fakt, że jeśli <math>S=S_X=S_Y=S_Z\neq 0</math> to skalowanie można opisać macierzą: | ||
: | :<math>M_{S1}=\begin{bmatrix} 1 & 0 & 0 & 0 \\0 & 1 & 0 & 0\\0 & 0 & 1 & 0 \\ 0 & 0 & 0 & \frac{1}{S} \end{bmatrix}</math> | ||
wtedy | |||
:<math>M_{S1}\cdot \begin{bmatrix} x_P \\y_P\\z_P \\ 1 \end{bmatrix}=\begin{bmatrix} x_P \\y_P\\z_P \\ \frac{1}{S} \end{bmatrix}</math> | |||
Ale wynik tej operacji nie jest znormalizowany. Zgodnie z przyjętymi wcześniej zasadami posługiwania się współrzędnymi jednorodnymi taka operacja jest w tym przypadku niezbędna. | |||
Zatem <math>\begin{bmatrix} x_P \\y_P\\z_P \\ \frac{1}{S} \end{bmatrix}\Longrightarrow \begin{bmatrix} S\cdot x_P \\S\cdot y_P\\S\cdot z_P \\ 1 \end{bmatrix}</math> co odpowiada skalowaniu ze współczynnikiem S. | |||
|} | |} | ||
| Linia 281: | Linia 289: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_25.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_25.png|400px]] | ||
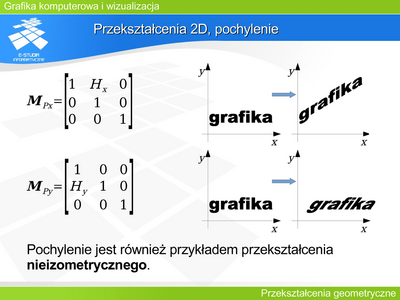
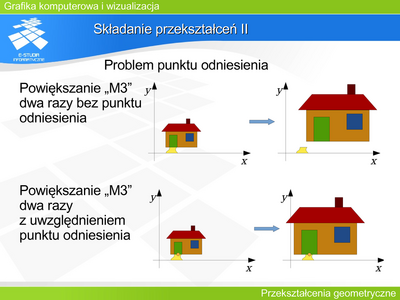
|valign="top"| | |valign="top"|'''Przekształcenie 3D, pochylenie''' | ||
Rysunek podaje macierz pochylenia trójwymiarowego dla z stałego, oraz przykład zniekształcenia sześcianu przez takie przekształcenie. Analogicznie można zaproponować przekształcenia i macierze je opisujące dla pochylenia przy stałym x oraz przy stałym y. | |||
|} | |} | ||
| Linia 287: | Linia 297: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_26.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_26.png|400px]] | ||
|valign="top"| | |valign="top"|'''Składanie przekształceń I''' | ||
Składanie przekształceń i operowanie macierzą wynikową pozwala realizować operacje efektywniej. | |||
Jeśli zatem <math>M_C\,</math> opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych <math>M_1,M_2,M_3\cdots M_N\,</math> (w takiej kolejności) to : | |||
:<math>M_C=M_N\cdot ... \cdot M_3\cdot M_2\cdot M_1\,</math> | |||
Oczywiście mnożenie macierzy i składanie przekształceń geometrycznych, jest operacją łączną ale nie jest operacją przemienną – złożenie najpierw translacji a potem obrotu jest innym przekształceniem niż złożenie najpierw obrotu a potem translacji. | |||
|} | |} | ||
| Linia 293: | Linia 311: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_27.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_27.png|400px]] | ||
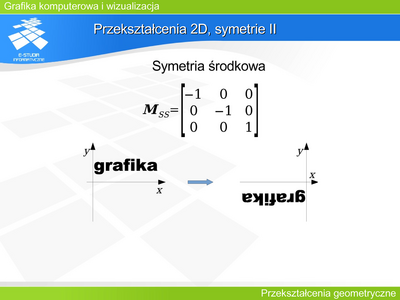
|valign="top"| | |valign="top"|'''Składanie przekształceń II''' | ||
Często pojawiającym się problemem w próbach implementacji przekształceń geometrycznych w grafice jest problem punktu odniesienia operacji. | |||
Skalowanie jest operacją zmieniającą proporcje wymiarów względem początku układu współrzędnych. Punkt [0,0,0] jest punktem stałym tego przekształcenia. Wyobraźmy sobie dwukrotne powiększenie pewnego obiektu (np. powiększenie domu jak na rysunku). Powiększenie dwukrotne oznacza nie tylko, że zwiększą się wymiary obiektu. Oznacza również, że każdy punkt obiektu zwiększy dwukrotnie odległość od początku układu współrzędnych. A przecież obiekt jest „osadzony” w pewnych realiach sceny – np. wejście do domu jest w określonym miejscu. Prosta realizacja skalowania prowadzi do pewnych konfliktów. Aby tego uniknąć należy wybrać punkt obiektu, który powinien zachować współrzędne – punkt odniesienia. A następnie zrealizować skalowanie względem tego punktu odniesienia. | |||
To jednak wymaga złożenia operacji: | |||
#Przesunięcie obiektu, aby punkt odniesienia znalazł się w początku układu współrzędnych. | |||
#Skalowanie obiektu. | |||
#Przesunięcie odwrotne do operacji 1. | |||
|} | |} | ||
| Linia 299: | Linia 328: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_28.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_28.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przekształcenie odwrotne''' | ||
Jeśli macierz <math>M\,</math> opisuje pewną transformację geometryczną, przekształcenie współrzędnych jest opisane równaniem <math>P'=M\cdot P</math> i jeśli istnieje przekształcenie odwrotne opisane macierzą <math>M^{-1}\,</math> to | |||
Oczywiście nie zawsze konieczne jest wyznaczanie macierzy odwrotnej, np. dla translacji o dany wektor przekształceniem odwrotnym będzie translacja o wektor przeciwny, dla obrotu o zadany kąt obrót wokół tej samej osi o kąt przeciwny itp. | |||
Ponieważ symetrie, translacja, obroty i skalowanie opisane odpowiednimi macierzami są operacjami odwracalnymi, to w bardzo prosty sposób można pokazać, że dowolna operacja będąca złożeniem dowolnego zestawu tych operacji, jest też operacją odwracalną. | |||
Jeśli zatem <math>M_C\,</math> opisuje całkowite przekształcenie będące wynikiem złożenia przekształceń elementarnych <math>M_C=M_N\cdot ... \cdot M_3\cdot M_2\cdot M_1\,</math> i jeśli każde z nich jest odwracalne to : | |||
:<math>M_C^{-1}=M_1^{-1}\cdot M_2^{-1}\cdot M_3^{-1}\cdot ...\cdot M_N^{-1}\,</math> | |||
|} | |} | ||
| Linia 305: | Linia 344: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_29.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_29.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przykład obrotu wokół prostej l I''' | ||
Zestaw podstawowych operacji obejmował obroty, ale tylko wokół osi układu współrzędnych. Obrót wokół dowolnej osi musi być zatem zrealizowany jako złożenie operacji. Można przyjąć założenie, że generalnie celem operacji wstępnych jest takie przekształcenie przestrzeni, aby zadana oś obrotu (prosta l na rysunku) pokryła się z wybraną osią układu współrzędnych. Przy czym przyjęty zwrot osi obrotu powinien być zgodny ze zwrotem osi okładu. Takie warunki pozwolą obrót o kąt <math>\varphi,</math> wokół zadanej osi zrealizować bezpośrednio jako obrót o kąt <math>\varphi,</math> wokół osi układu. | |||
Zadanie można rozwiązać na wiele sposobów. Przyjęto następujący zestaw operacji: | |||
#Przesunięcie, aby punkt <math>T_1\,</math> znalazł się w początku układu współrzędnych. | |||
#Obrót wokół osi OX. | |||
#Obrót wokół osi OY. Obroty (etap 2. i 3. ) zapewniają, że zadana oś obrotu (prosta l) pokryje się (z uwzględnieniem zwrotów) z osią OX układu współrzędnych. | |||
#Realizacja zadanego obrotu o kąt <math>\varphi,</math> wokół osi OX. | |||
#Obrót będący operacją odwrotną do operacji 3. | |||
#Obrót będący operacją odwrotną do operacji 2. | |||
#Przesunięcie odwrotne do przesunięcia 1. | |||
|} | |} | ||
| Linia 311: | Linia 363: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_30.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_30.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przykład obrotu wokół prostej l II''' | ||
Rysunek pokazuje wynik pierwszej operacji – przesunięcia. Zadana oś obrotu zawiera teraz przekątną prostopadłościanu o bokach A, B, C. Ułatwi to definicje kątów obrotu. | |||
|} | |} | ||
| Linia 317: | Linia 371: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_31.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_31.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przykład obrotu wokół prostej l III''' | ||
Po zrealizowaniu obrotu wokół OX prosta l znalazła się na płaszczyźnie XOZ. | |||
|} | |} | ||
| Linia 323: | Linia 379: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_32.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_32.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przykład obrotu wokół prostej l IV''' | ||
Po zrealizowaniu obrotu wokół OY prosta l pokryje się z osią OX układu współrzędnych. Jednocześnie odpowiednio dobrane operacje zapewniły zgodność zwrotów obu osi. | |||
|} | |} | ||
| Linia 329: | Linia 387: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_33.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_33.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przykład obrotu wokół prostej l V''' | ||
Teraz można wreszcie wykonać obrót o kąt <math>\varphi\,</math> wokół prostej l co, dzięki odpowiednim operacjom wstępnym, odpowiada obrotowi o kąt <math>\varphi\,</math> wokół osi OX układu współrzędnych. | |||
|} | |} | ||
| Linia 335: | Linia 395: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_34.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_34.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przykład obrotu wokół prostej l VI''' | ||
Następnymi etapami będą operacje przeciwne realizowane w odwrotnej kolejności. | |||
Macierz przekształcenia całkowitego jest iloczynem macierzy opisujących przekształcenia odpowiadające kolejnym przedstawionym etapom. | |||
|} | |} | ||
| Linia 341: | Linia 405: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_35.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_35.png|400px]] | ||
|valign="top"| | |valign="top"|'''Problemy dokładności obliczeń numerycznych I''' | ||
Problem dokładności obliczeń przy wykorzystaniu komputerów jest znany od kiedy istnieją komputery. Wiadomo, że liczby w komputerze są reprezentowane przez skończony ciąg cyfr. W przypadku liczb całkowitych stosowana jest reprezentacja stałopozycyjna i i jeśli rozpatrzymy arytmetykę binarną, to liczbie takiej odpowiada rozwinięcie dwójkowe o określonej długości słowa. Liczby rzeczywiste reprezentowane są zmiennopozycyjnie w postaci cechy i mantysy. Stosowanie określonej długości słowa do reprezentacji mantysy powoduje powstanie dokładności danej arytmetyki. Oznacza to, że reprezentacja liczb rzeczywistych obarczona jest zawsze pewnym błędem wynikającym z tej arytmetyki. Przeprowadzanie operacji graficznych wymaga często wielokrotnych obliczeń. Błędy reprezentacji (dokładność arytmetyki) mogą w widoczny sposób wpływać na efekt (graficzny !) obliczeń. Stosowane algorytmy powinny być tak realizowane, aby, o ile jest to możliwe, minimalizować te błędy. | |||
Rozpatrzmy przykład zegara, dla którego należy wyznaczyć położenie wskazówek. | |||
|} | |} | ||
| Linia 347: | Linia 415: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_36.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_36.png|400px]] | ||
|valign="top"| | |valign="top"|'''Problemy dokładności obliczeń numerycznych II''' | ||
Najprostszym rozwiązaniem jest algorytm iteracyjny powiększający w każdym kroku bieżący kąt o zadany przyrost. Niestety takie rozwiązanie prowadzi do powstania widocznych na tarczy zegara błędów już po kilkudziesięciu godzinach. | |||
|} | |} | ||
| Linia 353: | Linia 423: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_37.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_37.png|400px]] | ||
|valign="top"| | |valign="top"|'''Problemy dokładności obliczeń numerycznych III''' | ||
Jeśli przeanalizujemy algorytm naiwny, to okaże się, że wraz z powiększaniem wartości kąta dodajemy błędy. Błąd się nakłada wraz z postępowaniem obliczeń. | |||
|} | |} | ||
| Linia 359: | Linia 431: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_38.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_38.png|400px]] | ||
|valign="top"| | |valign="top"|'''Problemy dokładności obliczeń numerycznych IV''' | ||
Zadanie może być tak zrealizowane, aby błąd nie powiększał się. | |||
Realizując algorytm graficzny należy zawsze zwrócić uwagę na dokładność obliczeń numerycznych. Aby błąd zaokrągleń nie wpłynął na efekt obliczeń i nie zniweczył naszej pracy psując efekt końcowy. | |||
|} | |} | ||
| Linia 365: | Linia 441: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_39.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_39.png|400px]] | ||
|valign="top"| | |valign="top"|'''Kwaterniony I''' | ||
Kwaterniony (quaternions) są czterowymiarowym rozwinięciem liczb zespolonych. Zostały zaproponowane przez Williama Hamiltona w 1953 roku. | |||
:<math>i^2=j^2=k^2=ijk=-1</math> | |||
Dla dowolnego kwaternionu istnieje kwaternion przeciwny. | |||
Dla dowolnego kwaternionu różnego od zera istnieje kwaternion odwrotny. | |||
Suma dwóch kwaternionów jest kwaternionem. | |||
Iloczyn dwóch kwaternionów jest kwaternionem. | |||
|} | |} | ||
| Linia 371: | Linia 459: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_40.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_40.png|400px]] | ||
|valign="top"| | |valign="top"|'''Kwaterniony II''' | ||
Suma i iloczyn są zdefiniowane tak jak na rysunku. | |||
Dodawanie kwaternionów jest operacją łączną i przemienną. | |||
Mnożenie kwaternionów jest operacją łączną i '''nie jest''' operacją przemienną | |||
|} | |} | ||
| Linia 377: | Linia 471: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_41.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_41.png|400px]] | ||
|valign="top"| | |valign="top"|'''Kwaterniony III''' | ||
Kwaterniony są wykorzystywane w grafice komputerowej w związku z jedną operacją w przestrzeni trójwymiarowej: z obrotem punktu wokół dowolnie zdefiniowanej osi. Aby skorzystać z tej możliwości należy zdefiniować '''reprezentację punktu w postaci kwaternionu''' oraz '''jednostkowy wektor''' <math>\vec{u}</math> reprezentujący oś obrotu w przestrzeni. | |||
Biorąc pod uwagę kwaternion jednostkowy <math>q_u\,</math> związany z tym wektorem jednostkowym, można wyznaczyć kwaternion <math>Q_{Pu}\,</math> zgodnie z zaproponowanym wzorem. Kwaternion ten reprezentuje punkt będący obrazem w obrocie wokół osi wyznaczonej przez wektor <math>\vec{u}</math> o kąt <math>\varphi\,</math> . | |||
Porównując to rozwiązanie z zadaniem opisanym wcześniej widać prostotę operacji obrotu wykonywanej z wykorzystaniem kwaternionów. | |||
Większość obrotów realizowanych w grach komputerowych jest wykonywana w taki sposób. | |||
|} | |} | ||
Wersja z 13:36, 5 gru 2006

|

|
|

|
|
|

|
|
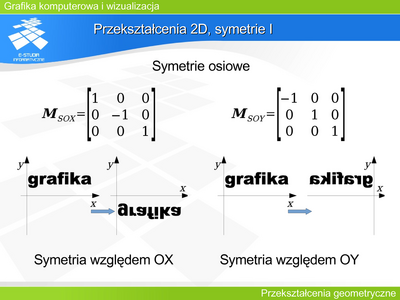
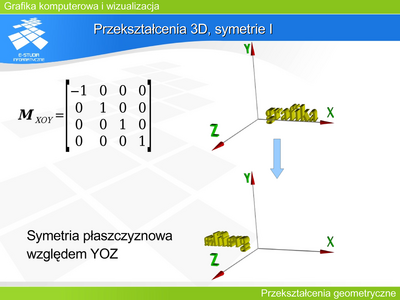
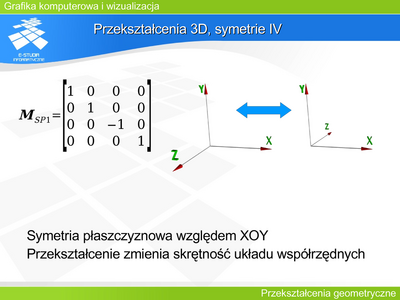
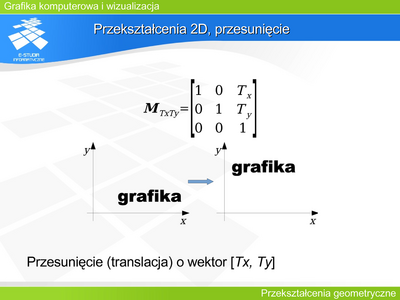
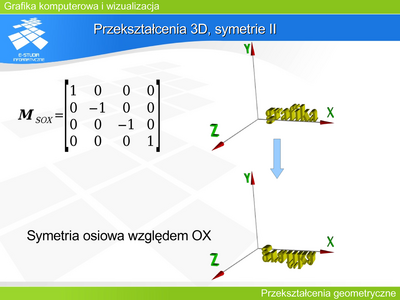
Przekształcenie 3D, symetrie II
Podobnie macierze opisujące symetrie osiowe względem pozostałych dwóch osi (OY i OZ) mają analogiczną postać ze zmienionymi znakami. |
|
|
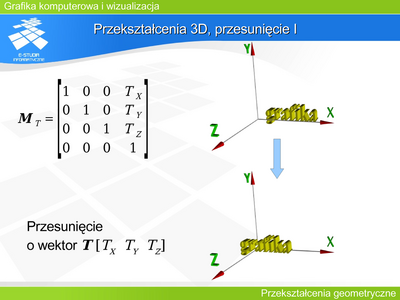
Przekształcenie 3D, przesunięcie I
Przesunięcie w układzie trójwymiarowym odbywa się w sposób analogiczny do przesunięcia na płaszczyźnie. |

|
|
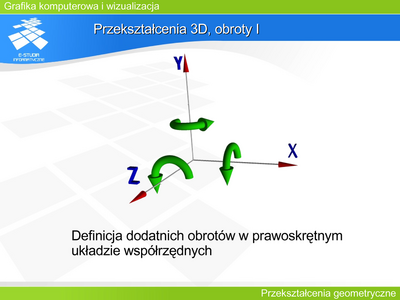
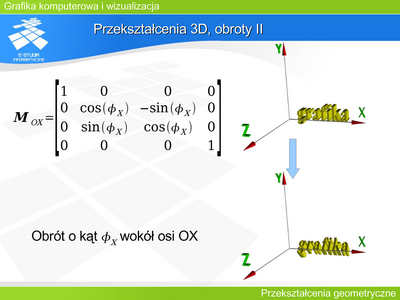
Przekształcenie 3D, obroty II
Obiekt na rysunku został obrócony o kat wokół osi OX. |
|
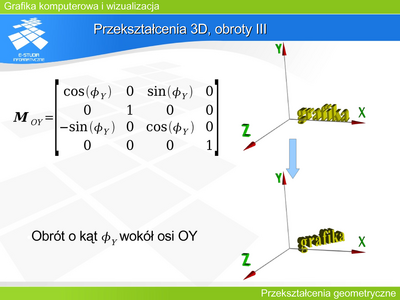
Przekształcenie 3D, obroty III
Obiekt na rysunku został obrócony o kat wokół osi OY |
|
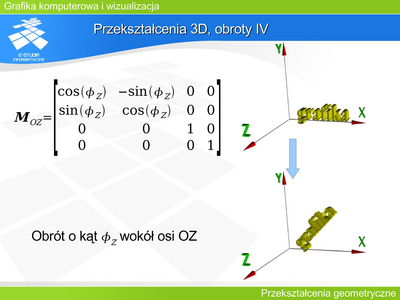
Przekształcenie 3D, obroty IV
Obiekt na rysunku został obrócony o kat wokół osi OZ. |

|
Przykład obrotu wokół prostej l III
Po zrealizowaniu obrotu wokół OX prosta l znalazła się na płaszczyźnie XOZ. |

|
Przykład obrotu wokół prostej l IV
Po zrealizowaniu obrotu wokół OY prosta l pokryje się z osią OX układu współrzędnych. Jednocześnie odpowiednio dobrane operacje zapewniły zgodność zwrotów obu osi. |

|
Przykład obrotu wokół prostej l V
Teraz można wreszcie wykonać obrót o kąt wokół prostej l co, dzięki odpowiednim operacjom wstępnym, odpowiada obrotowi o kąt wokół osi OX układu współrzędnych. |

|
Kwaterniony II
Suma i iloczyn są zdefiniowane tak jak na rysunku. Dodawanie kwaternionów jest operacją łączną i przemienną. Mnożenie kwaternionów jest operacją łączną i nie jest operacją przemienną |

|