GKIW Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 128: | Linia 128: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_7.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_7.png|400px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 138: | Linia 135: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_8.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_8.png|400px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 162: | Linia 153: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_11.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_11.png|400px]] | ||
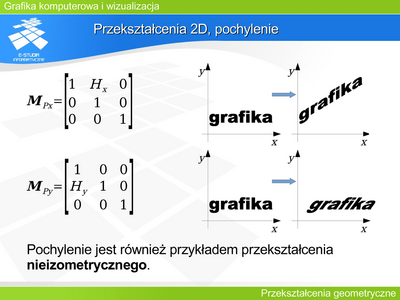
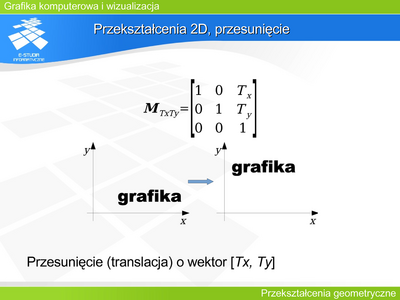
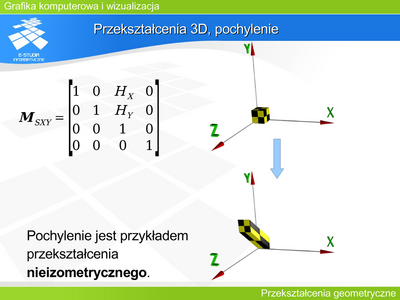
|valign="top"| | |valign="top"|'''Przekształcenie 2D, pochylenie''' | ||
Pochylenie jest rzadziej stosowanym przekształceniem. Daje możliwość zniekształcenia figury. Nie zachowuje odległości punktów. Figura i jej obraz w tym przekształceniu nie są podobne. | |||
|} | |} | ||
| Linia 168: | Linia 162: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_12.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_12.png|400px]] | ||
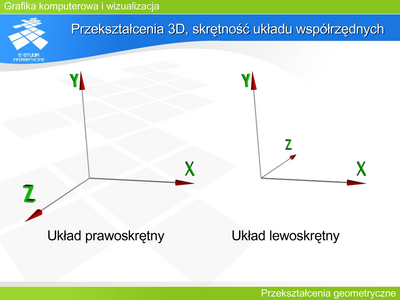
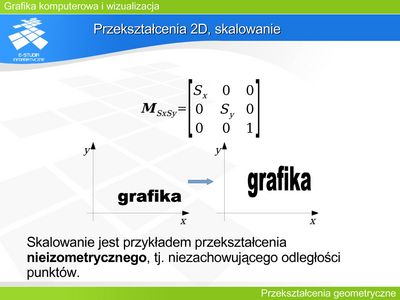
|valign="top"| | |valign="top"|'''Przekształcenie 3D, skrętność układu współrzędnych''' | ||
Możliwe są dwa ustawienia osi trójwymiarowego układu współrzędnych. Najczęściej do opisu położenia obiektów na scenie (w przestrzeni obiektu) stosowany jest układ prawoskrętny. Natomiast w operacjach związanych z rzutowaniem układ lewoskrętny. Wybór układu współrzędnych dla operacji rzutowania jest konsekwencją naturalnego rozumienia odległości obiektu od obserwatora. Jeśli osie OX i OY zdefiniują układ współrzędnych na rzutni (utożsamianej z płaszczyzną XOY) (pozioma oś OX skierowana w prawo i pionowa oś OY skierowana do góry), to kierunek wzrostu odległości od obserwatora wskaże oś OZ. Tak zdefiniowany układ współrzędnych będzie układem lewoskrętnym. | |||
Niech położenie punktu o współrzędnych <math>(x_p, y_p, z_p)</math> w przestrzeni trójwymiarowej reprezentuje wektor P : | |||
:<math>\begin{bmatrix} x_P \\y_P \\ z_P\\1 \end{bmatrix}</math> | |||
Jeśli macierz M opisuje pewną transformację geometryczną w przestrzeni 3D, to operację tę można opisać następująco: | |||
:<math>P'=M\cdot P</math> | |||
czyli: | |||
:<math>\begin{bmatrix} x_P^{'} \\y_P^{'} \\z_P^{'} \\ 1 \end{bmatrix}=M\cdot \begin{bmatrix} x_P \\y_P \\z_P \\ 1 \end{bmatrix}</math> | |||
gdzie P' opisuje położenie punktu po przekształceniu. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji. | |||
Operacje w przestrzeni 3D opisuje macierz 4x4 w przestrzeni 4D | |||
|} | |} | ||
| Linia 180: | Linia 193: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_14.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_14.png|400px]] | ||
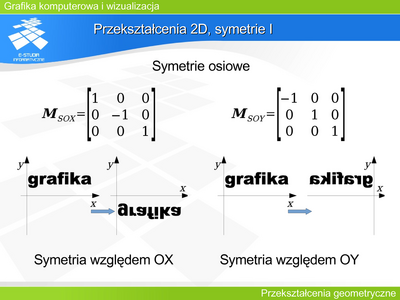
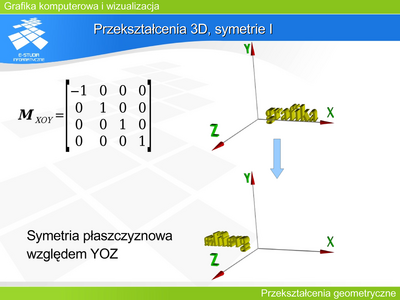
|valign="top"| | |valign="top"|'''Przekształcenie 3D, symetrie I''' | ||
Macierze opisujące symetrie płaszczyznowe względem pozostałych dwóch płaszczyzn (XOY i YOZ) mają analogiczną postać ze zmienionym znakiem przy 1 w odpowiedniej kolumnie. | |||
|} | |} | ||
| Linia 186: | Linia 201: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_15.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_15.png|400px]] | ||
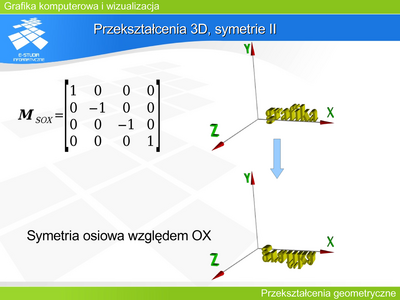
|valign="top"| | |valign="top"|'''Przekształcenie 3D, symetrie II''' | ||
Podobnie macierze opisujące symetrie osiowe względem pozostałych dwóch osi (OY i OZ) mają analogiczną postać ze zmienionymi znakami. | |||
|} | |} | ||
| Linia 198: | Linia 215: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_17.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_17.png|400px]] | ||
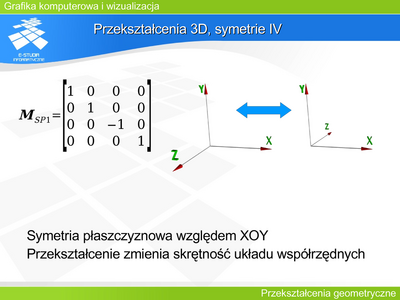
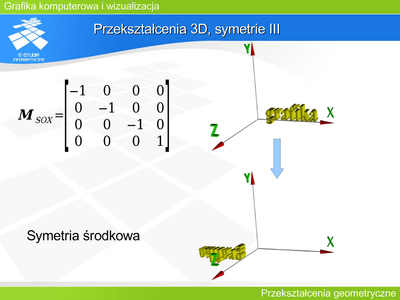
|valign="top"| | |valign="top"|'''Przekształcenie 3D, symetrie IV''' | ||
Jeżeli założyliśmy, że położenie obiektów sceny będzie opisywane w układzie prawoskrętnym, natomiast rzutowanie będzie rozpatrywane w układzie lewoskrętnym, to współrzędne tego samego punktu w obu układach będą się różniły znakiem przy współrzędnej z. Przeliczenie współrzędnych między układami zapewnia macierz symetrii płaszczyznowej względem XOY. | |||
|} | |} | ||
| Linia 204: | Linia 223: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_18.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_18.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przekształcenie 3D, przesunięcie I''' | ||
Przesunięcie w układzie trójwymiarowym odbywa się w sposób analogiczny do przesunięcia na płaszczyźnie. | |||
|} | |} | ||
| Linia 216: | Linia 237: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_20.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_20.png|400px]] | ||
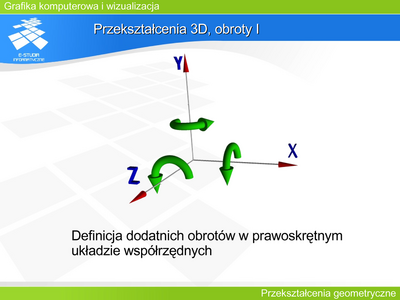
|valign="top"| | |valign="top"|'''Przekształcenie 3D, obroty I''' | ||
W układzie współrzędnych kartezjańskich trójwymiarowych zdefiniowanie obrotów wokół osi układu wymaga przyjęcia reguł uznawania obrotów za dodatnie. Najczęściej przyjmuje się konwencję, według której dodatnie obroty są zdefiniowane zgodnie z rysunkiem. | |||
|} | |} | ||
| Linia 222: | Linia 246: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_21.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_21.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przekształcenie 3D, obroty II''' | ||
Obiekt na rysunku został obrócony o kat <math>- 45^\circ</math> wokół osi OX. | |||
|} | |} | ||
| Linia 228: | Linia 254: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_22.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_22.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przekształcenie 3D, obroty III''' | ||
Obiekt na rysunku został obrócony o kat <math>45^\circ</math> wokół osi OY | |||
|} | |} | ||
| Linia 234: | Linia 262: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_23.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_23.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przekształcenie 3D, obroty IV''' | ||
Obiekt na rysunku został obrócony o kat <math>45^\circ</math> wokół osi OZ. | |||
|} | |} | ||
| Linia 240: | Linia 270: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_24.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M4_Slajd_24.png|400px]] | ||
|valign="top"| | |valign="top"|'''Przekształcenie 3D, skalowanie''' | ||
Warto zwrócić uwagę na fakt, że jeśli <math>S=S_X=S_Y=S_Z\neq 0</math> to skalowanie można opisać macierzą: | |||
: | |||
|} | |} | ||
Wersja z 12:56, 5 gru 2006

|

|
|

|
|
|

|
|
Przekształcenie 3D, symetrie II
Podobnie macierze opisujące symetrie osiowe względem pozostałych dwóch osi (OY i OZ) mają analogiczną postać ze zmienionymi znakami. |
|
|
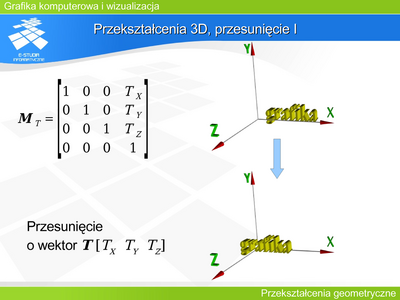
Przekształcenie 3D, przesunięcie I
Przesunięcie w układzie trójwymiarowym odbywa się w sposób analogiczny do przesunięcia na płaszczyźnie. |

|
|
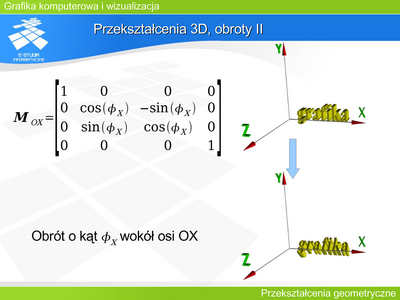
Przekształcenie 3D, obroty II
Obiekt na rysunku został obrócony o kat wokół osi OX. |
|
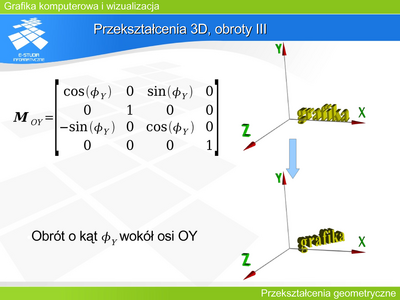
Przekształcenie 3D, obroty III
Obiekt na rysunku został obrócony o kat wokół osi OY |
|
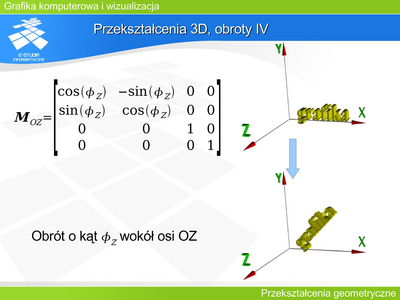
Przekształcenie 3D, obroty IV
Obiekt na rysunku został obrócony o kat wokół osi OZ. |
|
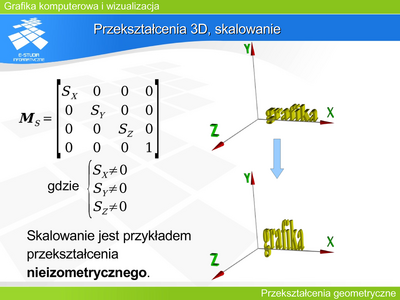
Przekształcenie 3D, skalowanie
Warto zwrócić uwagę na fakt, że jeśli to skalowanie można opisać macierzą: |
|

|
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|