GKIW Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 132: | Linia 132: | ||
|valign="top"|'''Mapowanie nierówności II''' | |valign="top"|'''Mapowanie nierówności II''' | ||
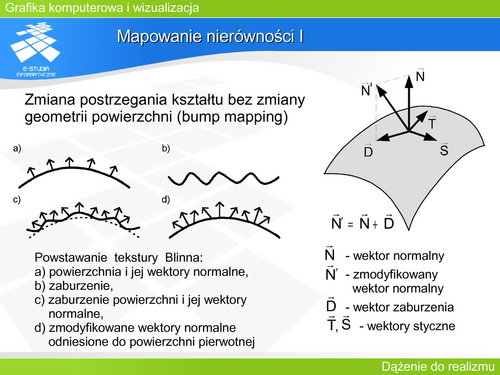
Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. Analogicznie niech <math>B(u,v)=[x_B(u,v), y_B(u,v), z_B(u,v)]</math> opisuje zaburzenie (teksturę). Wektor normalny <math>vec{N}\,</math> do powierzchni <math>S(u,v)\,</math> można wyznaczyć jako: | Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. Analogicznie niech <math>B(u,v)=[x_B(u,v), y_B(u,v), z_B(u,v)]</math> opisuje zaburzenie (teksturę). Wektor normalny <math>\vec{N}\,</math> do powierzchni <math>S(u,v)\,</math> można wyznaczyć jako: | ||
:<math>displaystyle </math> | :<math>\displaystyle \vec{N}=\frac{\partial S(u,v)}{\partial u}\times\frac{\partial S(u,v)}{\partial v}</math> | ||
Jeśli nałożymy teksturę na powierzchnię to powstanie powierzchnia zniekształcona | |||
:<math>S'(u,v)=S(u,v)+B(u,v)\cdot \vec{N}</math> | |||
Wektor normalny do tak otrzymanej powierzchni można wyznaczyć analogicznie. Przy czym różniczkując równanie zniekształconej powierzchni otrzymuje się: | |||
:<math>\displaystyle \frac{\partial S'(u,v)}{\partial u}=\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial u}</math> | |||
:<math>\displaystyle \frac{\partial S'(u,v)}{\partial v}=\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial v}</math> | |||
Blinn założył, że zaburzenie jest na tyle małe, że ostatnie wyrazy w tych równaniach można pominąć. Wtedy aproksymowany wektor normalny do zniekształconej powierzchni można opisać jako | |||
:<math>\displaystyle \vec{N}'\approx \left(\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}\ \right)\times \left(\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}\ \right)</math> | |||
to oznacza, że | |||
:<math>\vec{N}'=\vec{N}+\vec{D}</math> | |||
Przy czym <math>\vec{D}\,</math> jest wektorem zaburzenia: | |||
:<math>\vec{D}=\frac{\partial B(u,v)}{\partial u}\cdot \vec{S}-\frac{\partial B(u,v)}{\partial v}\cdot \vec{T}</math> | |||
gdzie <math>\vec{S}\,</math> i <math>\vec{T}\,</math> są wektorami stycznymi do powierzchni <math>S(u,v)\,</math>. | |||
Takie rozwiązanie daje bardzo prostą możliwość definicji wektora normalnego odkształconej powierzchni za pomocą wektorów zaburzenia. Wadą zaproponowanej przez Blinna metody jest aproksymacja wektora normalnego. Stąd powstało wiele różnych realizacji tej metody, wykorzystujących różne warianty uproszczenia. Znane są również próby aplikacji sprzętowych mapowania nierówności Blinna. | |||
|} | |} | ||
---- | ---- | ||
Wersja z 14:30, 4 gru 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |