GKIW Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 99: | Linia 99: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd9.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd9.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Parametryzacja powierzchni''' | ||
Prezentowane przykłady są parametryzacjami w przestrzeni obiektu. Pierwsza funkcja przekształca sferę obiektu na prostokąt tekstury. | |||
Drugi przykład jest funkcją przekształcającą powierzchnię boczną walca (powierzchnia obiektu) na prostokąt tekstury. | |||
|} | |} | ||
---- | ---- | ||
| Linia 105: | Linia 110: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd10.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd10.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Przykłady nakładania tekstur''' | ||
Prezentowane przykłady opisane są jako modele okresowe, przy czym w przypadku zdjęcia budynku Metropolita prostokąt tekstury jest nałożony dokładnie jeden raz, natomiast w pozostałych dwóch przypadkach prostokątny wzorzec jest powielany wielokrotnie. | |||
|} | |} | ||
---- | ---- | ||
| Linia 111: | Linia 119: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd11.png|thumb|500px]] | ||
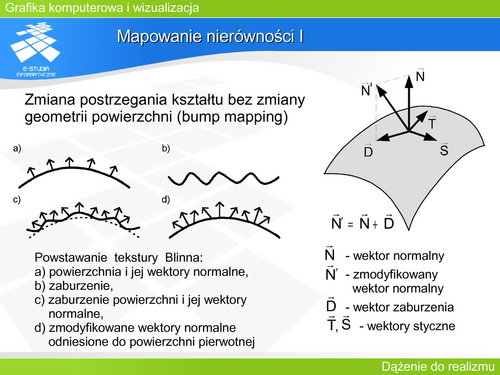
|valign="top"| | |valign="top"|'''Mapowanie nierówności I''' | ||
Modelowanie nierówności powierzchni jest przykładem tekstury dwuwymiarowej. Metoda ta (ang. bump mapping) została zaproponowana przez Blinna w 1978 roku. Pozwala uzyskiwać widok powierzchni o zmodyfikowanym kształcie bez modyfikowania samej geometrii powierzchni. | |||
Przy zastosowaniu tekstury Blinna zmianę kierunku wektora normalnego uzyskuje się przez dodatkową funkcje zaburzenia. Zmodyfikowany wektor normalny jest wykorzystywany w modelu oświetlenia, dzięki czemu są postrzegane lokalne zmiany oświetlenia. Oczywiście wektor zmieniony funkcją zaburzenia może, tak naprawdę, tworzyć dowolny kąt z powierzchnią obiektu, w związku z tym głównym problemem jest dobranie funkcji zaburzenia w taki sposób, aby zmiana wektora odpowiadała rzeczywistej zmianie kształtu powierzchni. | |||
|} | |} | ||
---- | ---- | ||
| Linia 117: | Linia 130: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd12.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Mapowanie nierówności II''' | ||
Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. Analogicznie niech <math>B(u,v)=[x_B(u,v), y_B(u,v), z_B(u,v)]</math> opisuje zaburzenie (teksturę). Wektor normalny <math>vec{N}\,</math> do powierzchni <math>S(u,v)\,</math> można wyznaczyć jako: | |||
:<math>displaystyle </math> | |||
|} | |} | ||
---- | ---- | ||
Wersja z 14:01, 4 gru 2006
 |
 |
 |
Mapowanie nierówności II
Niech opisuje parametrycznie powierzchnię, która będzie odkształcona. Analogicznie niech opisuje zaburzenie (teksturę). Wektor normalny do powierzchni można wyznaczyć jako: |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |