GKIW Moduł 8

---

---

Reakcja światła z materią Kolejnym problemem wymagającym rozwiązania, jeśli chcemy osiągnąć realizm rysunku, jest problem oświetlenia. Każda powierzchnia reaguje w jej właściwy sposób na padające na nią światło. Barwy, faktury i inne właściwości przedmiotów postrzegamy dzięki temu, że przedmioty te są oświetlone (lub same emitują światło). Symulacja tych zjawisk pozwala oddać realny wygląd elementów wirtualnej sceny. Można wyróżnić dwa niezależne przypadki: odbicie światła i przenikanie światła (dla materiałów przezroczystych). Oczywiście może zachodzić jeszcze pochłanianie, ale z punktu widzenia obserwatora jest to najmniej interesujący przypadek. Dla przypadku odbicia mówimy o odbiciu kierunkowym (lustrzanym) lub rozproszonym (dyfuzyjnym). W pierwszym przypadku padający promień odbija się pod kątem równym kątowi padania. W drugim przypadku odbicie może być widoczne pod dowolnym kątem. Analogiczna sytuacja może zajść dla przenikania światła.

---

Odbicie światła Odbicie rzeczywiste od powierzchni materiału jest zjawiskiem złożonym. Nawet dla najlepszych zwierciadeł promień odbity jest widoczny w pewnym niewielkim (niezerowym) kącie wokół kierunku odbicia idealnego (teoretycznego). W najprostszym przypadku wyróżnia się odbicie kierunkowe i rozproszone. Dla rzeczywistych powierzchni zawsze zachodzą oba przypadki i jednocześnie odbicie kierunkowe nie występuje w postaci idealnej. Dodatkowo może występować składowa odbicia powrotnego (współdrożnego) w kierunku, z jakiego padało światło. Można więc przyjąć rzeczywiste odbicie jako wypadkową 4 składowych (rysunek): rozproszonej, kierunkowej idealnej, kierunkowej rzeczywistej (ang. glossy – odbicia połysku), powrotnej. Analogiczne przypadki można wyróżnić rozpatrując załamanie promieni.

---

---

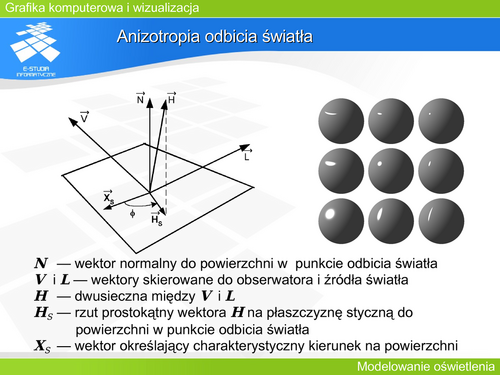
Anizotropia odbicia światła Anizotropia jest zjawiskiem polegającym na zależności właściwości fizycznych od charakterystycznych kierunków materiału. Pojęcie anizotropii optycznej jest najczęściej kojarzone z przechodzeniem światła przez kryształy i zjawiskiem dwójłomności. Spowodowane to jest zależnością współczynnika załamania światła od kierunku rozchodzenia się fali względem głównego przekroju kryształu. Wyróżnia się anizotropię naturalną (wykazuje ją większość kryształów) i anizotropię wymuszoną, spowodowaną takimi czynnikami zewnętrznymi jak działanie pól elektrycznych (zjawisko Kerra) i magnetycznych (zjawisko Cottona-Moutona) lub odkształcenia mechaniczne (ściskanie lub rozciąganie w zadanym kierunku). Z anizotropią mamy także do czynienia w przypadku odbicia promieniowania od powierzchni materiału. Wiele powierzchni, zarówno naturalnych, jak i uzyskanych w wyniku technologicznej obróbki odbija światło w sposób anizotropowy, zależny od kierunku jego padania – w sposób zależny od usytuowania powierzchni względem źródła światła. Dobrym przykładem powierzchni wykazującej naturalne właściwości anizotropowe jest powierzchnia drewna. Odbija ona światło zależnie od kata między kierunkiem padania a kierunkiem słojów przekroju. Powierzchnia metalu poddana obróbce mechanicznej (np. polerowaniu) będzie odbijała światło zależnie od kąta między padającym promieniem, a kierunkiem obróbki.

---

Model odbicia Phonga I Najstarszy, z praktycznie wykorzystywanych w grafice komputerowej modeli odbicia, zaproponował Bui Tuong Phong w 1975 roku Model Phonga jest modelem eksperymentalnym, nieuzasadnionym fizycznie i niespełniającym zasady zachowania energii. Mimo to jest, chyba, najczęściej stosowanym modelem odbicia w grafice komputerowej, gdyż pozwala szybko uzyskać rysunki o wystarczająco realistycznych barwach. W literaturze są opisywane metody poprawy modelu Phonga, aby spełniał on zasadę zachowania energii. Pierwszy składnik wzoru opisuje światło otoczenia (tła). Zakłada się, że jest ono rozproszone i bezkierunkowe oraz, że na skutek wielokrotnych odbić pada jednakowo pod wszystkimi kierunkami na rozpatrywane powierzchnie. Oczywiście również Ia jest jednakowe dla wszystkich obiektów. Drugi składnik opisuje odbicie rozproszone tak zwane lambertowskie. Powierzchnie matowe; rozpraszające światło jednakowo we wszystkich kierunkach opisane są prawem Lamberta, zgodnie z którym światłość promieniowania odbitego jest proporcjonalne do kosinusa kata padania. Oczywiście rzeczywiste powierzchnie rozpraszające zachowują się zgodnie z tym prawem tylko w pewnym zakresie kąta. Niemniej jednak taki opis odbicia rozproszonego jest najczęściej stosowany w modelach odbicia. Trzeci składnik opisuje odbicie kierunkowe (zwierciadlane). Maksimum natężenia promieniowania światłą odbitego występuje dla zerowego kąta  natomiast potęga n we wzorze charakteryzuje właściwości odbiciowe danego materiału. Warto jeszcze zwrócić uwagę na współczynnik tłumienia źródła światła. Wiemy z fizyki, że strumień światła pochodzący z punktowego źródła światła maleje z kwadratem odległości jaką przebywa. Zastosowanie tej reguły w modelu odbicia Phonga nie daje, niestety, w praktyce dobrych rezultatów. Dla dużych odległości od źródła zmiany są zbyt mało zauważalne, z kolei dla małych odległości zmiany występują zbyt szybko. Okazało się, że w praktyce dobre rezultaty można uzyskać dla współczynnika postaci $f_{att}=1/(c+r)$ gdzie c jest pewną stałą.

---

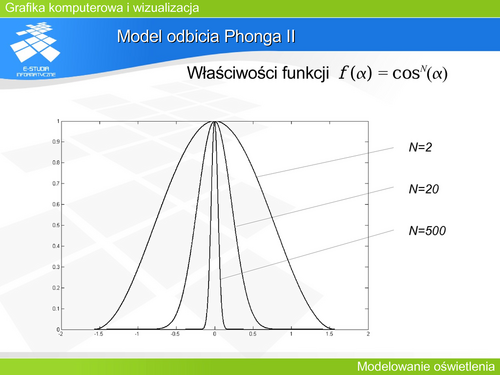
Model odbicia Phonga II Funkcja $co{s}^N(\alpha )$ opisuje odbicie kierunkowe (zwierciadlane) przy czy N charakteryzuje dany materiał (właściwości odbiciowe powierzchni). Warto zwrócić uwagę na właściwości tej funkcji. Idealne odbicie kierunkowe to takie, w którym odbicie występuje tylko dla zerowego kąta $\alpha$ (to znaczy poza tym kątem natężenie światła odbitego jest zerowe). Funkcja $co{s}^N(\alpha )$ opisuje taki przypadek dla N dążącego do nieskończoności. Zatem im większa wartość N tym bardziej powierzchnia zbliża się do powierzchni lustrzanej. Tym lepsze właściwości kierunkowe charakteryzują odbicie od tej powierzchni. W praktyce już dla $N$ rzędu kilkuset mamy do czynienia z dobrym lustrem.

---

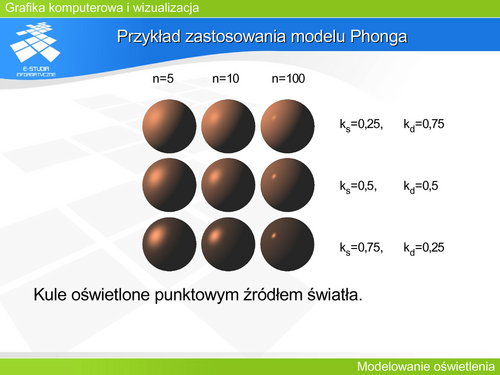
Przykład zastosowania modelu Phonga Na rysunku widać wpływ parametrów modelu odbicia Phonga na obraz odbicia światła na symulowanej powierzchni. Górny rząd charakteryzuje się przewagą odbicia rozproszonego, dolny – kierunkowego. Jednocześnie kolumny charakteryzują odbicie kierunkowe od lewej o złych parametrach odbicia kierunkowego (n=5) do prawej zbliżającej się do właściwości lustrzanych.

---

Podstawowe wielkości fotometryczne I Strumień świetlny (całoprzestrzenny) danego źródła światła opisuje ilość energii przenoszonej przez fale świetlne w jednostce czasu. Strumień jest podstawową wielkością fotometryczną – odpowiednikiem mocy. Strumień świetlny charakteryzuje przede wszystkim źródło światła, chociaż mówimy również o strumieniu odbitym. Światłość jest gęstością kątową strumienia świetlnego. Jednostką światłości jest kandela – należąca do siedmiu podstawowych jednostek miar.

---

Podstawowe wielkości fotometryczne II Luminancja jest najbliższa pojęciowo odczuciu intensywności światła spośród wielkości fotometrycznych. Odpowiada pojęciom jaskrawości (dla obiektów emitujących światło) i jasności (dla obiektów odbijających). Warto pamiętać, że odczucia jaskrawości lub jasności są wrażeniami bardzo subiektywnymi. Dodatkowo silnie zależą różnych czynników zewnętrznych np. od jasności tła na jakim jest obserwowany obiekt oraz od stanu adaptacji wzroku. Luminancja nie zależy od odległości od obiektu. Jeśli rozpatrzymy źródło światła i wszystkie parametry geometryczne są stałe, to luminancja źródła jest proporcjonalna do energii emitowanej przez źródło.

---

Podstawowe wielkości fotometryczne III Prawo Lamberta odnosi się także do odbicia światła od idealnie rozpraszającej powierzchni (powierzchni lambertowskiej). Powierzchnie rzeczywiste odbijają światło zgodnie z prawem Lamberta tylko w pewnym kącie. Dobrym przykładem materiału, którego powierzchnia odbija w przybliżeniu zgodnie z prawem Lamberta jest kreda.

---

Funkcja BRDF I Funkcję BRDF $f(\breve{L},\breve{V})$ definiuje się jako iloraz luminancji obserwowanej z kierunku $-\breve{V}$, do natężenia napromieniowania światła padającego z kierunku $-\breve{L}$. Znane funkcje BRDF można podzielić na dwie grupy : zależności opracowane eksperymentalnie i zależności mające podłoże fizyczne. Pierwszą grupę stanowią zależności, których opis matematyczny został eksperymentalnie dobrany do oczekiwanych (lub zmierzonych) efektów. Nie mają one żadnego uzasadnienia teorety¬cznego, ale są dobrą aproksymacją rzeczywistych zjawisk - dają dobre rezultaty. Drugą grupę stanowią opracowania, które powstały na podstawie odpowiedniej teorii fizycznej opisującej gładkość (chropowatość) powierzchni.

---

Funkcja BRDF II Symetryczność funkcji BRDF oznacza, że zamiana obserwatora i źródła światła nie spowodowałaby zmiany opisu zjawiska. To znaczy $f(\breve{L},\breve{V})=f(\breve{V},\breve{L})$. Drugim warunkiem jest zasada zachowania energii, zgodnie z którą suma całkowitej energii wypromieniowanej na skutek odbicia światła od powierzchni jest nie większa niż energia światła padającego.

---

Modele odbicia światła W literaturze można wskazać wiele prac porównujących, przede wszystkim pod względem obliczeniowym, różne podejścia do opisu zjawiska odbicia. Znane funkcje BRDF można podzielić na dwie grupy : zależności opracowane eksperymentalnie i zależności mające podłoże fizyczne. Pierwszą grupę stanowią zależności, których opis matematyczny został eksperymentalnie dobrany do oczekiwanych (lub zmierzonych) efektów. Nie mają one żadnego uzasadnienia teoretycznego, ale są dobrą aproksymacją rzeczywistych zjawisk. Drugą grupę stanowią opracowania, które powstały na podstawie odpowiedniej teorii fizycznej opisującej gładkość (chropowatość) powierzchni. Obie jednak grupy są pewnym przybliżeniem rzeczywistości. Natomiast ze względów praktycznych nie zawsze jest celowe korzystanie z funkcji BRDF powstałych na podstawie pomiarów rzeczywistej powierzchni, gdyż jest to bardzo kosztowne obliczeniowo. Nawet w takich przypadkach stosuje się pewne aproksymacje . Warto więc zastanowić się nad wyborem odpowiedniej funkcji BRDF. Szczególnie jest to istotne w sytuacji prowadzenia obliczeń z wykorzystaniem gotowych pakietów numerycznych gdzie wybór dostępnych parametrów może być ograniczony.

---

Model Cooka-Torrance’a (1981 r.) I Zaproponowany przez Cooka i Torrance’a w 1981 roku na podstawie wcześniejszych prac Torrance’a i Sparrowa. Model Cooka-Torrance’a jest modelem uzasadnionym fizycznie, spełniającym zasadę wzajemności i zasadę zachowania energii, chociaż znane są w literaturze rozważania wskazujące na pewne problemy, które mogą się pojawić dla kątów padania promienia bliskich kątowi prostemu. Znane jest również uproszczenie modelu Cooka-Torance’a - model Schlicka, zaproponowany w 1994 roku. Autor starał się dokonać uproszczenia z zachowaniem fizycznego charakteru modelu pierwotnego, ale znacznie podnieść atrakcyjność obliczeniową. W modelu Cooka-Torrance’a w równaniu zastąpione zostały wielkości G i D (funkcja rozkładu Beckmanna) prostszymi funkcjami wymiernymi.

---

Model Cooka-Torrance’a (1981 r.) II G opisuje tłumienie geometryczne. W modelu Cooka-Torrance’a założono, że powierzchnia materiału jest wielościanem złożonym z mikroelementów (mikroluster). Ich rozmiary i rozkład położeń decydują o chropowatości lub gładkości powierzchni. Przyjęto, że powierzchnia pokryta jest wgłębieniami typu V – to znaczy są to wgłębienia o kształcie ostrosłupa. Tłumienie geometryczne jest wzajemnym zasłanianiem mikroelementów powierzchni i jest opisane podaną zależnością.

---

Model Cooka-Torrance’a (1981 r.) III D jest funkcją rozkładu mikroelementów tworzących powierzchnię. Cook i Torrance zaproponowali użycie funkcji rozkładu Beckmanna jako najbardziej odpowiadającej wielościennemu charakterowi powierzchni dla różnych materiałów.

---

Funkcje rozkładu mikropowierzchni O właściwościach kierunkowego odbicia w przyjętym modelu decyduje funkcja D rozkładu mikropowierzchni (czasami nazywana funkcją dystrybucji). D jest najczęściej funkcją kąta $\beta$ (kąta $\alpha$ w przypadku modelu Phonga). Spełnienie zasady zachowania energii wymaga, aby funkcja dystrybucji spełniała warunek normalizacji. Oznacza to dla powierzchni izotropowych następującą zależność: $\underset{0}{\overset{\pi /2}{\int }}2\cdot D(\beta )\cdot cos\beta \cdot sin\beta \cdot d\beta =1$ Autorzy funkcji dystrybucji nie zawsze dbali o spełnienie tego warunku. Czasem dopiero niezależne prace późniejsze doprowadzały do spełnienia zasady zachowania energii – tak było np. w przypadku modelu odbicia Phonga. Aby móc porównywać różne funkcje dystrybucji, na rysunku są pokazane funkcje znormalizowane (oznaczone jako $\overline{D}$) tzn. takie, że $max(\overline{D})=1$. Oczywiście dla dowolnej funkcji dystrybucji jej maksimum występuje dla $\beta =0$. Istnieje wiele różnych funkcji dystrybucji. Ze względu na podobny charakter zmienności, Blinn sugerował możliwość zastąpienia jednej z nich drugą. Czasami może to być opłacalne obliczeniowo, jednak może powodować powstanie drobnych różnic na rysunku.

---

Współczynnik Fresnela Współczynnik Fresnela opisuje zależność odbicia światła od kąta padania i długości fali. Określa stosunek energii światła odbitego do energii światła padającego. Warto pamiętać, że kształt zależności kątowych tego współczynnika zależy od długości fali oraz polaryzacji światła. Prezentowane wykresy pokazują wartości średnie światła niespolaryzowanego. Schlick zaproponował dobrą aproksymację tej funkcji (według autora aproksymacji błąd mniejszy niż 1%). Opisuje ją wielomianowa funkcja kąta i wartość współczynnika $F_0$ dla zerowego kąta i określonej długości fali. Wartości $F_0$ są podawane przez tablice materiałowe.

---

Model Warda (1992 r.) Model Warda zaproponowany w 1992 roku uwzględniający anizotropię odbicia – równanie. Jest to jeden z pierwszych tego typu modeli i jednocześnie jest on często używany nadal. Model ten jest często dostępny w gotowych pakietach oprogramowania. Model Warda niestety nie uwzględnia współczynnika Fresnela, co nie daje możliwości opisania w pełni właściwości materiałowych i uwzględnienia zależności kątowych. Jest to szczególnie widoczne dla dużych kątów padania światła.

---

Model Orena i Nayara (1994 r.) Oren i Nayar zwrócili uwagę na rozkład postrzeganej luminancji na rzeczywistych powierzchniach rozpraszających. Zastosowanie modelu odbicia Lambertowskiego (opisu idealnego odbicia rozproszonego) powoduje. że efekt często całkowicie odbiega od rzeczywistego. Jest to spowodowane przede wszystkim rzeczywistym odbiciem rozproszonym, które odbiega od modelu Lambertowskiego. Rzeczywiste obiekty (np. porcelana nieszkliwiona) odbijają w taki sposób, że luminancja odbicia jest większa niż w modelu Lambertowskim. Oren i Nayar opracowali model, w którym przybliżyli powierzchnię obiektu powierzchnią wielościenną. Założyli, że obiekt pokryty jest wgłębieniami typu V podobnie jak w modelu Cooka-Torrance’a (i Sparrowa). Przy czy w modelu Orena i Nayara mikropowierzchnie nie są lustrzane ale rozpraszają w sposób lambertowski. To znaczy dla każdej pojedynczej mikropowierzchni jest stosowany Lambertowski model odbicia. Dla takiego modelu powierzchni zastosowali rozkład Gaussa kierunku wektora normalnego do powierzchni wielościennej. W efekcie uzyskali model uwzględniający wzajemne zasłanianie powierzchni wielościennej typu V ale przy lambertowskim odbiciu od mikropowierzchni. Ponieważ uzyskany opis był zbyt skomplikowany do zastosowań praktycznych, zaproponowali aproksymację prostymi równaniami.

---

Model Ashikhmina i Shirleya (2000r.) I Model Ashikhmina I Shirleya jest współczesnym modelem odbicia. Spełnia wszystkie podstawowe wymagania (zasada wzajemności, zasada zachowania energii, uwzględnia współczynnik Fresnela odbicia światła). Pozwala uwzględnić anizotropię odbicia. Został sformułowany w taki sposób, że może być wykorzystywany w dowolnych obliczeniach graficznych – także we wszystkich wariantach metody śledzenia promieni. (Model He nie może być wykorzystywany w algorytmach typu Monte Carlo.) Ma dodatkowo jeszcze jedną zaletę: jest modelem atrakcyjnym obliczeniowo.

---

Model Ashikhmina i Shirleya (2000 r.) II Model Ashikhmina I Shirleya opisuje także odbicie rozproszone. Pozwala je opisać w sposób bliższy zmianom rzeczywistym niż teoretyczny opis Lamberta. Jednocześnie trzeba podkreślić, że jest to inne podejście do opisu odbicia rozproszonego niż w modelu Orena i Nayara. W modelu Ashikhmina I Shirleya wykorzystano opis oparty na pomyśle Schlicka aproksymacji wielomianowej.

---

---

Porównanie właściwości Rysunek przedstawia zmianę kształtu funkcji odbicia w zależności od kąta padania światła dla przykładowych wartości parametrów. Aby możliwe było porównanie różnych modeli odbicia przeprowadzono przeliczenie parametrów między modelami w taki sposób, aby uzyskać zgodność dla kątów odpowiadających połowie wartości funkcji. – Takie postępowanie opisał Blinn w 1977 roku dla funkcji rozkładu mikropowierzchni. Jednocześnie dokonano normalizacji funkcji dla zerowego kąta padania światła. Dzięki temu możliwe staje się zastąpienie jednej funkcji drugą. Możliwe jest także porównanie kształtów – właściwości poszczególnych funkcji. Jak widać modele Cooka-Torrance’a, Ashikhmina-Shirleya, He-Torrance’a-Silliona-Greenberga i Warda wykazują zbliżone kształty funkcji BRDF dla różnych kątów padania światła. Przy czym zależności Warda dają inne proporcje zależności kątowych. Model ten nie uwzględnia współczynnika Fresnela. Stąd wartości maksymalne w opisie Warda odbiegają od wartości w modelach Cooka-Torrance’a, Ashikhmina-Shirleya, He-Torrance’a-Silliona-Greenberga. Jako punkt odniesienia przyjmuje się model He-Torrance’a-Silliona-Greenberga. Badania doświadczalne pokazały, że najlepiej opisuje on zachowanie rzeczywistych powierzchni. Niemniej jednak ze względu na złożoność obliczeniową i jednocześnie bardzo zbliżone właściwości (rysunek) modele Cooka-Torrance’a oraz Ashikhmina-Shirleya są atrakcyjniejsze. Warto pamiętać jednocześnie, że model He-Torrance’a-Silliona-Greenberga nie może być stosowany w odmianach metody śledzenia promieni, gdzie wymagana jest funkcja gęstości prawdopodobieństwa. Model Phonga nie pasuje do pozostałych, gdyż w ogóle nie uwzględniono w nim ani kąta padania, ani współczynnika Fresnela.

---

Inne sposoby opisu BRDF Modele analityczne zaprezentowane dotychczas są bardzo wygodne do zastosowań praktycznych, jednak często nie dają możliwości opisu skomplikowanej - rzeczywistej powierzchni odbijającej. Stosuje się kilka sposobów bardziej złożonych. Modele wielowarstwowe (np. model Hanrahana i Kreugera z 1993 roku). Wiele obiektów odbija światło wielowarstwowo. Z jednej strony materiały dielektryczne odbijają w sposób rozproszony dzięki tak zwanemu odbiciu objętościowemu. Światło wnika w materiał i po wielokrotnych odbiciach od cząstek materiału, część tego światła wychodzi na zewnątrz, tworząc składową rozproszoną odbicia. Z drugiej strony często mamy do czynienia z materiałami zbudowanymi z warstw o różnej przenikalności światła (i innych właściwościach odbiciowych). Dobrym przykładem jest skóra, której naturalna barwa jest bardzo trudna do uzyskania bez modeli wielowarstwowych. Do tego dochodzą materiały po prostu pokryte farbami lub innymi warstwami zmieniającymi właściwości odbiciowe. Zamiast próbować modelować skomplikowaną strukturę i właściwości powierzchni można zmierzyć właściwości odbiciowe i na tej podstawie zbudować tablicowaną funkcję BRDF. Oczywiście problem polega na tym, że żeby model pomiarowy był użyteczny to pomiary musza być dokonane z rozdzielczością wymaganą w obliczeniach związanych z danym obrazem i obiektem. Z drugiej strony wybrana próbka musi być reprezentatywna dla danego materiału. Jeżeli funkcję BRDF potraktować jako funkcję kątów w układzie sferycznym, to naturalnym sposobem opisu, będzie aproksymacja w postaci harmonicznych sferycznych (np. prace Westina z 1992 roku). Dzięki temu można rozłożyć opis odbicia na zestaw składowych, które mogą być używane z określoną dokładnością. Jeśli nie są potrzebne szczegóły powierzchni to można użyć prostszego zestawu opisu funkcji BRDF – bez składowych wyższych harmonicznych. Stosowane są również inne formy opisu aproksymacji: z wykorzystaniem wielomianów Zernike lub metodami falkowymi.

---

Problem cieniowania Wyznaczenie barwy związanej z modelem oświetlenia dla każdego punktu/piksela jest zadaniem kosztownym. Można zatem rozpatrywać cieniowanie (interpolację) które pozwoli wypełnić barwą wielokąty w sposób uproszczony. Stosuje się trzy warianty takiego wypełnienia – trzy warianty cieniowania. - Cieniowanie płaskie (cieniowanie stałą wartością), gdy cały wielokąt jest wypełniony taką samą barwa. - Cieniowanie Gouroud. - Cieniowanie Phonga. Cieniowanie płaskie jest zgodne z rzeczywistością, gdy obserwator lub źródło światła znajduje się w nieskończoności. Może być także stosowane, gdy wielokąt reprezentuje rzeczywiście powierzchnię modelowaną – mamy wtedy do czynienia z rzeczywistą powierzchnią wielościenną. Jeżeli jednak złożony kształt powierzchni obiektu jest przybliżony wielościanem, to można za pomocą cieniowania wygładzić obiekt niwelując wielościenny charakter.

---

Cieniowanie Gouraud Cieniowanie Gouraud jest procesem dwuetapowym: W pierwszym etapie wyznaczamy (hipotetyczną) barwę w wierzchołkach wielościanu. W tym celu wyznaczamy hipotetyczny wektor normalny jako średnią arytmetyczną wektorów normalnych wszystkich ścian, do których ten wierzchołek należy. Następnie na podstawie wektora normalnego wyznaczamy barwę wierzchołka korzystając z wybranego modelu odbicia światła. W drugim etapie dokonywana jest liniowa interpolacja barwy zgodnie z zaprezentowanymi wzorami.

---

Cieniowanie Phonga Cieniowanie Phonga polega na analogicznej interpolacji, tylko że nie barwy ale wektora normalnego. W pierwszym etapie wyznaczamy wektor normalny w wierzchołku w ten sam sposób jak w cieniowaniu Gouraud. W drugim etapie wyznaczamy interpolowany wektor normalny dla każdego piksela (to znaczy dla punktu powierzchni odpowiadającego pikselowi). Następnie wyznaczamy barwę piksela, na podstawie interpolowanego wektora normalnego korzystając z wybranego modelu odbicia światła.

---

Cieniowanie – interpolacja oświetlenia Porównując cieniowanie Gouraud i Phonga można wskazać właściwości każdego z nich. Obie metody zapewniają ciągłą zmianę barwy eliminując skokowe zmiany cieniowania płaskiego. Cieniowanie Gouraud nie daje możliwości powstania lokalnego ekstremum (np. rozbłysku światła) w ramach jednego elementu płaskiego. Powoduje to uśrednienie jasności na powierzchni obiektu. Cieniowanie Phonga nie ma tej wady. Interpolacja wektora oddaje poprawnie lokalne ekstrema również w ramach pojedynczego elementu płaskiego. Cieniowanie Gouraud dopuszcza, niestety, powstawanie pasm Macha. Wady tej jest praktycznie pozbawione cieniowanie Phonga. Wadą cieniowania Phonga jest fakt, że jest ono ponad dwukrotnie droższe obliczeniowo od cieniowania Gouraud.

---

Problemy cieniowania Obie metody przybliżają rzeczywisty rozkład barw. Powoduje to, powstawanie błędów w specyficznych sytuacjach. Obie metody są wrażliwe na orientację cieniowanego obiektu. Jeśli obiekt ma różne jasności w wierzchołkach i zostanie obrócony, to interpolacja da różne efekty w zależności od położenia obiektu. W obu metodach liczy się hipotetyczny wektor normalny w wierzchołku wielościanu na podstawie średniej arytmetycznej wektorów normalnych sąsiadujących ścian. Może to spowodować powstanie błędnie skierowanych wektorów interpolowanych. Na dolnym rysunku wektory interpolowane wewnętrznych ścian będą inaczej skierowane niż rzeczywiste wektory normalne. Dodatkowo powstaje nieoczekiwany wpływ ścian sąsiednich. Ruch jednaj ściany zewnętrznej spowoduje zmianę hipotetycznego wektora normalnego w wierzchołku (przez wpływ na średnią), a w konsekwencji tego zmianę wektora interpolowanego ściany wewnętrznej.

---

Szyba Model szyby jest przykładem wygodnego uproszczenia obliczeń barwy. Jeśli płyta jest cienka – to znaczy nie powoduje zauważalnego przesunięcia promienia świetlnego, to obliczenia można uprościć analizując tylko współczynnik przepuszczania.

---

---