GKIW Moduł 6a

Komputerowe wspomaganie projektowania jest dziedziną stosunkowo nową, ale szeroko wykorzystywaną przez różnych specjalistów. Różnorakie zastosowania wymagają definicji – opisu reprezentacji różnych obiektów. Z jednej strony typowe obiekty mechaniczne czy architektoniczne, z drugiej efekty specjalne filmów science fiction, gdzie jedynym ograniczeniem jest wyobraźnia twórców. Z drugiej strony systemy wspomagania projektowania dają dodatkowe możliwości wykonywania wielu obliczeń związanych bezpośrednio z dziedziną zastosowania – obliczeń konstrukcyjnych czy wytrzymałościowych. Oczywiście grafika komputerowa daje możliwość zobaczenia projektu – możliwość wizualizacji wyobrażeń projektanta. Niezbędne staje się narzędzie do modelowania kształtu – obiektu, powierzchni. Warto zwrócić uwagę na fakt, że użytkownicy takich systemów reprezentują różne poziomy przygotowania informatycznego. System modelowania powinien być więc prosty i efektywny, powinien dawać możliwość definicji kształtu za pomocą minimalnej liczby parametrów, a modyfikacja kształtu powinna dotyczyć wybranego fragmentu, a nie całości krzywej czy powierzchni.

---

W latach sześćdziesiątych XX wieku w fabryce Renault rozpoczął pracę pierwszy system modelowania geometrycznego na użytek komputerowego wspomagania projektowania. Twórcą tego systemu był P. Bézier – będący jedną z najważniejszych postaci w tej dziedzinie. Dzisiaj każda fabryka samochodów projektuje kształty karoserii wykorzystując modelowanie geometryczne. Istnieje wiele metod modelowania krzywych i powierzchni. Mają one różne właściwości i wymagają osobnego omówienia.

---

Wydawać by się mogło, że najprostszą forma modelowania krzywej jest wskazanie zbioru punktów na niej leżących a następnie połączenie ich krzywą interpolującą – najprościej wielomianową. Jeżeli dany jest ciąg parami różnych liczb Parser nie mógł rozpoznać (błąd składni): {\displaystyle t_0, t_1, t_2, …t_n } – węzłów interpolacyjnych i odpowiadających im punktom Parser nie mógł rozpoznać (błąd składni): {\displaystyle P_0, P_1, P_2,…P_n.} To poszukujemy krzywej wielomianowej P(t) takiej, że jest ona stopnia co najwyżej n oraz P(ti)=Pi dla każdego i. Tak sformułowane zadanie jest zadaniem interpolacyjnym Lagrange’a i ma dokładnie jedno rozwiązanie w postaci: $P(t)={\mathrm{\Sigma }}_{i=0}^n{P}_i(\prod _{j=0j\ne i}^n\frac{t-t_j}{t_i-t_j})$ Dla małej liczby punktów (kilku) uzyskana krzywa zachowuje się zgodnie z oczekiwaniem. Niestety dla większej liczby punktów – krzywa wykazuje bardzo dużą wrażliwość na zaburzenia węzłów i skłonność do oscylacji – co pokazuje rysunek a). Dodatkowo każdy fragment krzywej zależy od wszystkich węzłów – brak jest lokalnej reprezentacji. Problem oscylacji można rozwiązać korzystając z interpolacji krzywą sklejaną – przedziałami wielomianową niskiego stopnia, rysunek b). Jednak w obu przypadkach kontrola nad kształtem krzywej pomiędzy węzłami jest trudna. Wady te powodują, że takie rozwiązanie jest praktycznie nieprzydatne.

---

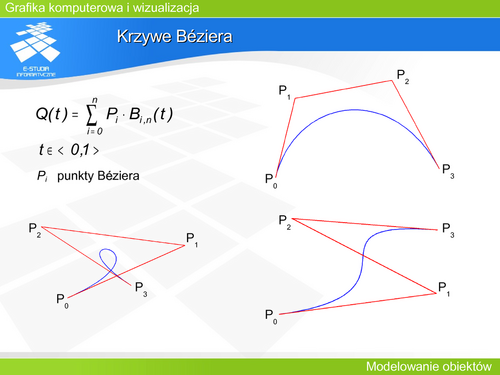
Wiele krzywych jest opisanych równaniem uwikłanym. Taka reprezentacja nie daje możliwości kontroli konkretnego fragmentu krzywej. Wygodnym sposobem opisu krzywych i powierzchni jest opis parametryczny. W tym przypadku za pomocą doboru wartości parametru można zdefiniować dowolny fragment krzywej, a kierunek wzrostu parametru jednoznacznie określa np. kierunki stycznych połączonych fragmentów. Przykładowa czterolistna koniczynka jest narysowana na rysunku a) w postaci rozety czterolistnej : $x(t)=a\cdot sin(1\cdot t)\cdot cos(t)$ $y(t)=a\cdot sin(1\cdot t)\cdot sin(t)$ dla $a>0,0<t<2\pi$ Na rysunku b) w postaci hipotrochoidy: $x(t)=(R+r)cos(t)-\lambda rcos(\frac{R+r}{r}t)$ $y(t)=(R+r)sin(t)-\lambda rsin(\frac{R+r}{r}t)$ dla $R>0,r<0,\lambda >1,0<t<2<2\pi$ Często wykorzystywanymi powierzchniami są powierzchnie drugiego stopnia. Ich równanie uwikłane ma postać: $f(x,y,z)=P^{T}QP=0$ gdzie Q jest macierzą współczynników postaci $Q=\left[\begin{array}{cccc}A& D& F& G\\ D& B& E& H\\ F& E& C& J\\ G& H& J& K\\ \end{array}\right]$

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---