GKIW Moduł 9

---

---

Definicja Modelowanie lokalnego odbicia (lub przenikania) światła nosi czasem nazwę problemu oświetlenia lokalnego. Uwzględnia bowiem tylko lokalne właściwości powierzchni. Problem oświetlenia globalnego jest natomiast opisem zależności związanych z rozchodzeniem się światła, ale uwzględniającym wzajemne oddziaływanie między powierzchniami – np. wielokrotne odbicie światła między różnymi przedmiotami. Próby rozwiązania tego problemu na poziomie modelu odbicia lokalnego sprowadzały się do uwzględnienia średniej wartości oświetlenia we wszystkich punktach sceny – oświetlenia tła. Taka składowa jest uwzględniona w modelu Phonga. W grafice komputerowej stosowane są dwie ogólne metody rozwiązania problemu oświetlenia globalnego: - Metoda śledzenia promieni, - Metoda bilansu energetycznego.

---

Generowanie próbek I Zastosowanie całkowania Monte Carlo wymaga wygenerowania próbek o określonym rozkładzie i w zdefiniowanym obszarze. Niestety programy biblioteczne najczęściej pozwalają uzyskać ciąg próbek pseudolosowych o rozkładzie równomiernym w obszarze prostokątnym jednostkowym. Generowanie wartości losowych zgodnie z zadanym rozkładem gęstości prawdopodobieństwa może być zrealizowane jedną ze znanych metod. Najczęściej stosuje się metodę funkcji odwrotnej do dystrybuanty lub metodę usuwania próbek niepasujących. Pierwsza metoda wymaga analitycznego wyznaczenia dystrybuanty na podstawie funkcji gęstości prawdopodobieństwa, a następnie wyznaczenia funkcji odwrotnej. Uzyskana funkcja przelicza próbki o rozkładzie równomiernym na próbki o zadanym rozkładzie. Metoda ta jest bardzo efektywna, ale nie zawsze możliwe jest wyznaczenie odpowiedniej funkcji odwrotnej.

---

Generowanie próbek II Dobrym przykładem wykorzystania metody funkcji odwrotnej do dystrybuanty jest wygenerowanie próbek o rozkładzie równomiernym w kole o zadanym promieniu. Wydawać by się mogło, że najprostszym rozwiązaniem takiego zadania będzie wygenerowanie próbek w prostokącie jednostkowym a następnie przeliczenie ich współrzędnych do współrzędnych biegunowych. Takie rozwiązanie nie daje rozkładu równomiernego w kole. Można to natomiast osiągnąć stosując metodę funkcji odwrotnej do dystrybuanty. Podane wzory pokazują przeliczenie współrzędnych z układu prostokątnego (gdzie są wygenerowane próbki pseudolosowe o rozkładzie równomiernym w prostokącie jednostkowym) na układ biegunowy koła, Takie przeliczenie zapewnia równomierność rozkładu próbek w kole.

---

Generowanie próbek III Metoda usuwania próbek niepasujących wymaga zdefiniowania obszaru (prostokąta) obejmującego zadany obszar i wygenerowania próbek o rozkładzie równomiernym. Oczywiście część z nich będzie poza zadanym obszarem – należy je odrzucić. Metoda ta może być praktycznie zawsze zastosowana – nie ma żadnych ograniczeń ani problemów analitycznych. Nie jest ona jednak efektywna, gdyż wymaga generowania dużej liczby próbek, które nie są potem wykorzystywane. Rysunek pokazuje zastosowanie tej metody do generowania próbek w kole, część próbek leżących poza obszarem koła zostaje odrzucona.

---

Śledzenie stochastyczne W śledzeniu stochastycznym generowanych jest wiele promieni (9, 16 lub nawet więcej) na piksel. Każdy z promieni może pójść własną drogą – to znaczy dla każdego będzie analizowane inne drzewo przecięć. Barwa piksela jest uśrednieniem tych promieni. Odbicie (załamanie) promienia trafiającego w powierzchnię obiektu zależy od funkcji BRDF traktowanej jako gęstość prawdopodobieństwa. Wygenerowanie promieni przechodzących przez piksel w sposób zdeterminowany w regularnej siatce powoduje powstanie takich samych zniekształceń intermodulacyjnych jak w klasycznym śledzeniu (efekt schodkowy, mory na obszarach pokrytych teksturą). Aby temu zaradzić można generować próbki losowo na obszarze piksela. Jednak w tym przypadku pojawia się bardzo silny szum nakładający się na wyznaczone barwy. Najlepszym rozwiązaniem byłoby wygenerowanie próbek w taki sposób, aby utrzymać między nimi pewną minimalną odległość. Spowodowałoby to znaczną redukcję amplitudy szumu. Niestety takie rozwiązanie jest zbyt kosztowne obliczeniowo. Dobrym kompromisem (i najczęściej stosowanym) jest generowanie próbek na regularnej siatce, ale z dodatkiem przypadkowych przesunięć (ang. jittering sampling lub stratified sampling). Jest to proste obliczeniowo i jednocześnie jeśli przesunięcia są nieskorelowane, to występuje znacząca redukcja szumu przy minimalnych zniekształceniach intermodulacyjnych. Zastosowanie próbkowania stochastycznego pozwala traktować wyznaczenie barwy piksela jako całkowanie po obszarze piksela. Dzięki temu możliwe jest uzyskanie miękkich cieni i rozmycia odbicia światła, możliwe jest uwzględnienie odbić nieidealnych kierunkowo i rozproszonych. Wadą takiego rozwiązania jest pojawiający się szum, który można redukować przez zwiększenie liczby promieni, co z kolei, niestety, pociąga za sobą zwiększenie czasu realizacji. Warto pamiętać, że dzisiaj przyjęło się, że jeśli występuje nazwa „metoda śledzenia promieni” bez dodatkowych określeń to jest to rozumiane właśnie jako śledzenie stochastyczne, a nie klasyczne Whitteda.

---

Mapowanie fotonowe I Etap1. Rozsyłanie fotonów. Na powierzchni źródła generowane są fotony, które są rozsyłane zgodnie z kierunkiem rozchodzenia się światła. Symuluje to emisję światła przez powierzchnię źródła. Ruch wyemitowanych fotonów odbywa się zgodnie z zasadami optyki geometrycznej. Zjawiska odbicia i przenikania (załamania) są opisane za pomocą odpowiednich modeli matematycznych (BRDF ). Każdy foton pokonuje pewną drogę napotykając na niej kolejne powierzchnie. Na każdej z nich, przy każdym odbiciu lub załamaniu, foton może pozostawić część swojego strumienia. W ten sposób z tych „pozostałości” powstaje mapa fotonowa. Struktura danych tej mapy obejmuje nie tylko wartość pozostawionego w danym punkcie strumienia, ale także parametry geometryczne – współrzędne punktu i kierunek padania fotonu. Etap2. Zbieranie fotonów. Aby stworzyć obraz, przez każdy piksel ekranu jest prowadzony promień zgodnie ze zdefiniowanym sposobem patrzenia przez obserwatora (zgodnie z odpowiednim rzutowaniem). Droga tego promienia jest następnie analizowana tak jak w klasycznym śledzeniu promieni. Luminancja danego piksela jest wyznaczana tak jak w śledzeniu stochastycznym, ale całkowaniu Monte Carlo podlegają zgromadzone na danej powierzchni fotony. Mapowanie fotonowe zostało stworzone jako mechanizm uzupełniający śledzenie promieni w celu symulacji zjawisk takich jak np., skupienie światła oraz uwzględnienie nieidealnych właściwości odbijających zarówno powierzchni rozpraszających jak i lustrzanych.

---

Mapowanie fotonowe II Przykłady obrazów wygenerowanych z wykorzystaniem mapowania fotonowego. Dzięki zastosowaniu tej techniki w metodzie śledzenia promieni możliwe stało się uzyskanie takich efektów jak rozproszenie światła za szklanką z płynem na lewym rysunku, oraz skupienia światła (caustic) na rysunku środkowym i prawym.

---

Metoda śledzenia promieni a CSG Warto zauważyć, że omawiana wcześniej metoda modelowania – konstrukcyjna geometria brył może być bezpośrednio połączona z metodą śledzenia promieni. Jeśli zachodzi pewien mechanizm operacji wolumetrycznej modelowania, na przykład określenie części wspólnej (iloczynu) obiektów A i B, to operacja ta również odnosi się do prostej będącej analizowanym promieniem w metodzie śledzenia. Przy czym odniesienie tego do promienia oznacza operację na odcinkach o końcach wyznaczonych przecięciem promienia z powierzchnią obiektów. Wyznaczenie operacji wolumetrycznych odcinków na prostej jest zadaniem bardzo prostym. W takim razie nie jest w ogóle potrzebne niezależne wyznaczanie powierzchni będących rezultatem operacji wolumetrycznych. Można to zrobić podczas rysowania obrazu. Wystarczy, że analizując przecięcia dla każdego promienia zostanie uwzględniony mechanizm modelowania obiektu metodą konstrukcyjnej geometrii brył i wyznaczone odpowiednie punkty przecięć.

---

Algorytmy przyspieszające śledzenie promieni I Barwa każdego piksela obrazu jest wyznaczana w podobny sposób przez analizę odpowiedniego drzewa przecięć. Liczba operacji z tym związanych rzutuje na czas obliczeń całości. Z drugiej strony można wskazać operacje, które pojawiają się najczęściej – są to z reguły operacje związane z szukaniem przecięcia promienia z powierzchnią obiektu. Stąd algorytmy przyspieszające metodę śledzenia próbują zredukować koszty obliczeń albo przez przyspieszenie wyznaczania przecięć, albo przez zmniejszenie nakładu pracy związanej z analizą drzewa.

---

Algorytmy przyspieszające śledzenie promieni II Metody te koncentrują się z jednej strony na operacjach numerycznych, a z drugiej na technice wyboru promieni do analizy. Stosowane operacje matematyczne i uproszczenia opisu mają na celu wyłącznie zmniejszenie powtarzanych obliczeń. Odbywa się to przez wyznaczenie wartości pewnych wyrażeń (wybierane są takie wyrażenia, których wartości są niezależne od równania promienia) w preprocesingu przed analizą biegu promienia. Wyniki tych obliczeń są później wykorzystywane w trakcie śledzenia promieni. Dzięki temu unika się wielokrotnego powtarzania tych samych operacji matematycznych. Oczywiście możliwość optymalizacji tą drogą wymaga dość żmudnej analizy równań powierzchni, a efektywność przyspieszenia bardzo ściśle zależy od opisu powierzchni. Nie prowadzi to natomiast do przybliżenia ani zmiany wartości obliczeń końcowych.

---

Algorytmy przyspieszające śledzenie promieni III Stwierdzenie czy promień przecina dany obiekt jest zadaniem trudnym. Zastosowanie odpowiedniej techniki wyboru promieni, które mają szansę na przecięcie, pozwala wyeliminować zbędne przypadki, dla których nie trzeba przeprowadzać długiej i kosztownej, pełnej analizy biegu promienia. Techniki wyboru promieni można podzielić na dwie grupy: zastosowanie brył otaczających i podział przestrzeni. W pierwszym przypadku (bryły otaczające) zanim rozpocznie się wyznaczanie przecięcia promienia z powierzchnią obiektu, można spróbować wyznaczyć przecięcie z bryłą otaczającą obiekt. Jeśli promień nie przecina takiej bryły, to analiza przecięcia z obiektem nie jest konieczna. Oczywiście aby w takiej sytuacji można było mówić o przyspieszeniu obliczeń powinny być spełnione dwa warunki. Bryła powinna „ściśle” (ciasno) otaczać obiekt oraz wyznaczenie przecięcia promienia z bryłą powinno być wielokrotnie prostsze (i szybsze) niż przecięcia z obiektem. Często te warunki są sprzeczne. Najczęściej stosuje się kule, wielościany lub „pasy” równoległych płaszczyzn jako bryły otaczające. Kula jest obiektem, dla której najszybciej można stwierdzić, czy jest przecięta prostą czy nie. Wystarczy znaleźć odległość prostej od środka kuli i porównać z promieniem. Jest to szybsze niż sprawdzanie przecięcia prostej z prostopadłościanem. Wadą kuli jako obiektu otaczającego jest najczęściej niezbyt ciasne obejmowanie obiektu. Warto zwrócić uwagę na przecięcia z obiektami typu AABB (ang. Axis-Aligned Bounding Box - prostopadłościan o krawędziach wyznaczonych przez proste równoległe do osi układu współrzędnych) i OBB (ang. Oriented Bounding Box - prostopadłościan dowolnie zorientowany) Aby zwiększyć efektywność działania metody można skonstruować hierarchię brył otaczających.

---

Ogólne równanie renderingu Kajiya Transport światła odbywa się na scenie na drodze wielokrotnych odbić od poszczególnych fragmentów powierzchni. Ogólne równanie renderingu opisuje zależność między oświetleniem wzajemnym elementarnych fragmentów powierzchni. Rozpatrując dwa fragmenty $x$ i $x^{\prime }$ określamy transport od $x^{\prime }$ do $x$. Równanie uwzględnia przy tym zarówno emisję własną fragmentu $x^{\prime }$ jak i odbicie przez $x^{\prime }$. Takie sformułowanie daje możliwość zbudowania zależności rekurencyjnej między wszystkimi fragmentami sceny. Z drugiej strony jeśli podzielić całą scenę na fragmenty elementarne, to uwzględnienie równania renderingu wymaga analizy „każdy z każdym” tych fragmentów. Prowadzi to oczywiście do złożoności kwadratowej problemu oświetlenia globalnego. Równanie wizualizacji zaproponowane przez Kajiya z 1986 roku pozwala prześledzić rekurencyjnie drogę promieni i wyznaczyć intensywności oświetlenia określonych powierzchni. Uwzględnienie wielkości świetlnych doprowadziło do powstania luminancyjnego równania wizualizacji opisywanego przez Cohena w 1993. Pozwala prowadzić obliczenia w grafice komputerowej z uwzględnieniem zasad fizyki. Po uwzględnieniu wielkości świetlnych luminancyjne równanie wizualizacji wyznacza rozkład luminancji.

---

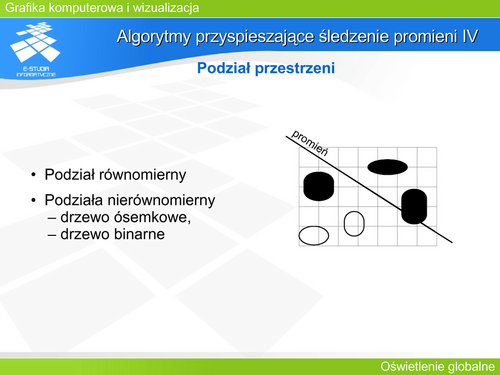
Algorytmy przyspieszające śledzenie promieni IV Niejako odwrotne podejście do problemu w stosunku do hierarchii brył otaczających stanowi podział przestrzeni. W tym przypadku całą przestrzeń sceny dzieli się na prostopadłościenne sektory. Następnie zamiast otaczać obiekt przyporządkowuje się mu odpowiedni sektor (sektory), w którym obiekt się znajduje. Dzięki temu analizując drogę promienia przez kolejne fragmenty przestrzeni można sprawnie wybrać obiekty, które w nich się znajdują. Stosuje się podział równomierny lub nierównomierny. W tym drugim przypadku jest podział hierarchiczny: drzewo ósemkowe lub binarne.

---

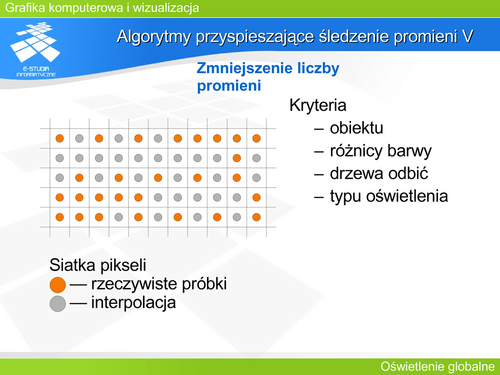
Algorytmy przyspieszające śledzenie promieni V Wyróżnia się dwa przypadki. Zmniejszenie liczby promieni pierwotnych i/lub zmniejszenie liczby promieni wtórnych. W pierwszym przypadku zakłada się, że barwa i intensywność sąsiednich pikseli są zbliżone. Można więc przeprowadzić dokładne obliczenia dla mniejszej rozdzielczości rastra niż w rzeczywistości (np. dla co czwartego piksela), natomiast pozostałe piksele wyznaczyć dokonując interpolacji. Oczywiście warto zastosować mechanizm adaptacyjny. Przyjąć maksymalną różnicę wartości, która dopuszcza interpolację – przekroczenie jej spowoduje wyznaczenie wartości piksela po przeprowadzeniu dokładnych obliczeń, a nie w wyniku interpolacji. W drugim przypadku dla każdego piksela zmniejsza się głębokość drzewa kolejnych przecięć lub odbić, dzięki czemu nie są brane pod uwagę kolejne promienie. Pominięcie niektórych pikseli lub zmniejszenie rozdzielczości rastra oznacza po prostu zmniejszenie dokładności wyznaczenia rozkładu oświetlenia. Podobny problem powstanie w przypadku nadpróbkowania. Jeśli jest ono stosowane, to liczba próbek na piksel wynika z założonej dokładności obliczeń i rezygnacja nawet adaptacyjna z pewnej liczby próbek pogarsza tę dokładność. Przy wykorzystaniu metody adaptacyjnej redukcji promieni pierwotnych w typowych zastosowaniach metody śledzenia często oprócz wspomnianego warunku wartości progowej uwzględnia się kilka innych wymaganych do skorzystania z interpolacji.: Warunek wspólnego drzewa odbić: dopuszcza się interpolację, jeśli promienie, które mają służyć do wyznaczenia podstawy do interpolacji, mają to samo (lub podobne) drzewo przecięć. Warunek wspólnego obiektu: dopuszcza się interpolację, jeśli promienie pierwotne trafiają w ten sam obiekt. Warunek cienia/oświetlenia: dopuszcza się interpolację, gdy oba piksele mające być podstawą interpolacji, są albo oświetlone, albo w cieniu. Metoda jest bardzo atrakcyjna obliczeniowo, jednak może pogarszać jakość końcową. Dobór właściwie zastosowanych kryteriów korzystania z interpolacji powinien zapewnić kompromis dający niewidoczne spadki jakości przy zauważalnej redukcji czasu obliczeń.

---

Algorytmy przyspieszające śledzenie promieni VI Metody analizy gęstości zakładają, że jeśli promień trafi, na drodze do źródła światła, w obszar w którym znajduje się odpowiednio duża liczba obiektów („gęstość” powyżej pewnego progu), to zostanie on zatrzymany i do tego źródła nie dotrze. Można tak przyjąć z dużym prawdopodobieństwem, bez analizy przecięć z konkretnymi obiektami z tego obszaru. Takie postępowanie czasami prowadzi do błędów, które wprawdzie nie przeszkadzają w odbiorze filmów czy reklam, ale mogą zafałszować obraz rozkładu oświetlenia. Problemu tego nie stwarzają metody zmniejszające głębokość drzewa promieni wtórnych po znalezieniu obiektu zasłaniającego źródło światła. Przy analizie oświetlenia złożonych elementów, przy dużej liczbie obiektów i jednocześnie dużej liczbie źródeł światła powstaną strefy cienia dające możliwość redukcji obliczeń tą metodą.

---

Algorytmy przyspieszające śledzenie promieni VII Proces obliczeniowy dla pojedynczego piksela jest praktycznie niezależny od obliczeń związanych z sąsiednimi pikselami. Teoretycznie więc, każdy piksel mógłby być liczony przez niezależny komputer, a potem z gotowych pikseli można byłoby złożyć obraz. W praktyce bardzo rzadko zdarza się możliwość dysponowania tak dużą liczbą jednostek obliczeniowych. Można więc, podzielić obraz na dowolne fragmenty i rozdzielić je pomiędzy jednostki obliczeniowe maszyny równoległej. Podczas produkcji filmów wykorzystuje się możliwość niezależnego, równoległego wyznaczania całych obrazów, np. kolejnych klatek filmu lub możliwość innego rozłożenia filmu na obrazu lub fragmenty do równoległej obróbki. Wymaga to oczywiście udziału wielu komputerów lub specjalizowanego sprzętu wieloprocesorowego.

---

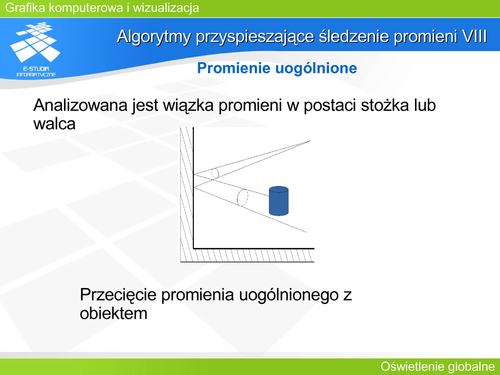
Algorytmy przyspieszające śledzenie promieni VIII Technika ta jest stosunkowo rzadko wykorzystywana. Chociaż analiza wiązek promieni może być zgodna z oczekiwaniem wyznaczenia kierunków, z jakich cały obiekt jest oświetlony przez dane źródło. A zatem teoretycznie byłoby to pomocne np. gdy na scenie znajduje się wiele przedmiotów i oświetlone są one kilkoma źródłami światła. Jednak teoretyczne korzyści metody wiążą się niestety z wieloma problemami pojawiającymi się w praktycznych zastosowaniach.

---

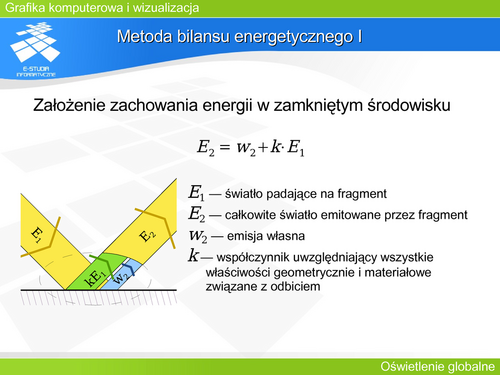
Metoda bilansu energetycznego I Metoda energetyczna (ang. radiosity), rozwinęła się na bazie metody elementu skończonego (MES) oraz na doświadczeniach jej wykorzystywania w technice cieplnej do opisu emisji i odbicia promieniowania cieplnego. Realizacja metody energetycznej wymaga podziału wszystkich powierzchni w rozpatrywanym układzie optycznym na elementarne fragmenty, dla których bazując na zasadzie zachowania energii w zamkniętym środowisku tego fragmentu, można opisać równaniem transportu promieniowania. Przyjmuje się, że elementarne fragmenty mają skończone rozmiary, są płaskie i wszystkie podlegają tym samym regułom emisji, odbicia, przenikania lub absorpcji promieniowania. Przyjmuje się, że pojedynczy fragment odbija światło w sposób równomiernie rozproszony. Pomiędzy dowolną parą elementarnych fragmentów zachodzą zjawiska związane z transportem światła. Metoda bilansu energetycznego pojawiła się w literaturze dotyczącej grafiki komputerowej w latach 1984-1985. Wśród autorów należy wymienić Gorala, Cohena Greenberga, Nishitę i Nakamaego.

---

Metoda bilansu energetycznego II Metoda energetyczna umożliwia przeprowadzenie przede wszystkim analizy zjawisk rozproszonych. O wiele trudniejszym do opisu jest odbicie kierunkowo-rozproszone. Natomiast założenie odbicia rozproszonego przez elementarne fragmenty praktycznie wyklucza analizę odbić kierunkowych na scenie. Cechą charakterystyczną metody energetycznej jest fakt, że w opisach transportu nie występuje obserwator (co tak naprawdę jest zgodne z rzeczywistością – światło rozchodzi się bez względu na to czy obserwator będzie brał w tym udział czy nie). Obserwator zostaje uwzględniony dopiero w fazie wizualizacji. Oznacza to, że do przeprowadzenia generacji obrazu metodą bilansu energetycznego i tak na końcu trzeba uruchomić metodę śledzenia promieni w najprostszej postaci.

---

Równanie bilansu energetycznego Każda powierzchnia elementarna odbija i emituje światło równomiernie we wszystkich kierunkach. Równanie bilansu energetycznego jest więc równaniem bezkierunkowym. Współczynniki odbicia danego fragmentu również są wielkościami bezkierunkowymi i określają tylko proporcje. Współczynnik sprzężenia optycznego uwzględnia kształty i relatywne orientacje powierzchni. Dodatkowo należy uwzględnić długości fali. emitowanej w ramach emisji własnej powierzchni oraz fakt, że współczynnik odbicia może być również zależny od długości fali. W praktyce najczęściej prowadzi się obliczenia dla składowych r,g,b.

---

Współczynnik sprzężenia I Współczynnik sprzężenia nie jest zależny od obserwatora, jest zależny natomiast od właściwości powierzchni obiektów i ich wzajemnego ustawienia. Powinien być wyznaczony dla każdej pary powierzchni przed przystąpieniem do rozwiązywania układu równań bilansu energetycznego. Współczynnik sprzężenia optycznego jest większy od zera jeśli powierzchnie „widzą się”, lub jest zerem gdy powierzchnie „nie widzą się”.

---

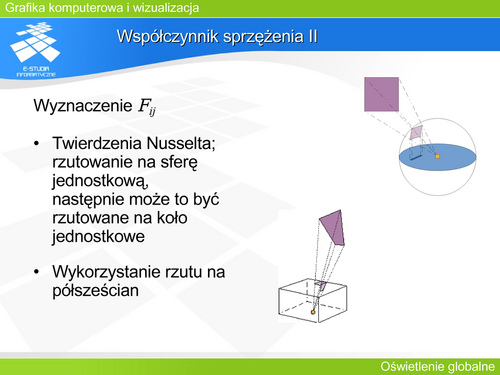
Współczynnik sprzężenia II Nusselt zauważył, że jeśli element i zostanie otoczony półsferą i dokonamy rzutu elementu j na tę półsferę, to z punktu widzenia oddziaływania w postaci współczynnika sprzężenia, obiekt j oraz jego rzut są równoważne. To znaczy że obiekty mające taki sam rzut na półsferę maja takie same współczynniki sprzężenia. Jeśli półsfera byłaby otoczona półsześcianem, to rzut na półsześcian tego samego obiektu byłby równoważny jego rzutowi na półsferę. W praktyce rzut na półsześcian okazał się najefektywniejszy obliczeniowo. Półsześcian dzieli się na powierzchnie elementarne (prostokątne piksele) i wyznacza współczynnik sprzężenia na podstawie rzutu obiektu na mapę pikseli półsześcianu.

---

Typy odbić wzajemnych Dobrą klasyfikacją zachowania się algorytmów oświetlenia globalnego jest klasyfikacja pokazująca w jaki sposób są implementowane wzajemne odbicia między dwiema powierzchniami. Biorąc pod uwagę dwa rodzaje odbicia: rozproszone i kierunkowe, możemy mieć do czynienia z czterema możliwościami odbić wzajemnych. Kierunkowe-kierunkowe – jest to implementowane przez klasyczną metodę śledzenia promieni (Whitteda). I praktycznie metoda klasyczna śledzenia nie pozwala na opis innych odbić wzajemnych. Rozproszone-rozproszone – jest to implementowane przez klasyczną metodę energetyczną. Podobnie jak śledzenie, klasyczna metoda energetyczna nie pozwalana na implementację innych wariantów odbić. Rozproszone-kierunkowe (także kierunkowe-rozproszone) – może być implementowane w nowszych rozwiązaniach metody śledzenia.

---

---

---

---

---

---

---

Metoda śledzenia promieni I Traktując model kamery jako mechanizm realizacji rzutowania perspektywicznego, można zauważyć, że barwa danego piksela ekranu powstaje dzięki światłu docierającemu do niego z kierunku wynikającego z rzutowania. Można zatem prześledzić „drogę światła”, które dociera do piksela i na tej podstawie wyznaczyć barwę. Metoda śledzenia promieni polega na analizie przebiegu promieni między obserwatorem a źródłem światła. Drogę promieni opisuje drzewo przecięć, którego węzły reprezentują zjawiska jakie zachodzą między promieniem a powierzchniami obiektów. Korzeń drzewa odpowiada promieniowi docierającemu do obserwatora zaś liście — źródłom światła. Zjawiska odbicia, przenikania i pochłaniania opisane są odpowiednimi modelami matematycznymi. Wyznaczenie barwy danego piksela polega na analizie odpowiedniego drzewa.

---

Metoda śledzenia promieni II Analizę „drogi światła” prowadzi się od obserwatora (kamery – środka rzutowania) do obiektów na scenie – to znaczy w kierunku przeciwnym do rzeczywistego rozchodzenia się światła. Stąd czasami metodę nazywa się metodą (śledzenia) promienia odwrotnego. Każde napotkanie obiektu przez promień (promień pierwotny) wymaga analizy. Zawsze jest wyznaczany promień odbity o kierunku zależnym od powierzchni obiektu. Jeśli obiekt jest przezroczysty, to wyznaczany jest promień załamany (promień przechodzący przez obiekt) o kierunku zależnym od właściwości materiałowych obiektu. Oba promienie: odbity i załamany nazywane są promieniami wtórnymi. Zawsze są również wyznaczane tak zwane promienie cienia (czasami nazywane promieniami oświetlenia) w kierunku każdego źródła światła. Promienie cienia pozwalają wyznaczyć oświetlenie danego elementu obiektu przez źródła światła, oczywiście jeśli na drodze promienia cienia do źródła światła jest inny obiekt nieprzezroczysty (źródło jest zasłonięte) to oświetlenie nie jest liczone. Promienie wtórne mogą wskazać następne przecięcia z obiektami, stając się wtedy promieniami pierwotnymi kolejnej analizy. Tak stworzone drzewo promieni jest obliczane metodą zstępującą, Barwa każdego węzła jest liczona jako funkcja barwy potomków. Gałąź w takim drzewie kończy się, gdy promienie wtórne (odbite i załamane) nie przecinają się z kolejnymi obiektami. Możne też być stosowane inne zakończenie procesu budowy i/lub analizy drzewa: gdy osiągnięto określony/zadany poziom rekurencji, albo po prostu gdy zabrakło pamięci na następne poziomy.

---

Metoda śledzenia promieni III Istnieje kilka różnych wersji realizacji tego algorytmu: - Śledzenie klasyczne (Whitteda), polegające na analizie pojedynczego promienia poczynając od obserwatora - odwrotnie niż rzeczywiste rozchodzenie się światła, - Śledzenie stochastyczne, kiedy promienie wysyłane są na zasadzie próbkowania pewnego obszaru, również odbicie (załamanie) światła jest modelowane na zasadzie funkcji prawdopodobieństwa, która określa w którym kierunku odbije się (załamie) promień. - Śledzenie dwukierunkowe, kiedy analiza jest przeprowadzana w obu kierunkach: poczynając od obserwatora i poczynając od źródła światła. - Mapowanie fotonowe (Jensena) jest śledzeniem dwukierunkowym rozszerzonym o tworzenie pośrednich źródeł światła na powierzchniach rozpraszających. Rozwój możliwości metody śledzenia promieni polega na dodawaniu coraz bardziej skomplikowanych przypadków, które mogą się pojawić na drodze promienia pomiędzy źródłem a obserwatorem. Najprościej jest opisać przebieg odbicia kierunkowego (lustrzanego), najtrudniej wielokrotne odbicie rozproszone i pośrednie oddziaływania typu składowej kierunkowej padającej na powierzchnię rozpraszającą.

---

Śledzenie klasyczne (Whitteda) Śledzenie klasyczne (Whitteda) odpowiada dokładnie opisanemu procesowi budowy i analizy drzewa promieni. Warto zauważyć, że opisany sposób analizy drzewa promieni odpowiada tak naprawdę kierunkowemu rozchodzeniu się światła. Oznacza to, że dobre efekty takiej analizy uzyskać można dla obiektów, które charakteryzują się właśnie kierunkowym charakterem odbicia i przenikania. Pierwsze rysunki wygenerowane przez Whitteda wzbudziły podziw gdyż pokazywały w sposób perfekcyjny załamanie światła przez sferyczne szklane obiekty. Podstawowym problemem śledzenia klasycznego ( i tak naprawdę każdej późniejszej modyfikacji metody) jest szybkie wyznaczenie przecięcia promienia z obiektem.

---

Rzeczywiste (niepunktowe) źródło światła Problem z opisem rzeczywistych obiektów za pomocą klasycznego śledzenia Whitteda zaczyna się pojawiać gdy weźmiemy pod uwagę rzeczywiste źródło światła (o skończonych – niepomijalnych rozmiarach). Analiza oświetlenia na drodze jednego promienia przestaje odpowiadać rzeczywistości. Osiągnięcie obrazu miękkiego półcienia jest całkowicie niemożliwe. Rozpatrując fragment powierzchni oświetlony bezpośrednio przez źródło powierzchniowe i biorąc pod uwagę równanie wizualizacji Kajiya, można wykazać, że luminancja $Lx(\breve{V})$ postrzegana na powierzchni $x$ z kierunku wektora $\breve{V}$ będzie opisana przedstawionym równaniem. Poprawny wynik może dać tylko analiza uwzględniająca całkowanie powierzchni źródła światła. Przykładem dobrej aproksymacji przy wykorzystaniu klasycznej metody śledzenia jest model Verbecka i Greenberga z 1984 roku. Zakłada on, że źródło powierzchniowe jest przybliżone zbiorem źródeł punktowych rozłożonych na powierzchni źródła.

---

Całkowanie Monte Carlo Rozwiązanie analityczne równania renderingu praktycznie nie ma sensu. Autorzy publikacji dotyczących tego tematu czasami sugerują możliwość rozwiązania analitycznego dla wybranego; wydzielonego i wyizolowanego problemu obejmującego na przykład pojedyncze elementy odbijające i jedno źródło światła o prostym opisie geometrycznym. Dla bardziej skomplikowanych scen trudności pojawiają się już na etapie opisu wzajemnego zasłaniania i kształtu jednego elementu widzianego z powierzchni drugiego. Dobrym rozwiązanie w takiej sytuacji – rozwiązaniem uniwersalnym jest zastosowanie całkowania Monte Carlo. Na przykład dla problemu pojedynczego powierzchniowego źródła światła można wygenerować zbiór promieni biegnących w kierunku odwrotnym od obserwatora do powierzchni i dalej odbijających się zgodnie z pewnym prawdopodobieństwem zależnym od właściwości odbiciowych powierzchni. Promienie odbite trafią (lub nie) w określony punkt powierzchni źródła, z którym to punktem będzie związana określona luminancja i barwa. Jeśli na podstawie analizy zachowania się takich promieni wyznaczymy wartość luminancji postrzeganej przez obserwatora to zadanie jest rozwiązane. Taką właśnie możliwość daje w tym przypadku całkowanie Monte Carlo. W najprostszym przypadku jednowymiarowym, jeśli chcemy obliczyć całkę $I=\underset{0}{\overset{1}{\int }}h(y)dy$ to możemy skorzystać z N liczb losowych o rozkładzie równomiernym $x_1,x_2,,,,x_N$, stanowiących pewną realizację zmiennej losowej $X$. Wtedy $I\approx \frac{1}{N}\sum _{i=1}^{N}h(x_i)$ Oczywiście takie proste całkowanie nie byłoby przydatne, gdyż w praktyce problem zachodzi w pewnym przedziale $S$ i jednocześnie wymagane jest losowanie próbek o rozkładzie innym niż równomierny. Podane wzory określają takie rozwiązanie. Warto zwrócić uwagę na zależności dotyczące błędu estymacji całki metodą Monte Carlo. Można pokazać, że wariancja estymacji jest proporcjonalna do $\frac{1}{\sqrt{N}}$ natomiast odchylenie standardowe do $\frac{1}{\sqrt{N}}$. W związku z tym, jeśli chcemy zmniejszyć błąd o połowę to $N$ musi wzrosnąć czterokrotnie.

---